|
Упражнение 2.1.25 |
Алгоритмические проблемы
14.3. Массовые задачи
Определение 14.3.1. Массовой задачей (problem) называется бесконечная серия "однотипных" индивидуальных задач (instance), каждая из которых имеет определенный ответ. С каждой массовой задачей связана некоторая фиксированная схема кодирования (encoding scheme), которая отображает индивидуальные задачи в их коды - слова в некотором фиксированном алфавите. При этом требуется, чтобы множество кодов всех индивидуальных задач было разрешимым.
Определение 14.3.2. Задачей распознавания (decision problem) называется массовая задача, в которой ответами индивидуальных задач могут быть только "да" и "нет" (то есть существует только два возможных ответа).
Пример 14.3.3.
Зафиксируем некоторый алфавит 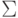 .
Рассмотрим следующие однотипные индивидуальные задачи:
даны два слова
.
Рассмотрим следующие однотипные индивидуальные задачи:
даны два слова 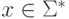 и
и  ,
необходимо выяснить, является ли
слово x
подсловом слова y.
,
необходимо выяснить, является ли
слово x
подсловом слова y.
Пусть # -
новый символ, не принадлежащий алфавиту 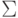 .
Кодом индивидуальной задачи про конкретные
слова x и y
будем считать слово x#y
в алфавите
.
Кодом индивидуальной задачи про конкретные
слова x и y
будем считать слово x#y
в алфавите  .
.
Эта массовая задача является задачей распознавания.
Определение 14.3.4. Алгоритмическая проблема - проблема, в которой требуется найти алгоритм для решения массовой задачи. Если такой алгоритм существует, то данная проблема называется алгоритмически разрешимой или просто разрешимой (decidable, solvable), в противном случае ее называют алгоритмически неразрешимой (undecidable, unsolvable).
Замечание 14.3.5. Алгоритмическая проблема, относящаяся к некоторой задаче распознавания, алгоритмически разрешима тогда и только тогда, когда разрешимо множество кодов индивидуальных задач с ответом "да".
Пример 14.3.6.
Рассмотрим массовую задачу из примера 14.3.3.
Соответствующая алгоритмическая проблема
разрешима, так как разрешим язык 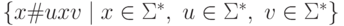 .
.
Пример 14.3.7.
Зафиксируем некоторый алфавит 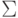 .
Рассмотрим следующие однотипные индивидуальные задачи:
дана порождающая грамматика
.
Рассмотрим следующие однотипные индивидуальные задачи:
дана порождающая грамматика
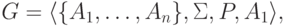
Для полной строгости необходимо договориться, как
кодировать грамматику G
в виде слова.
Например, можно использовать алфавит 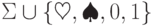 ,
где
,
где  -
дополнительные символы, не принадлежащие множеству
-
дополнительные символы, не принадлежащие множеству 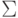 .
Вспомогательный символ Ai
заменим на слово, состоящее из
символа
.
Вспомогательный символ Ai
заменим на слово, состоящее из
символа  и кода числа i
в двоичной системе счисления.
В каждом правиле
и кода числа i
в двоичной системе счисления.
В каждом правиле  добавим символ
добавим символ  на месте
на месте 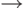 и после слова
и после слова 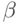 .
Кодом грамматики G
будем считать результат конкатенации кодов всех правил
из множества P.
Например, грамматика
.
Кодом грамматики G
будем считать результат конкатенации кодов всех правил
из множества P.
Например, грамматика
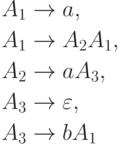
 )
кодируется словом
)
кодируется словом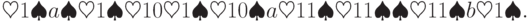
Легко понять, что соответствующая алгоритмическая проблема (проблема проверки праволинейности) разрешима.
Упражнение 14.3.8. Разрешима ли алгоритмическая проблема распознавания четности длины слова над алфавитом {a,b}?
14.4*. Грамматики типа 0
Теорема 14.4.1. Класс языков, порождаемых грамматиками типа 0, совпадает с классом перечислимых языков.
Доказательство можно найти, например, в [СерГал с. 24-26].
Упражнение 14.4.2. Выводимо ли слово aab в грамматике
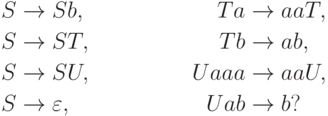
Упражнение 14.4.3. Выводимо ли слово aaaaaaaab в грамматике
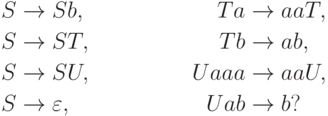
Замечание 14.4.4. Неизвестно, порождает ли грамматика
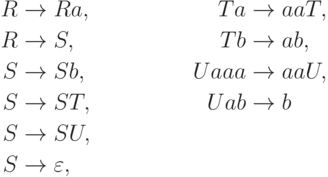
Упражнение 14.4.5.
Пусть 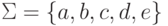 .
Рассмотрим грамматику
.
Рассмотрим грамматику

Упражнение 14.4.6. Является ли разрешимым язык, порождаемый грамматикой
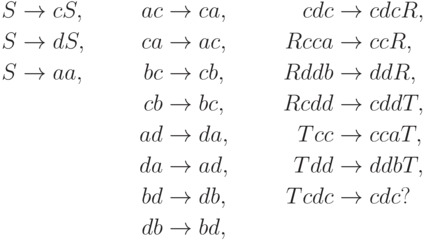
Определение 14.4.7. Порождающая грамматика в нормальной форме -
это порождающая грамматика, в которой
каждое правило имеет вид 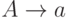 ,
, 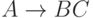 или
или 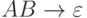 ,
где
,
где 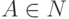 ,
, 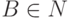 ,
, 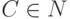 ,
, 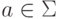 .
.
Теорема 14.4.8. Каждая порождающая грамматика эквивалентна некоторой порождающей грамматике в нормальной форме.
Упражнение 14.4.9.
Существует ли такая порождающая грамматика G,
что язык  не порождается ни одной грамматикой типа 0?
не порождается ни одной грамматикой типа 0?
