|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Минимаксные критерии для задач с неизвестным априорным распределением
Рассмотрим случай, когда статистик руководствуется оценкой априорного
распределения (17.6), задаваемой вероятностью 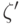 из
некоторого подынтервала
из
некоторого подынтервала 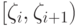 . Если при этом истинному распределению
соответствует значение
. Если при этом истинному распределению
соответствует значение 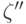 из того же подинтервала
из того же подинтервала 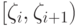 ,
то ожидаемые потери
,
то ожидаемые потери 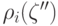 , определяемые
функцией (18.26),
совпадают с байесовским
риском, поскольку значениям
, определяемые
функцией (18.26),
совпадают с байесовским
риском, поскольку значениям 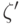 и
и 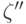 соответствует одна и та же критическая
область Q1(i) из (18.17).
соответствует одна и та же критическая
область Q1(i) из (18.17).
Возможно, однако, что истинное значение 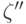 вероятности
появления первого состояния природы принадлежит другому интервалу
вероятности
появления первого состояния природы принадлежит другому интервалу 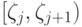 ,
, 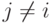 .
Тогда байесовскому критерию относительно этого
распределения соответствует другая критическая
область Q1(j) из (18.17) и,
следовательно, байесовский риск
.
Тогда байесовскому критерию относительно этого
распределения соответствует другая критическая
область Q1(j) из (18.17) и,
следовательно, байесовский риск 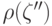 определяется
выражением (18.21) при других
вероятностях ошибок первого и второго рода. Поэтому может случиться, что
ожидаемые потери
определяется
выражением (18.21) при других
вероятностях ошибок первого и второго рода. Поэтому может случиться, что
ожидаемые потери 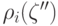 окажутся значительно больше
потерь
окажутся значительно больше
потерь 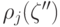 , соответствующих байесовскому риску. Более
того, они могут оказаться выше, чем максимально возможный байесовский риск
, соответствующих байесовскому риску. Более
того, они могут оказаться выше, чем максимально возможный байесовский риск 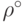 из (18.27). Именно такой случай представлен
на рис. 4.4.
из (18.27). Именно такой случай представлен
на рис. 4.4.
Поэтому в случае неизвестного априорного распределения для состояний
природы, целесообразно использовать минимаксную стратегию, которая
гарантирует уровень ожидаемых потерь, не превышающий значения 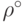 из (18.27).
из (18.27).
В рассматриваемом классе задач такая стратегия может быть построена как
случайная смесь двух чистых стратегий. Эти чистые стратегии задаются
критическими областями Q1(i-1) и Q1(i). При этом
номер i соответствует точке 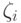 , в которой
достигается максимум функции
, в которой
достигается максимум функции 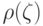 , т.е.
, т.е.  . Указанным
областям Q1(i-1) и Q1(i) соответствуют функции
. Указанным
областям Q1(i-1) и Q1(i) соответствуют функции 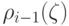 и
и 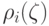 из (18.26), удовлетворяющие условиям
из (18.26), удовлетворяющие условиям
 |
( 19.1) |
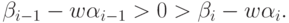 |
( 19.2) |
Пусть критическая область Q1(i-1) используется с
вероятностью  , а область Q1(i) - с вероятностью
, а область Q1(i) - с вероятностью 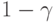
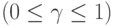 . Тогда
ожидаемые потери статистика определяются взвешенной суммой
. Тогда
ожидаемые потери статистика определяются взвешенной суммой
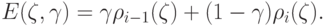 |
( 19.3) |
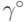 ,
, 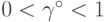 ,
обеспечивающее выполнение равенств
,
обеспечивающее выполнение равенств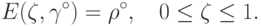 |
( 19.4) |
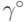 из (19.4), является минимаксной стратегией статистика.
из (19.4), является минимаксной стратегией статистика.Подставим правую часть выражения (18.26)
во взвешенную сумму (19.3). В полученном выражении приравняем
к нулю коэффициент при  и из этого равенства выведем формулу
для значения вероятности
и из этого равенства выведем формулу
для значения вероятности 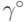 , удовлетворяющего
условию (19.4):
, удовлетворяющего
условию (19.4):
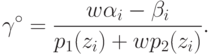 |
( 19.5) |
При этом
![\rho^\circ = w[\alpha_i - \gamma^\circ p_2(z_i)].](/sites/default/files/tex_cache/d613b1aa451a4e66f7e1223fe64a20f5.png) |
( 19.6) |
В качестве иллюстрации укажем, что для функции байесовских потерь,
представленной на рис. 4.4, условие (19.2)
выполняется для значения i=3 и, согласно (19.5)
и (19.6), имеют место оценки  и
и 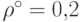 .
Следовательно, минимаксная стратегия для примера,
характеризуемого данными из табл. 4.4,
обеспечивается равновероятным
использованием критических областей Q1(2)={z1,z2},
и Q1(3)= {z1,z2,z3}.
.
Следовательно, минимаксная стратегия для примера,
характеризуемого данными из табл. 4.4,
обеспечивается равновероятным
использованием критических областей Q1(2)={z1,z2},
и Q1(3)= {z1,z2,z3}.
Замечание 4.4. Поскольку 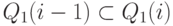 ,
то попадание выборочной точки z в критическую область Q1(i-1) ведет к отвержению
нуль-гипотезы независимо от того, какой из двух критериев будет выбран
рулеткой, соответствующей рассмотренной смешанной стратегии. Принятие
нуль-гипотезы при появлении любого исхода zj,
,
то попадание выборочной точки z в критическую область Q1(i-1) ведет к отвержению
нуль-гипотезы независимо от того, какой из двух критериев будет выбран
рулеткой, соответствующей рассмотренной смешанной стратегии. Принятие
нуль-гипотезы при появлении любого исхода zj, 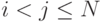 ,
также не зависит от результата случайного выбора
критериев. Случайный выбор оказывается существенным лишь в случае, когда
исходом испытания является значение zi, поскольку
,
также не зависит от результата случайного выбора
критериев. Случайный выбор оказывается существенным лишь в случае, когда
исходом испытания является значение zi, поскольку 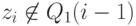 и
и 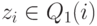 .
.
Поэтому естественно задавать процедуру случайного выбора с помощью набора условных распределений вида
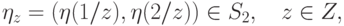 |
( 19.7) |
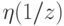 есть вероятность отвержения нуль-гипотезы после наблюдения
выборочной точки
есть вероятность отвержения нуль-гипотезы после наблюдения
выборочной точки  , а
, а 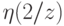 есть вероятность ее принятия при
том же условии. При этом набор (19.7)
условных распределений
есть вероятность ее принятия при
том же условии. При этом набор (19.7)
условных распределений 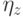 , обеспечивающий
реализацию указанной процедуры, определяется следующими условиями (эти
условия гарантируют тот же уровень ожидаемых потерь, что и рассмотренная
выше минимаксная стратегия ):
, обеспечивающий
реализацию указанной процедуры, определяется следующими условиями (эти
условия гарантируют тот же уровень ожидаемых потерь, что и рассмотренная
выше минимаксная стратегия ):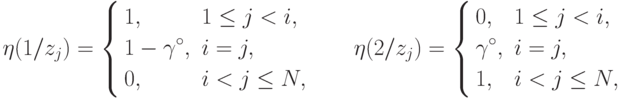 |
( 19.8) |
Как следует из вида распределений (19.8), фактический запуск случайного механизма необходим лишь в тех случаях, когда исход испытания совпадает с единственным значением zi.
Отметим еще одно обстоятельство. Как следует из (17.18)
и (17.20), байесовское решение относительно любого заданного
распределения  достижимо в классе чистых
стратегий
достижимо в классе чистых
стратегий 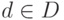 . В случае, когда одна из
функций
. В случае, когда одна из
функций 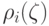 из (18.26) удовлетворяет условию
из (18.26) удовлетворяет условию  и, следовательно1Равенства (19.9) являются следствием вогнутости
функции байесовского риска.,
и, следовательно1Равенства (19.9) являются следствием вогнутости
функции байесовского риска.,
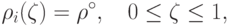 |
( 19.9) |
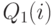 , является чистой минимаксной стратегией
статистика. Однако, в общем случае,
условия (19,9) могут не иметь места. Тогда минимаксная стратегия статистика реализуема
лишь в классе процедур, использующих случайные механизмы
выбора.
, является чистой минимаксной стратегией
статистика. Однако, в общем случае,
условия (19,9) могут не иметь места. Тогда минимаксная стратегия статистика реализуема
лишь в классе процедур, использующих случайные механизмы
выбора.
