|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Устойчивость и эффективность поведения сторон: принцип максимума гарантированного результата
Проблема сравнения стратегий
Вернемся к рассмотрению описанного выше примера и рассмотрим вопрос о
выборе стратегии, которую целесообразно использовать первой стороне для
подготовки к участию в конкурсе. Очевидно, что формирование представления
о лучшей стратегии 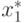 стороны P1 предполагает
либо возможность определения лучшего варианта для любой пары стратегий
стороны P1 предполагает
либо возможность определения лучшего варианта для любой пары стратегий 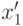 ,
, 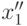 этой стороны, либо возможность
установления равноценности
стратегий, входящих в эту пару. Однако на множестве
стратегий стороны P1 не существует отношения предпочтения,
позволяющего ответить на эти вопросы для любой пары
этой стороны, либо возможность
установления равноценности
стратегий, входящих в эту пару. Однако на множестве
стратегий стороны P1 не существует отношения предпочтения,
позволяющего ответить на эти вопросы для любой пары 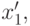
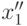 .
.
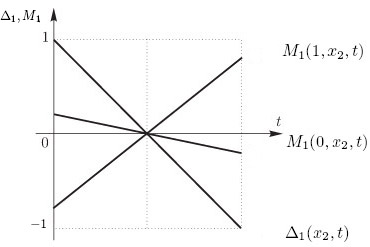
Проиллюстрируем это важное обстоятельство путем сравнения уровней эффективности, обеспечиваемых соответственно стратегиями x1=0 и x1=1. Согласно (1.19) и (1.20),
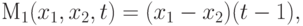 |
( 2.1) |
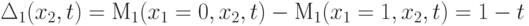 |
( 2.2) |

и, 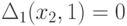 (см. рис. 1.2).
(см. рис. 1.2).
Таким образом, при неизвестном состоянии природы стратегии x1=0 и x1=1 оказываются несравнимыми.
Следовательно, введенная в модели упорядоченность всех исходов операции, с помощью которой мы описали интересы первой стороны, не порождает полного отношения предпочтений на множестве стратегий этой стороны. Причина состоит в том, что неопределенность значения параметра t вызывает неопределенность самого исхода. Поэтому возможность оценки эффективности конкретной стратегии, которая необходима для определения наилучшего выбора, оказывается фундаментально связанной с информированностью стороны о состоянии природы и (в общем случае) о действиях другой стороны.
Принцип максимума гарантированного результата
Как следует из предшествующего рассмотрения, для обеспечения сравнимости стратегий принципиально необходимо принять некоторую гипотезу о неизвестном состоянии природы. В рассматриваемом примере вся имеющаяся у стороны P1 информация о сроке t проведения конкурса сводится к знанию интервала [0, 2], заведомо содержащего этот неизвестный срок. В связи с указанной неопределенностью состояния природы, в качестве оценки эффективности любой стратегии можно принять тот уровень эффективности, который гарантируется использованием этой стратегии.
Замечание 1.7 (об ориентации на худший случай). Фактически, принятие гарантируемого стратегией уровня эффективности в качестве оценки, на которой будет основано сравнение этой стратегии с другими, означает ориентацию на худший случай.
Принятие такой оценки в качестве прогноза результатов планируемых действий является рекомендацией, основанной на обширном опыте принятия решений в практической деятельности. К этому "правилу худшего случая" приходят многочисленные исследователи опыта принятия решений, относящегося к самым различным областям человеческой деятельности. Приведем несколько примеров.
Известный американский специалист в области создания больших программных систем Ф.П. Брукс отмечает, что "наши методы оценки весьма несовершенны. Строго говоря, они отражают некоторое неявно высказываемое и в корне неверное допущение, что все будет идти хорошо, ... выполнение каждого задания займет ровно столько времени, сколько оно "должно" занять". И далее: "Планируйте неудачу: она вас, так или иначе, найдет1Брукс Ф.П. Как проектируются и создаются программные комплексы. М.: Наука, 1978. ".
Можно даже говорить о возникновении своего рода "фольклора", вызванного к жизни необходимостью ориентации на худший случай в практике принятия решений. К числу таких новых жанров относятся, например, так называемые "законы Мэрфи2См., например, Хьюз Дж., Мичтом Дж. Структурный подход к программированию. М.: Мир, 1980. ":
- Все сложнее, чем кажется.
- Все тянется дольше, чем можно ожидать.
- Все оказывается дороже, чем планировалось.
- Если что-то может испортиться, оно обязательно испортится.
По поводу этих законов некто Каллаген сделал следующее замечание3См. там же. "Мэрфи был оптимистом". Действительно, например, второй из "законов" неявно предполагает, что планируемая работа, в конце концов, все-таки завершится. Но этого успешного завершения может и не быть. В книге Дж.Фокса4Фокс Дж. Программное обеспечение и его разработка. М.: Мир, 1985. сообщается, что "военно-воздушные силы США затратили более 300 млн. долларов на тщетную попытку автоматизировать комплексную систему перевозок и снабжения".
Вернемся к рассматриваемому примеру и построим оценку эффективности, которую гарантирует стратегия x1 стороны P1 при неизвестном сроке t проведения конкурса. Эта оценка худшего случая, очевидно, определяется величиной
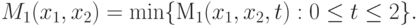 |
( 2.3) |
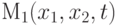 ,
приводим оценку (2.3) к виду
,
приводим оценку (2.3) к виду 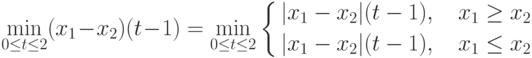 |
( 2.4) |
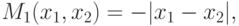 |
( 2.5) |
Первый случай соответствует ситуации, когда 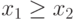 , а
второй - ситуации, когда
, а
второй - ситуации, когда  , т.е.
, т.е.
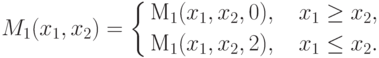 |
( 2.6) |
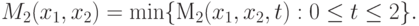 |
( 2.7) |
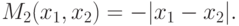 |
( 2.8) |
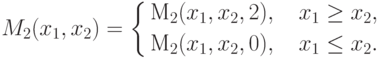 |
( 2.9) |
Таким образом, согласно (2.5) и (2.8),
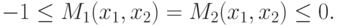 |
( 2.10) |
Следовательно, при ориентации обеих сторон на худший случай (т.е. при использовании ими оценок гарантированного уровня эффективности) противоположность интересов сторон, характеризуемая нулевой суммой критериев (1.21), сменяется ситуацией полного совпадения интересов.