|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Анализ антагонистической игры на основе принципа максимума гарантированного результата
Пример 1.4 (поиск решения антагонистической игры путем вычисления максимального гарантированного результата) Рассмотрим региональный рынок, на котором спрос на некоторый товар носит сезонный характер. Таким товаром может, в частности, быть посевной материал, не допускающий длительного хранения (например, рассада для выращивания овощей в открытом грунте). Будем полагать, что покупателями этого товара являются многочисленные независимые производители соответствующей сельхозпродукции, приобретающие материал непосредственно перед посевными работами и традиционно не имеющие фьючерских1 Фьючерские операции - срочные сделки, представляющие собой куплю-продажу по фиксируемой в момент заключения сделки цене с исполнением операции через определенный промежуток времени. соглашений на поставку материала.
Рассмотрим ситуацию, когда некоторая фирма P1 ставит задачу захвата данного регионального рынка путем проведения единовременной массированной рекламной кампании. Такая кампания может, например, включать демонстрации образцов, встречи с известными экспертами, показы фильмов, публикации в средствах массовой информации, проведение конкурсов и т.п. Стержнем кампании является демонстрация преимуществ предлагаемого материала и технологии ведения работ по сравнению с существующими (при тех же затратах).
Руководство фирмы решает вопрос о том, за какое время x до
начала массовых закупок посевного материала следует запустить указанную
единовременную кампанию. Будем называть соответствующую величину x временем упреждения и
примем масштаб времени, при котором максимальное упреждение не превышает единицы, т.е. ![x \in [0,1]](/sites/default/files/tex_cache/c75c22c0876976bad2957525698cc870.png) .
.
Положим, что фирма P1 имеет значительный опыт продвижения своей продукции на региональные рынки и это позволяет ей оценить вероятность p1(x) успешного захвата рынка в случае проведения рекламной кампании с упреждением, равным времени x. Естественно принять, что эта вероятность (строго) монотонно возрастает, приближаясь к значению p1(0)=1, по мере уменьшения упреждения x (1.14). Т.е. проведение рекламной кампании непосредственно перед периодом массовых закупок (когда вопрос о посевном материале оказывается в фокусе интересов и внимания покупателей) гарантирует захват рынка в силу действительных достоинств новой продукции.
Теперь примем, что этот же региональный рынок пытается захватить другая фирма P2, которая также планирует проведение единовременной рекламной кампании за некоторое время y (из уже рассмотренного интервала [0,1] ) до начала массовых закупок. Фирма P2, как и фирма P1, строит свою кампанию, опираясь на превосходство предлагаемого ею товара над традиционно продаваемым материалом. Опыт фирмы позволяет ей оценить вероятность p2(y) захвата рынка как некоторую (строго) монотонно убывающую функцию времени упреждения y. При этом p2(0)=1. Указанная оценка p2(y) основана на предположении, что конкурирующая фирма P1 не захватила рынок в более ранний момент (т.е. при x>y ), закрепив этот захват заключением договоров на поставку своей продукции. Последнее обстоятельство относится и к оценке p1(x), которая справедлива лишь при условии, что фирма P2 еще не захватила рынок, начав свою кампанию с большим упреждением y>x. Таким образом, с одной стороны, каждая фирма заинтересована задержать начало рекламной кампании, чтобы увеличить вероятность успеха. С другой стороны, существует риск поплатиться за ожидание утратой всякой возможности захватить рынок.
Условимся, что момент принятия решения настолько удален от времени начала закупок, что
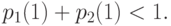 |
( 7.1) |
Перейдем к описанию полезностей, характеризующих исходы операции. Примем, что успешный захват рынка фирмой Pi обеспечивает ей единичную полезность (i=1,2). При этом значение полезности для фирмы, уступившей рынок, полагается отрицательным и равным -1.
Рассмотрим ситуацию, когда рекламные акции обеих сторон проводятся одновременно (т.е. при равных упреждениях x=y ). Возможно (вероятность этого случая равна величине (1-p1(x))(1-p2(y)),x=y), что ни одна из фирм не сможет захватить рынок (или его часть) и он останется за традиционным поставщиком. Такая ситуация полагается более предпочтительной, чем победа конкурента, и мы примем, что ей соответствуют нулевые полезности для обеих сторон.
Возможен (с вероятностью, равной величине p1(x)p2(y), x=y ) случай, когда каждая из сторон сможет захватить некоторый сегмент рынка. При этом обе фирмы могут быть как самостоятельными производителями товара (возможно, разного качества), так и дилерами2Дилер - оптовый покупатель товаров и услуг для розничной перепродажи их потребителям. одного и того же производителя. Они могут также быть производителями, действующими на основе франшизы3Франшиза - право на производство продукции другой компании. от одной и той же компании. В этих случаях их рекламная акция будет сфокусирована на лучших условиях доставки и сопровождения товара (т.е. на качестве соответствующих услуг), что может иметь не одинаковую привлекательность для разных категорий покупателей. Эти и другие обстоятельства могут влиять на характер раздела рынка фирмами P1, P2 и традиционным поставщиком. Описанные случаи также предпочтительнее, чем полная победа конкурента, и мы примем, как и выше, что им соответствуют нулевые полезности для обеих сторон.
Замечание 1.17 (об усреднении полезностей ). Описанная операция, фактически, содержит неконтролируемые сторонами параметры (хотя эти параметры и не указаны явно). Выбор сторонами P1 и P2 решений x и y еще не определяет исхода операции. Прогнозирование этого исхода на основе оценки для худшего случая будет означать отказ от важной информации, которую дают вероятности p1(x) и p2(y) захвата рынка. Возможный способ учета такой информации состоит в том, чтобы оценивать выбираемые решения на основе математических ожиданий полезностей сторон, соответствующих этим решениям. Этот прием использования математических ожиданий для исключения из рассмотрения неконтролируемых состояний природы называется усреднением полезностей
Определим математическое ожидание полезности для стороны P1 как функцию решений x, y и будем рассматривать эту величину как ядро обсуждаемой антагонистической игры. При x>y сторона P1 с вероятностью p1(x) захватывает рынок, обеспечивая себе полезность, равную +1. В случае неудачи, вероятность которой равна 1-p1(x), сторона P2 захватывает рынок, проведя свою рекламную акцию накануне периода закупок. При этом полезность такого исхода для стороны P1 составляет -1. Таким образом,
![M(x,y) = p_1(x) - [1 - p_1(x)] = 2 p_1(x) - 1,\ 0 \le y < x \le 1.](/sites/default/files/tex_cache/c9c377bc05e8c420ce8f7c778b6aa527.png)
Аналогично, при x<y стороны P1 и P2 захватывают рынок с вероятностями, равными соответственно 1-p2(y) и p2(y). Поэтому
![M(x,y) = [1 - p_2(y)] - p_2(y) = 1 - 2p_2(y),\ 0 \le x < y \le 1.](/sites/default/files/tex_cache/1cb76783a6ae3a26f312eae133295862.png)
В случае одновременных рекламных акций (т.е. при x=y ) захват рынка сторонами P1 и P2 имеет место с вероятностями равными, соответственно
![p_1(x)[1 - p_2(x)]\ \text{и } p_2(x)[1 - p_1(x)].](/sites/default/files/tex_cache/ced9d94eae591f7c065e6d9766e19a3f.png)
Следовательно,
![M(x,y) = p_1(x)[1 - p_2(x)] - p_2(x)[1 - p_1(x)] = p_1(x) - p_2(x),\ x = y,](/sites/default/files/tex_cache/a203b0bb2a82f9bd89734111e6cecd5e.png)
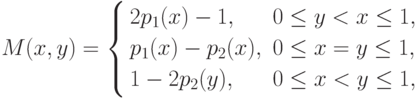 |
( 7.2) |

