|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Смешанные стратегии и проблема устойчивости решений
Защитная роль смешанных стратегий
Как следует из последней рассмотренной теоремы (см. "Приведение позиционной игры к игре в нормальной форме. Условия существования стратегического равновесия" ), наличие у сторон полной информации о развитии игры гарантирует существование стратегических решений, обладающих свойством устойчивости по Нэшу. Вместе с тем, когда такая информация отсутствует, устойчивые решения могут не существовать. Рассмотренная выше игра "погоня за конкурентом" (см. "Нормальная форма конечной игры. Задание конечной игры в позиционной форме" ) является примером именно такого рода, если допустить, что сторона P2, принимает свои решения, не имея информации о первом выборе стороны P1. Рассмотрим еще один подобный пример.
Пример 2.4 (борьба реклам). Фирмы P1 и P2 планируют организовать продажу нового однотипного товара (имеющего, однако, разные фирменные наименования) в супермаркетах двух удаленных друг от друга населенных пунктов П1 и П2. При этом, с целью заблаговременного формирования положительного мнения о своем товаре, который должен потеснить некоторые другие (близкие по характеру использования) товары, фирмы проводят серию рекламных акций, включающих продажу пробных партий в супермаркетах. Фирма P1 располагает большим рекламным опытом и поэтому мнение потребителей о ее товаре окажется выше, чем их мнение о товаре фирмы P2, если рекламные акции обеих сторон будут проходить в одном и том же супермаркете в одно и то же время. Поэтому фирма P1, стремящаяся к монополии на новом рынке, заинтересована проводить свои рекламные акции одновременно и одноместно с фирмой P2. Интересы фирмы P2, трезво оценивающей свои рекламные возможности, являются противоположными.
Каждая акция проводится в одном супермаркете в течение одного торгового дня. При этом ограниченность ресурсов, необходимых для рекламы, не позволяет фирмам проводить свои акции одновременно в обоих пунктах П1 и П2. Таким образом, реализация каждой акции предполагает выбор места (П1 или П2) для ее проведения.
Примем, что для фирмы P1 полезность исхода, соответствующего
одновременной и одноместной рекламной акции обеих фирм, равна +1.
При этом полезность исхода, соответствующего проведению рекламных акций двух фирм
в разных пунктах, фирма P1 оценивает как -1.
Поскольку, как уже отмечалось, интересы фирм являются противоположными, то описанной задаче
выбора места для рекламной акции соответствует антагонистическая игра
с  матрицей из табл. 2.5.
матрицей из табл. 2.5.
| Матрица игры "борьба реклам" | Стратегия P2 | ||
| П1 | П2 | ||
Стратегия P1 в игре 
|
П1 | a11=1 | a12=-1 |
| П2 | a21=-1 | a22=1 | |
Заметим, что коэффициенты этой матрицы совпадают с элементами матрицы из табл. 2.1, соответствующей игре в орлянку, которая рассмотрена 2 "Нормальная форма конечной игры. Задание конечной игры в позиционной форме" . Матрица игры не содержит седловых значений. Сторона P1 может гарантировать себе лишь нижнюю цену игры (т.е. полезность, равную -1 ). Аналогично, сторона P2 может гарантировать, что ее проигрыш не превысит верхней цены игры (т.е. величины, равной +1 ). Напомним, что в антагонистической игре критерии эффективности сторон связаны отношением M1+M2=0 (см. определение в "Математическая модель задачи выбора решений" ).
В условиях рассмотренного примера фирма P1 могла бы увеличить эффективность своей рекламы (по сравнению с гарантированным уровнем полезности, равным -1 ), если бы ей был известен выбор стороны P2. В этом случае, выбрав тот же пункт, что и фирма P2, сторона P1 обеспечивает себе положительную полезность, равную +1. Заметим, что сторона P2 находится в таком же положении. Если ей становится известным, какой именно пункт выбран стороной P1 для проведения рекламной акции, то, выбрав другой пункт, сторона P2 увеличивает свой выигрыш по сравнению с гарантированным уровнем.
Таким образом, в игре без устойчивых стратегических решений получение информации о действиях другой стороны может существенно увеличивать выигрыш. Утечка такой информации может быть как результатом разведывательных действий другой стороны, так и следствием того, что одна из сторон предсказуема в своих действиях, поскольку придерживается заранее принятого графика рекламных акций (т.е. имеет некоторый стереотип поведения, который может быть раскрыт путем наблюдений).
Возможный способ предотвращения утечки информации состоит в том, чтобы отказаться от выбора вариантов в соответствии с принятым (и допускающим раскрытие) планом. Можно предоставить этот выбор случайному механизму (т.е. некоторому случайному процессу, имеющему заданное число исходов с заданными вероятностями их наступления). Реализуем такой подход в рассмотренном примере борьбы реклам.
Пусть сторона P1 выбирает стратегии П1 и П2 соответственно
с вероятностями x и 1-x, где ![x \in
[0{,}1]](/sites/default/files/tex_cache/b46c4581db715b45827831801d95e9b9.png) .
Когда
.
Когда 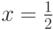 , указанный случайный выбор можно
реализовать, например, путем бросания
симметричной монеты. При этом выбор пункта П1 можно связать с выпадением
"Орла", а выбор пункта П2 - с выпадением "Решки".
Случай
, указанный случайный выбор можно
реализовать, например, путем бросания
симметричной монеты. При этом выбор пункта П1 можно связать с выпадением
"Орла", а выбор пункта П2 - с выпадением "Решки".
Случай 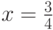 может быть реализован бросанием
симметричной монеты дважды. При этом двум
последовательным реализациям "Решки" сопоставляется выбор
пункта П2, а во всех остальных случаях выбирается пункт П1.
Для произвольных значений x,
может быть реализован бросанием
симметричной монеты дважды. При этом двум
последовательным реализациям "Решки" сопоставляется выбор
пункта П2, а во всех остальных случаях выбирается пункт П1.
Для произвольных значений x, 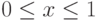 ,
можно использовать компьютерные датчики псевдослучайных
чисел, равномерно распределенных в отрезке [0,1]. При этом
реализация значения
,
можно использовать компьютерные датчики псевдослучайных
чисел, равномерно распределенных в отрезке [0,1]. При этом
реализация значения 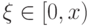 связывается с выбором варианта П1.
В остальных случаях (т.е. при
связывается с выбором варианта П1.
В остальных случаях (т.е. при ![\xi \in [x,1])](/sites/default/files/tex_cache/b6fc69838468bb66a0f8bd6a589947ce.png) выбирается
вариант П2. Все такие случайные механизмы, используемые в задачах выбора вариантов
решения, часто называют рулетками1Термином рулетка
первоначально называлось устройство для азартной игры. В этой игре
участники делают ставки на номер лунки, в которую попадет шарик после
остановки вращающегося круга.
. Применительно к целям нашего
рассмотрения, конкретное устройство рулетки является несущественным. Важно
лишь то распределение вероятностей исходов, которое реализуется выбранным
случайным механизмом.
выбирается
вариант П2. Все такие случайные механизмы, используемые в задачах выбора вариантов
решения, часто называют рулетками1Термином рулетка
первоначально называлось устройство для азартной игры. В этой игре
участники делают ставки на номер лунки, в которую попадет шарик после
остановки вращающегося круга.
. Применительно к целям нашего
рассмотрения, конкретное устройство рулетки является несущественным. Важно
лишь то распределение вероятностей исходов, которое реализуется выбранным
случайным механизмом.
Поскольку в рамках нового подхода выбор стороны P1 является случайным, сторона P2 не может предсказать его исход. Эта неопределенность является результатом искусственного введения в задачу некоторого неуправляемого параметра. При этом стороны могут ориентироваться лишь на математическое ожидание полезности
 |
( 10.1) |
Введя случайный механизм выбора, мы фактически расширили исходную модель.
В этом расширении игрок P2 по-прежнему выбирает стратегию
с некоторым номером j (j=1,2). Но выбор стратегии i (i=1,2) первого игрока осуществляется случайным механизмом.
Игрок P1, задавая число x 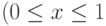 ), выбирает лишь распределение
вероятностей для этого случайного механизма, но не конкретную
стратегию i. Это распределение называют смешанной стратегией первого игрока, поскольку
ее реализация во многих партиях игры порождает некоторую "смесь"
стратегий i=1 и i=2.
), выбирает лишь распределение
вероятностей для этого случайного механизма, но не конкретную
стратегию i. Это распределение называют смешанной стратегией первого игрока, поскольку
ее реализация во многих партиях игры порождает некоторую "смесь"
стратегий i=1 и i=2.
Поскольку при x=1 случайный механизм рождает (с единичной вероятностью) выбор i=1, а при x=0 - выбор i=2, то прежние стратегии реализуются и при игре в смешанных стратегиях. Для различения смешанных стратегий игрока P1 и стратегий i=1 и i=2, которые он использовал в исходной игре, последние обычно называют чистыми стратегиями.
Проведем анализ ядра (10.1),
соответствующего расширению исходной игры путем введения
смешанных стратегий первого игрока. Выбирая конкретное значение ![x\in [0,1]](/sites/default/files/tex_cache/c628ba2b1047de93f66cb815d986e107.png) , игрок P1 гарантирует себе следующее
значение математического ожидания полезности исхода:
, игрок P1 гарантирует себе следующее
значение математического ожидания полезности исхода:
 |
( 10.2) |
Графики на рис. 2.7 представляют отрезки прямых линий 2x-1 и 1-2x, причем нижняя огибающая этого семейства, соответствующая правой части равенства (10.2), выделена жирными линиями. Как следует из этого рисунка, при любом значении x, не совпадающем с нулем или единицей, справедливо неравенство:

Т.е. любая смесь стратегий гарантирует стороне P1 математическое ожидание полезности, превосходящее нижнюю цену игры.
При этом выбор значения  позволяет повысить этот гарантированный уровень до нулевого значения:
позволяет повысить этот гарантированный уровень до нулевого значения:

Пусть теперь второй игрок также выбирает свою чистую стратегию с помощью
рулетки, задаваемой распределением вероятностей (y,1-y),
где 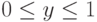 . Математическое ожидание выигрыша первого игрока
(т.е. ядро игры) в этом (полном) смешанном расширении
исходной игры определяется выражением:
. Математическое ожидание выигрыша первого игрока
(т.е. ядро игры) в этом (полном) смешанном расширении
исходной игры определяется выражением:
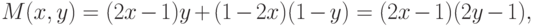
![(\forall x,y \in [0,1]) M(x, \frac{1}{2}) \le M(\frac{1}{2},
\frac{1}{2}) \le M(\frac{1}{2}, y),](/sites/default/files/tex_cache/4454d09484e718cd6accc729d8cf8672.png) |
( 10.3) |
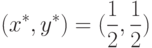
Таким образом, смешанное расширение рассмотренной игры, не имевшей устойчивых решений в чистых стратегиях, имеет устойчивое (и эффективное) решение в смешанных стратегиях. Как будет показано в следующем параграфе, этот вывод носит общий характер (т.е. он не связан с конкретными значениями элементов матрицы из рассмотренного примера). Указанный вывод в сочетании с доказанной выше теоремой (см. "Приведение позиционной игры к игре в нормальной форме. Условия существования стратегического равновесия" ) можно интерпретировать следующим образом. Достаточным условием существования устойчивых (по Нэшу) решений матричной игры является равная информационная обеспеченность игроков. Либо обе стороны располагают информацией обо всех сделанных выборах (что соответствует игре с полной информацией), либо обе стороны не могут достоверно прогнозировать решения друг друга (что обеспечивается использованием смешанных стратегий). Как мы увидим ниже, этот вывод справедлив и для биматричных игр.
Замечание 2.4. Поскольку, согласно (10.3)
![(\forall x, y \in [0,1]) M(x^\ast, y) = M(x, y^\ast) = v = 0,](/sites/default/files/tex_cache/26eee443eb2b799765005c1953175bbc.png)