Потоки в сетях
Приложение
Теорема о максимальном потоке и минимальном разрезе позволяет проверять, максимален данный поток или нет, но только для достаточно простых сетей. Разумеется, на практике приходится иметь дело с большими и сложными сетями, и в общем случае трудно найти максимальный поток простым подбором. Опишем один алгоритм нахождения максимального потока в любой сети с целочисленными пропускными способностями. Перенесение этого алгоритма на сети с рациональными пропускными способностями осуществляется тривиальным образом и предоставляется читателю.
Шаг 1. Сначала подберем
поток  , обладающий ненулевой
величиной (если такой поток существует). Стоит отметить, что чем больше
величина выбранного нами начального потока
, обладающий ненулевой
величиной (если такой поток существует). Стоит отметить, что чем больше
величина выбранного нами начального потока  , тем проще
будут последующие шаги.
, тем проще
будут последующие шаги.
Шаг 2. Исходя из  , строим новую сеть
, строим новую сеть  путем изменения
направления потока
путем изменения
направления потока  на противоположное. Более точно, любая
дуга
на противоположное. Более точно, любая
дуга  , для которой
, для которой  , остается
в
, остается
в  со своей первоначальной пропускной способностью, а любая дуга
со своей первоначальной пропускной способностью, а любая дуга  , для
которой
, для
которой 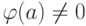 , заменяется дугой
, заменяется дугой  с пропускной
способностью
с пропускной
способностью  и противоположно направленной
дугой с пропускной способностью
и противоположно направленной
дугой с пропускной способностью 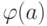 .
.
Шаг 3. Если в сети  мы сможем найти ненулевой поток из
мы сможем найти ненулевой поток из  в
в  , то его можно добавить к первоначальному потоку
, то его можно добавить к первоначальному потоку  и получить в
и получить в  новый поток
новый поток  большей
величины. Теперь можно повторить шаг 2, используя при построении сети
большей
величины. Теперь можно повторить шаг 2, используя при построении сети  новый поток
новый поток  вместо
вместо  . Повторяя эту процедуру,
мы в конце концов придем к сети
. Повторяя эту процедуру,
мы в конце концов придем к сети  , не содержащей ненулевых потоков; тогда
соответствующий поток
, не содержащей ненулевых потоков; тогда
соответствующий поток  будет максимальным потоком.
будет максимальным потоком.
