Теория трансверсалей
Приложение теории трансверсалей
Используются понятия трансверсалей, на основании чего доказывается теорема
о модификации латинского прямоугольника. Вводятся определения 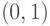 -матрицы, формулируются и доказываются теоремы
Кенига-Эгервари и
об общей трансверсали.
-матрицы, формулируются и доказываются теоремы
Кенига-Эгервари и
об общей трансверсали.
Теорема
Пусть  латинский
латинский  -прямоугольник,
причем,
-прямоугольник,
причем,  ; тогда
; тогда  можно расширить до латинского квадрата добавлением
можно расширить до латинского квадрата добавлением  новых строк.
новых строк.
Доказательство
Докажем, что  можно расширить до латинского
можно расширить до латинского 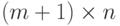 -прямоугольника; повторяя эту процедуру, мы придем к латинскому
квадрату.
-прямоугольника; повторяя эту процедуру, мы придем к латинскому
квадрату.
Пусть 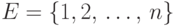 и
и 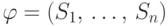 , где через
, где через  обозначено множество, состоящее из тех элементов
множества
обозначено множество, состоящее из тех элементов
множества  , которые не встречаются в
, которые не встречаются в  -м столбце матрицы
-м столбце матрицы  .
Если мы сможем доказать, что
.
Если мы сможем доказать, что  имеет трансверсаль, то тем
самым мы докажем теорему, поскольку элементы этой трансверсали и образуют
дополнительную строку. По теореме Холла достаточно доказать, что
объединение любых
имеет трансверсаль, то тем
самым мы докажем теорему, поскольку элементы этой трансверсали и образуют
дополнительную строку. По теореме Холла достаточно доказать, что
объединение любых  множеств
множеств  содержит по
меньшей мере
содержит по
меньшей мере  различных элементов. А это очевидно, ибо любое такое объединение содержит
различных элементов. А это очевидно, ибо любое такое объединение содержит 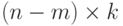 элементов (включая повторения), значит, по крайней
мере, один из них повторялся бы более чем
элементов (включая повторения), значит, по крайней
мере, один из них повторялся бы более чем  раз, что
невозможно.
раз, что
невозможно.
Определение (0,1) матрицы или матрицы инциденций.
Другой подход к изучению трансверсалей семейства 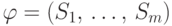 непустых подмножеств множества
непустых подмножеств множества 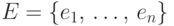 состоит в исследовании
состоит в исследовании 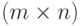 -матрицы
-матрицы 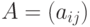 , в
которой
, в
которой 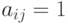 , если
, если  ,
и
,
и 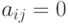 в противном случае. (Любую такую матрицу, все элементы которой
равны
в противном случае. (Любую такую матрицу, все элементы которой
равны  или
или  , мы называем
, мы называем 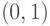 -матрицей) этого семейства.
-матрицей) этого семейства.
Определение словарного
ранга. Назовем словарным
рангом матрицы  наибольшее число единиц
в
наибольшее число единиц
в  , никакие две из
которых не лежат в одной и той же строке или в одном и том же столбце.
Тогда
, никакие две из
которых не лежат в одной и той же строке или в одном и том же столбце.
Тогда  имеет трансверсаль в том и только в том случае, если
словарный ранг матрицы
имеет трансверсаль в том и только в том случае, если
словарный ранг матрицы  равен
равен  . Более того,
словарный ранг матрицы
. Более того,
словарный ранг матрицы  равен в точности числу элементов
частичной трансверсали, обладающей
наибольшей возможной мощностью. В качестве второго приложения теоремы
Холла рассмотрим известный результат о
равен в точности числу элементов
частичной трансверсали, обладающей
наибольшей возможной мощностью. В качестве второго приложения теоремы
Холла рассмотрим известный результат о 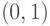 -матрицах, называемой
теоремой Кенига-Эгервари.
-матрицах, называемой
теоремой Кенига-Эгервари.
Теорема (Кенига-Эгервари, 1931)
Словарный ранг 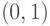 -матрицы
-матрицы  равен минимальному
числу
равен минимальному
числу  строк и
столбцов, которые в совокупности содержат все единицы из
строк и
столбцов, которые в совокупности содержат все единицы из  .
.
Замечание В качестве иллюстрации этой теоремы рассмотрим матрицу
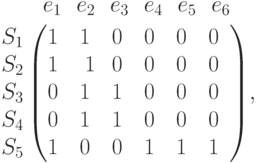
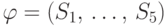 .
Ясно, что и ее словарный ранг, и число
.
Ясно, что и ее словарный ранг, и число  равны четырем.
равны четырем.