Каркасы и изоморфизм деревьев
Изоморфизм деревьев
Два графа  и
и  изоморфны (записывается
изоморфны (записывается  или
иногда
или
иногда 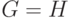 ), если между множествами вершин существует взаимно
однозначное соответствие, сохраняющее смежность.
), если между множествами вершин существует взаимно
однозначное соответствие, сохраняющее смежность.
Инвариант графа  — это
число, связанное с
— это
число, связанное с  , которое
принимает одно и то же значение на любом графе, изоморфном
, которое
принимает одно и то же значение на любом графе, изоморфном  .
Полный набор инвариантов определяет граф с точностью до изоморфизма.
.
Полный набор инвариантов определяет граф с точностью до изоморфизма.
Пусть дерево 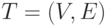 и его
и его 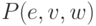 инцидентор, т.е.
предикат, равный единице в том и только в том случае, когда ребро
инцидентор, т.е.
предикат, равный единице в том и только в том случае, когда ребро  инцидентно вершинам
инцидентно вершинам  и
и  .
.
Дерево  называется изоморфным дереву
называется изоморфным дереву  ), если между вершинами деревьев, а также между их
ребрами можно установить взаимно однозначное соответствие
), если между вершинами деревьев, а также между их
ребрами можно установить взаимно однозначное соответствие  и
и  , сохраняющее инцидентор,
т.е. такое, что
, сохраняющее инцидентор,
т.е. такое, что 
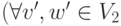

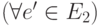 (
( 
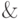

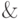
![e \Leftrightarrow e' \Rightarrow [P_1(e,v,w)] =
P_2(e',v',w')](/sites/default/files/tex_cache/d024f4ce51dcb197f580c598656449ba.png) ).
).
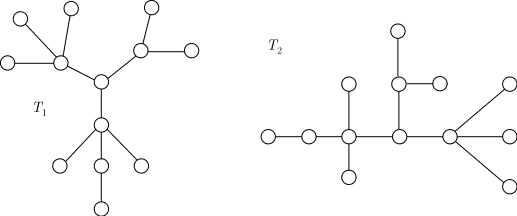
Другими словами, два дерева изоморфны, если между их вершинами можно установить взаимно однозначное соответствие, сохраняющее отношение инцидентности (смежности).
Отношение изоморфизма деревьев рефлексивно, симметрично, транзитивно, т.е. представляет собой эквивалентность. Матрицы смежности изоморфных деревьев могут быть переведены одна в другую перестановкой рядов, т.е. одновременной одинаковой перестановкой строк и столбцов.
Пример изоморфных деревьев: нетрудно заметить, что они отличаются лишь способом представления (например, способом изображения на плоскости).
Два корневых дерева называются изоморфными, если существует взаимно однозначная функция, которая отображает множество вершин одного дерева на множество другого и не только сохраняет смежность, но и переводит корень одного дерева в корень другого.
Изоморфное отображение дерева  на себя называется автоморфизмом
дерева. Совокупность всех автоморфизмов дерева
на себя называется автоморфизмом
дерева. Совокупность всех автоморфизмов дерева  ,
обозначаемая
,
обозначаемая  , образует группу, называемую группой дерева
, образует группу, называемую группой дерева  . Таким
образом, элементы группы
. Таким
образом, элементы группы  являются подстановками,
действующими на множестве вершин
являются подстановками,
действующими на множестве вершин  . Порядок
. Порядок 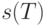 группы
группы  есть число симметрий дерева
есть число симметрий дерева  .
.
Дерево  называется асимметричным, если его группа
автоморфизмов есть единичная группа, т.е.
называется асимметричным, если его группа
автоморфизмов есть единичная группа, т.е. 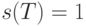 .
.
Примеры асимметричных деревьев порядка 7, 8, 9.
Два плоских дерева называются изоморфными, если существует гомеоморфное отображение плоскости на себя, сохраняющее ориентацию, и такое, что отображает одно из этих деревьев в другое.
Два помеченных дерева называются изоморфными, если существует взаимно однозначная функция, отображающая множество вершин одного дерева на множество вершин другого, которая не только сохраняет смежность, но и переводит вершину с меткой в вершину с той же меткой.