Основы трехмерного "живого" моделирования

Сферическое экранное пространство

Даже при бытовом применении объемного экрана возникает желание кругового обзора с одинаковым качеством изображения. Необходимо рассмотреть возможность экранизации в сферической системе координат . В ней каждая точка характеризуется расстоянием r и двумя углами: азимутом и углом места . Пересчет из декартовой системы производится по формулам , , .

Применение сферической системы координат определяет форму объемного экрана: он становится полусферой (рис.12.7). Центр системы координат совпадает с центром основания прямоугольника.

Однако важным отличием является то, что сами экранные пленки должны быть сферическими. Вместо нарезки на 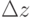, становится актуальной нарезка на 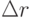. Центр полусферы также выродится в сферическую пленку "на одну точку".

Рис. 12.7. Сферический экран

В компьютерной модели трехмерной памяти весь обозримый объем представляет собой прямоугольник, а, скорее всего, – куб. При преобразовании в сферическую систему координат возникает вопрос: вписать этот куб в полусферу или вписать полусферу в куб? В первом случае нет потери информации, что важно, например, при отображении сценических действий. Однако при этом не используется существенная часть экранного пространства. Во втором случае теряется информация, но увеличивается масштаб представляемого объекта при его центральном размещении. Это важно при построении реагирующих объектов для интеллектуальных систем отображения работы предприятий.

Заметим, что в первом случае "лишнюю" часть сферического экрана можно просто срезать. Получится экран – куб, со сферическим расположением экранных пленок, использующий сферическую систему координат . Торцевой эффект, если такой существует, будет значительно снижен.

увеличить изображение
Рис. 12.8. "Внешнее" экранное пространство

При круговом обзоре экранного пространства важно не допустить, чтобы свечение внешней поверхности экранной пленки было видно с другой ее стороны. Это испортило бы общее впечатление. По-видимому, следует затенять с другой стороны каждую светящуюся точку. Это может потребовать перемежения экранных и затеняющих пленок или нанесения двух слоев "прозрачной электроники" на каждую экранную пленку. И то и другое, несомненно, будет отрицательно влиять на прозрачность и разрешающую способность сферического объемного экрана.

Теоретически возможно выполнение модели трехмерной компьютерной памяти в сферической системе координат . Однако "математика" анимации представляется весьма сложной. Вряд ли это следует считать целесообразным. Ведь со временем экранные пространства, вбирающие лавинные достижения нано-технологий, будут дешеветь. Да и в массовом применении вряд ли привычная сцена превратится в полусферу.

Применение сферических экранных пленок позволяет не только создавать экранные пространства для внешнего наблюдения, но и для "внутреннего" расположения зрителей, для которых этот экран становится "внешним", как показано на рис.12.8. Можно легко себе представить разнообразные применения такого экрана в области туризма и развлечений.

В заключение отметим, что приведенные рассуждения напоминают фантастический сюжет. Однако даже наивная фантастика всегда предшествовала серьезным разработкам. Фантастика ставит задачи. Их реальность основана на текущем уровне знаний. Технология прозрачных мониторов и гибких прозрачных электронных схем подсказывает реализуемый, в сегодняшнем представлении, путь создания средств объемного отображения. Предстоят еще значительные усилия по достижению достаточной прозрачности пакета экранных пленок, и объекты могут казаться, словно выплывающими из мрака. Не следует забывать о создании особой оптической среды со специфическими свойствами и т.д.

Так что вполне возможно, что объемный экран на основе пакета экранных пленок может оказаться временным достижением. Временным, - до нахождения той среды, по координатам точек которой будут доставляться кванты энергии, несущие пиксели свечения.

Ключевые термины

"Живое" моделирование – воссоздание объектов, адекватно реагирующих на внешнее воздействие.

Реагирующие объекты – объекты наглядного отображения ситуации, складывающейся в сложной управляющей, производственной, игровой и др. системе, способные своим поведением предупредить об угрозе или отклонении производственного процесса от нормы и произвести первичную диагностику.

Трехмерная память – память компьютера, адресуемая тремя координатами. Позволяет имитировать графически расположение моделируемого объекта в пространстве.

"Мышцы" и "кости" - реализуют механизм воздействия и управления, посредством преобразования координат точек объекта, при имитации деформаций и движения в трехмерном пространстве.

Прозрачный монитор – выполняется на основе "прозрачного" экрана с размещенными на нем электронными схемами для отображения видимой части объектов. Эти схемы выполняются на основе нано-технологий так, что вне зоны видимого изображения экран остается прозрачным.

Экранный пакет – формируется на базе наложения друг на друга прозрачных экранных пленок, каждая из которых отображает видимый срез демонстрируемого объекта в трехмерной памяти. В результате этого в толще пакета создается стереоэффект.

Сферическая система координат – отражает координаты нахождения точки по расстоянию от центра и по двум углам – азимут и угол места.

Краткие итоги

1. Большое количество показателей современных управляющих и производственных систем затрудняет оперативный мониторинг, проводимый операторами-диспетчерами. Для снижения отрицательной роли человеческого фактора требуется создание автоматического посредника, осуществляющего своевременную реакцию на результаты контроля текущего состояния системы. Такая реакция может учитывать первичную диагностику.
2. Компьютерные технологии мониторинга требуют воплощения реагирующих объектов на базе графического "живого" моделирования.
3. Объемное воплощение и отображение требуют преобразования линейной адресуемой памяти компьютера в трехмерное отображение.
4. Для объектов, размещенных в трехмерной памяти, формируются "мышечные" и "костные" процедуры деформации и движения. Выполнение этих процедур сопрягается с органами управления вне моделируемого объекта.
5. Управление трехмерным объектом осуществляется с помощью логической нейронной сети. Она воспринимает "ситуацию" и преобразует ее в приказы по параметризованному запуску процедур движения для адекватной реакции объекта.
6. На основе применения сферических пакетов экранных пленок возможно создание объемных экранов как для внешнего, так и для внутреннего расположения зрителя.

Вопросы:

1. Что понимается под термином "жизнь" в информационно-техническом аспекте?
2. Как строится модель адресуемой трехмерной памяти?
3. Каковы принципы построения трехмерной графики в модели трехмерной памяти?
4. Как, на принципиальном уровне, формируются процедуры перемещения точек в трехмерной памяти, имитирующие деформации, движения и повороты?
5. Как логическая нейронная сеть осуществляет реагирование на текущие значения параметров сложной системы? Возможна ли при этом первичная диагностика?
6. Как осуществляется трехмерная экранизация "живых" моделей на основе достижений "прозрачной" электроники?

Дополнительные материалы к лекции, Вы можете скачать здесь.