|
"Тогда как задать возбуждение рецепторов, если инспектор точно установил, что скорость автомобиля при наезде на пешехода была равна 114 км/час? Вопрос по расчёту скорости и сумме достоверности: этот математический (приведенный выше в виде контекста из материала лекции 1, страницы 3) метод справедлив к скоростным показателям выходящим за рамки диапазона 100-120. |
Обучение логической нейронной сети
Матрица следования
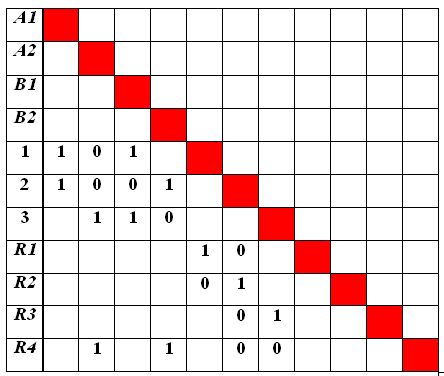
В представленном виде нейронная сеть не годится для формальных исследований, тем более, - на компьютере. Поэтому используются матрицы следования , отображающие как взаимодействие нейронов, так и веса синапсических связей.
Для данного случая матрица следования показана на рис.4.4.
Здесь непустые элементы означают наличие связей, а указанные в них значения соответствуют первоначально заданным нулевым весам этих связей.
В результате выполнения алгоритма обучения логической нейронной сети методом трассировки формируются единичные веса некоторых связей так, чтобы сигналы, характеризующие каждую ситуацию, в наибольшей степени возбуждали поставленные им в соответствие нейроны выходного слоя. Если первоначально заданных связей не хватает, то допускается введение дополнительных связей с единичными весами.
Окончательный результат обучения нейронной сети методом трассировки показан на рис.4.5, где выделены связи с единичными весами. (Другие "проводочки" мы могли бы перекусить.) Так как первоначальных связей оказалось недостаточно, пришлось ввести дополнительные "проводочки" с единичными весами (с нулевым сопротивлением). Матрица следования для обученной нейронной сети представлена на рис.4.6.
Но радоваться рано. Посчитаем с помощью нашей функции активации величины возбуждения нейронов для, например, ситуации A1&B2: 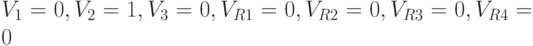 . Ни один нейрон выходного слоя не возбудился! То же — для ситуаций A1&B1 и A2&B1. Рассчитаем ситуацию A2&B2:
. Ни один нейрон выходного слоя не возбудился! То же — для ситуаций A1&B1 и A2&B1. Рассчитаем ситуацию A2&B2:  . Мы видим, что построенная нейросеть распознает единственную ситуацию, заданную четко.
. Мы видим, что построенная нейросеть распознает единственную ситуацию, заданную четко.
Анализируя, мы убеждаемся, что в процессе распространения по сети возбуждение "гаснет", не доходя до выходного слоя. Тогда мы начинаем "подкручивать" пороги, уменьшая их. Но тотчас замечаем другую неприятность: величины возбуждения нейронов выходного слоя различны для разных ситуаций, ибо различна длина путей возбуждения. Это является следствием не аддитивности функции активации, что затрудняет правильное участие нейронов в следующих логических слоях, когда данный выходной слой является входным для следующего логического уровня сети. Мы видим, что наша функция активации не годится для выбранной структуры нейросети.
В предыдущем разделе, посвященном распознаванию символов, была использована "хорошая" функция активации, определяющая величину Vi возбуждения нейрона:

Рассчитайте и убедитесь, что, например, для 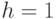 сеть правильно распознает все эталонные ситуации, обеспечивая равную величину возбуждения нейронов выходного слоя. Так, при ситуации A1&B1 получаем следующие величины возбуждения нейронов:
сеть правильно распознает все эталонные ситуации, обеспечивая равную величину возбуждения нейронов выходного слоя. Так, при ситуации A1&B1 получаем следующие величины возбуждения нейронов:  . Аналогично, — для ситуаций A1&B2 и A2&B1. Для ситуации A2&B2 находим
. Аналогично, — для ситуаций A1&B2 и A2&B1. Для ситуации A2&B2 находим  .
.
Сеть работает прекрасно, гарантируя правильность реакции на недостоверные ситуации, и позволяя находить среднее.
А главное, сколько прекрасных вариантов развития имеет игра, стимулируя наше предвидение! Например, что, если скорость паровозов — величина переменная и случайная, так же как и чередование и длина однопутных участков, и решение следует принимать и корректировать в динамике, в зависимости от длины пройденного пути и значения скорости? Что, если один машинист охвачен идеей суицида, а другой желает уклониться от столкновения? и т.д., и т.д. (Бедные линейные!)
Обучение нейросети для "современной" системы принятия решений
Продвинемся еще на шаг по пути иллюстративного освоения принципов обучения логической нейронной сети.
Выберем нейросеть, отражающую, как нам кажется, все особенности, которые необходимо учесть при построении алгоритма трассировки, и, как мы уже начали, возьмем пример из 2.3, который в терминах обобщенных эталонов выглядит теперь следующим образом:
A1&B1&C1&C2&C3&C4&C5  R1
R1
A1&B2&B3&C1&C2&C3  R2
R2
A1&B2&B3&C4&C5  R3 (4.1)
R3 (4.1)
A2&B3&C1&C2&C3&C4&C5  R4
R4
A2&B1&B2&C1&C2&C3&C4&C5  R5
R5
Мы хотим, задавая обобщенный эталон на входе, например, из тех, что приведены выше, экономным путем построить, возможно, пересекающиеся пути возбуждения, ведущие от каждого возбужденного входного нейрона в соответствующий нейрон выходного слоя. Способ должен быть экономным в том смысле, что пути должны быть максимально объединены, совмещены, реализуя стратегию слияния и выхода на общую, единую дорогу, ведущую к заветной цели.
При этом мы используем приведенный в [6, 7] эвристический алгоритм, который крайне экономно расходует ресурсы сети — ее нейроны и связи, но и так же экономно вводит изменения, развивает сеть, если связей оказывается недостаточно.
Ибо мы видели, с каким трудом удается приспособить "готовую" нейросеть под конкретную задачу. Мы постоянно склонялись к вопросу: "А не лучше ли сразу строить сеть "под задачу", а не наоборот?" Нам кажется, мы нашли диалектический компромисс: беря что-то близкое, подходящее, мы минимально переделываем, словно костюм с жмущим гульфиком, купленный в универсальном магазине. Кроме того, нам очень важно сделать алгоритм доступным широким массам студенческой молодежи, овладевшей основами таинства параллельного программирования!
Пусть выбранная нейросеть представлена на рис.4.7, где первоначально заданные связи обозначены тонкими стрелками. Строим соответствующую матрицу следования S и в ней — транзитивные связи (рис.4.8), определяющие транзитные пути попадания в каждый нейрон. Проверяем, все ли нейроны выходного слоя достижимы из любого нейрона входного слоя. Если нет, считаем, что сеть составлена не корректно.
В данном случае из нейрона В1 не исходит ни одного пути, заканчивающегося нейроном Вых5. Это следует из того, что в строке, соответствующей нейрону Вых5, нет даже транзитивной связи в столбце, соответствующем нейрону В1. То же касается нейрона В3.
Введем синапсические связи В1  Вых5 и В3
Вых5 и В3  Вых5 что и отмечено на рис.4.6 жирными стрелками, а на рис.4.7 – нулевыми весами введенных связей.
Вых5 что и отмечено на рис.4.6 жирными стрелками, а на рис.4.7 – нулевыми весами введенных связей.
По первому выражению в (4.1) сформируем статический путь возбуждения {B1, A1, C1, C2, C3, C4, C5}  Вых1, объединяющий только интересующие нас сейчас нейроны и учитывающий только те связи, что могут быть основой необходимой трассы, и отобразим его матрицей
Вых1, объединяющий только интересующие нас сейчас нейроны и учитывающий только те связи, что могут быть основой необходимой трассы, и отобразим его матрицей  [B1,A1,C1,C2,C3,C4,C5
[B1,A1,C1,C2,C3,C4,C5  Вых1] на рис.4.9. Эта матрица формируется на основе матрицы S вычеркиванием всех строк и столбцов, которые соответствуют не интересующим нас нейронам.
Вых1] на рис.4.9. Эта матрица формируется на основе матрицы S вычеркиванием всех строк и столбцов, которые соответствуют не интересующим нас нейронам.
Пытаясь сымитировать прокладываемые пути возбуждений, снабдим все нейроны входного слоя, отраженные в этой матрице, признаком "возбужден".
Найдем входы матрицы  (пустые строки), обладающие признаком "возбужден". Выделим в одну совокупность соответствующие им столбцы, в данном случае столбцы 1 - 7, и найдем в ней строку, содержащую максимальное число "нулей", — строку, соответствующую нейрону 6. Заменяем в этой строке (в выделенной совокупности столбцов) "нули" "единицами", т.е. максимально увеличиваем соответствующие веса. Присваиваем нейрону 6 признак "возбужден", а также значение
(пустые строки), обладающие признаком "возбужден". Выделим в одну совокупность соответствующие им столбцы, в данном случае столбцы 1 - 7, и найдем в ней строку, содержащую максимальное число "нулей", — строку, соответствующую нейрону 6. Заменяем в этой строке (в выделенной совокупности столбцов) "нули" "единицами", т.е. максимально увеличиваем соответствующие веса. Присваиваем нейрону 6 признак "возбужден", а также значение  = 5, характеризующее то количество нейронов, "возбуждение" которых мы "собрали" на входе этого нейрона. Впредь мы можем только повторно использовать этот нейрон, но менять веса связей на его входе мы не должны. Изменение весов отображаем в матрице S.
= 5, характеризующее то количество нейронов, "возбуждение" которых мы "собрали" на входе этого нейрона. Впредь мы можем только повторно использовать этот нейрон, но менять веса связей на его входе мы не должны. Изменение весов отображаем в матрице S.
Исключаем из матрицы  строки и столбцы, соответствующие нейронам С1, С2, С3, С4, С5. Новый вид матрицы
строки и столбцы, соответствующие нейронам С1, С2, С3, С4, С5. Новый вид матрицы  представлен на рис.4.10.
представлен на рис.4.10.