Модель нейронной сети

Формирование информации на рецепторном слое

Определим возбуждение рецепторного слоя, учитывая то, что по нейросетевым технологиям решаются сложные, чаще всего трудно формализуемые задачи. Исходная информация этих задач может быть настолько несовместима по смыслу, типам данных и единицам измерения, что приведение ее к некоторому количественному воплощению — величине возбуждения нейронов входного слоя — представляет серьезную проблему.

Например, как объединить величину превышаемой водителем скорости и тип автомобиля иностранного производства со вчерашним неудачным выступлением любимой автоинспектором футбольной команды, — при нахождении величины штрафа? Ведь каждый из перечисленных факторов должен определить некоторые общие, приведенные значения возбуждения.

Такое приведение также зависит от задачи. Поскольку нейроны — нечто стандартное для данной задачи или класса задач, то каждая характеристика нейрона — величина возбуждения, веса его синапсических связей, порог, функция активации — должны быть одинаковы или принадлежать общему (по каждой характеристике) для всех нейронов диапазону возможных значений.

Дадим рекомендации, основанные на "событийном" принципе.

Разобьем скорость на диапазоны штрафования, например, [90, 100], [100, 110], [110, 120], [120, 200]. За каждым диапазоном скорости закрепим нейрон входного слоя — рецептор.

Универсальный подход основан на связывании величины возбуждения рецептора с достоверностью – вероятностью того, что величина скорости принадлежит одному или нескольким диапазонам. Такому подходу будем следовать в дальнейшем.

А именно, хотя бы интуитивно (а интуиция основана на изучении Инструкции) определим достоверность того, что интересующая нас величина принадлежит данному диапазону. С какой достоверностью она принадлежит второму диапазону? А третьему?

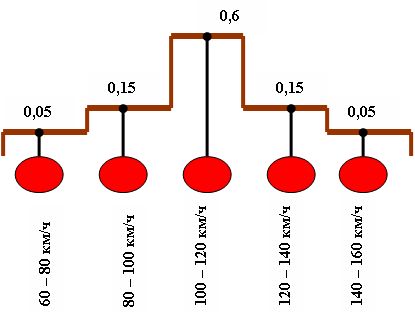
Грамотный инспектор помнит, что должен исходить из свойств ИМС - исчерпывающих множеств событий, с которыми имеет дело. Для ИМС сумма вероятностей событий равна единице. Тогда, в соответствии с высказанными положениями, инспектор не должен, например, задавать значение достоверности того, что скорость автомобиля находится в пределах 100 – 120 км/ч, равной 0,8, и в то же время достоверность того, что она находится в пределах 120 – 140 км/ч, равной 0,7. Более того, в соответствии с рекомендациями теории нечетких множеств он следует нормальному закону распределения плотности вероятностей. А именно, если он считает, что, скорее всего, скорость принадлежит диапазону 100 – 120 км/ч, и полагает достоверность этого высказывания равной 0,6 (математическое ожидание), то куда деть остальные 0,4? Инспектор распределяет эту величину между "смежными" по смыслу событиями, имитируя нормальный закон, например, полагая значения возбуждения рецепторов, как показано на рис.1.11.

Рис. 1.11. Распределение возбуждения рецепторов по нормальному закону

В случае не столь высокой грамотности, полагаясь на универсальность аппарата логических нейронных сетей, имитирующего массовое ассоциативное мышление, можно даже уйти от понятия достоверности, как вероятностной категории. Все ли мы на бытовом уровне знакомы с понятием исчерпывающего множества событий, связанным с условием нормировки, т.е. – с условием равенства единице суммы их вероятностей? Ведь часто можно услышать: "Даю голову на отсечение, что это так, хотя и допускаю, что все наоборот…" Главное, чтобы исходные оценки информации были относительными, отражающими принцип "больше – меньше". Это расширит популярность нейросетевых технологий, исключит необходимость специальных знаний. Ведь какие-то начальные возбуждения рецепторов, при их относительном различии, распространятся по нейросети, определяя предпочтительность принимаемого решения! Тогда, на этапе обучения нейросети, получим возможность формирования аналога некой таблицы, в соответствии с которой будет действовать инспектор. (Однако здесь пока не рассматривается процесс обучения нейросети – формирование этой таблицы, а только принцип формирования данных для входа в нее.)

Выделим нейроны, "отвечающие" за типы автомобилей: отечественного производства, "мерседес", "вольво", "джип" и т.д. Величину возбуждения этих нейронов будем полагать равной 1 — на этапе обучения, или равной достоверности события — в рабочем режиме. Аналогично выделим рецепторы, "отвечающие" за другие возможные события: степень интеллигентности водителя (так же по диапазонам изменения), выигрыш или проигрыш любимой команды и т.д.

Следовательно, на входном слое будут формироваться приведенные значения возбуждения.

В рабочем режиме мы, таким образом, получили возможность использования неопределенной, недостоверной информации. Например, инспектор не смог из-за высокой скорости отличить "ниву" от "чероки". Тогда он решает ввести значение 0,5 в графу "нива" (величина возбуждения рецептора, "отвечающего" за "ниву" станет равной 0,5) и 0,5 – в графу "джип "чероки" (такой же станет величина возбуждения соответствующего рецептора). Однако, подумав, он на всякий случай вводит величину 0,2 в графу ВАЗ 2104, что также во власти его сомнений. Так же инспектор поступает и с другими характеристиками сложившейся ситуации в поисках наиболее достоверного решения по принципу наибольшей похожести.

Следует сделать важное замечание. Всегда ли обязательно разбиение параметров, отражаемых непрерывными функциями, на диапазоны изменения? Часто удобно закреплять рецепторы не за диапазонами изменения значений параметров, а за конкретными значениями, наряду с другими объектами, свойствами и др. В этом случае опыт носит дискретный характер.

Например, в этом же примере о штрафовании может быть известен опыт вида:

"Если скорость автомобиля равна 100 км/час & <другие характеристики ситуации>, то размер штрафа составляет..."

"Если скорость автомобиля равна 120 км/час & <другие характеристики ситуации>, то размер штрафа составляет..." и т.д.

Тогда как задать возбуждение рецепторов, если инспектор точно установил, что скорость автомобиля при наезде на пешехода была равна 114 км/час?

По-видимому, он рассуждает на основе близости скорости к границам указанного интервала: "Достоверность того, что скорость автомобиля составляет 100 км/час, я найду как (114 – 100):(120 – 100), а достоверность того, что скорость автомобиля составляет 120 км/час, я найду как (120 – 114):(120 – 100). Следует обратить внимание на то, что сумма найденных достоверностей равна единице.

Таким образом, указан самый простой прием перехода от принадлежности достоверности событий к интервалам – к принадлежности достоверности этих событий к конкретным опытным данным. Этим обеспечивается единообразие отображения объектов любой природы (Вася, Петя), а также булевых переменных вида "да – нет" ("На дворе дождик – или дождика нет").

Следует обратить внимание на то, что в задании исходных данных для логической нейронной сети всегда присутствует фактор волюнтаризма, неопределенности, случайности и даже предвзятости личного мнения. Что ж, не зря же человек – общественное животное.

Пространство признаков

Простейшая система распознавания букв реализуется следующим образом.

Образ буквы, например, а, налагается на входной слой нейросети — рецепторы. Конфигурация возбужденных рецепторов, порождая прохождение возбуждения через внутренние слои нейросети (образуя путь возбуждения), определяет возбуждение (если не гаснет по пути) одного из нейронов выходного слоя, говорящего "это буква а". Интуитивно ясно, что устойчивость такой схемы по отношению к огромному множеству конфигураций возбуждений рецепторов, соответствующих одной только букве а, вряд ли высока. Вглядываясь в себя, мы видим, что такое непосредственное распознавание осуществляется далеко не всегда, особенно — на этапе получения школьного образования, ибо наше образование получается на основе признаков и определений (правил вывода).

Как мы характеризуем строчную букву а? Это кружочек, справа примыкает палочка с хвостиком вправо.

А прописная А? Две палочки с перекладинкой. Но ведь буква Н тоже соответствует этому определению. Тогда мы добавляем: две палочки, соединенные вверху. (Кстати, соединение вверху может быть в результате небрежности лишь обозначено. Тогда о намеке на него мы можем судить по наклону палочек. Дальнейшая небрежность может привести к неразличимости букв А и Н.)

Значит, существует ряд признаков, лежащих в основе определений. И мы, на интуитивном уровне, понимаем, что такой способ распознавания гораздо более устойчив к искажениям и особенностям почерка, однозначен и надежен. Ведь при изображении буквы А можно допустить не только небрежность в верхнем соединении палочек, но и значительную разницу в общем наклоне буквы, в длинах боковых палочек, в месте расположения перекладины, в ее наклоне и длине и т.д. Искажение может привести к сомнениям лишь при крайней похожести на цифру 4, на телеграфный столб или на греческую . Но даже в этом случае окончательный вывод может быть сделан на основе контекста, т.е. по использованию дополнительных признаков "по умолчанию".

Значит, в нашем случае необходимо ввести такие признаки, как наличие кружка, палочек, хвостиков, их взаимного расположения и т.д. То есть, необходимо построить пространство признаков, преобразовать наши входные изображения в это пространство, и тогда появится возможность получения более определенного и устойчивого к искажениям заключения.

Перевод входного изображения в пространство признаков значительно расширяет возможности "разглядывания" — масштабирования, размещения, поиска угла наклона и т.д., т.е. позволяет с более высокой достоверностью производить распознавание.

Например, изображение танка может в разных ракурсах ложиться на входной слой рецепторов. Конечно, можно запомнить, что "и это — танк", "и это — тоже танк" и т.д. Но если ввести хотя бы такое определение, достаточное для соседки — тети Маши, как "массивный корпус на гусеничном ходу (тоже нуждается в определении!), а сверху башня с дулом пушки, и все такое зелененькое", то это научит хотя бы принимать меры предосторожности.