|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Разложение многочленов на неприводимые множители по модулю p. Лемма Гензеля
Обсуждение алгоритма
Выше изложена общая схема алгоритма факторизации, основанного на
разложении полинома над полем  - адических чисел
и на рассмотрении
произведений неприводимых над этим полем множителей. Различные этапы алгоритма
допускают некоторые вариации, часть из которых мы и обсудим.
- адических чисел
и на рассмотрении
произведений неприводимых над этим полем множителей. Различные этапы алгоритма
допускают некоторые вариации, часть из которых мы и обсудим.
18.1. ЗАМЕЧАНИЕ.
Наибольшее количество операций в рассмотренном алгоритме
факторизации требуется при выполнении перебора множителей. Версия алгоритма,
излагаемая Калтофеном в
[
10
]
, предполагает, что старший
коэффициент первого
множителя над полем  совпадает со старшим
коэффициентом исходного
полинома
совпадает со старшим
коэффициентом исходного
полинома ![f(x)\in \mathbb Z[x]](/sites/default/files/tex_cache/8049b0ca71684c4e56d841d8cdedce16.png) . При этом из перебора исключался первый
сомножитель,
перебор осуществлялся по всем подмножествам множества
. При этом из перебора исключался первый
сомножитель,
перебор осуществлялся по всем подмножествам множества  ,
максимальное возможное их количество равно
,
максимальное возможное их количество равно 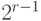 . Если первый
сомножитель
разделить на
. Если первый
сомножитель
разделить на  , что можно выполнить в кольце
, что можно выполнить в кольце  , то достаточно
организовать перебор только по тем подмножествам множества
, то достаточно
организовать перебор только по тем подмножествам множества  ,
которые содержат не более
,
которые содержат не более ![[r/2]](/sites/default/files/tex_cache/5c1cd22cdd8d32270343a731d29db974.png) элементов. В действительности
деление на
элементов. В действительности
деление на  происходит не в кольце
происходит не в кольце  , а в некотором
кольце вычетов
, а в некотором
кольце вычетов  ,
где
,
где  является степенью
является степенью  . Целесообразно,
по-видимому, это деление
выполнять после подъема разложения на неприводимые множители до сравнения по
модулю
. Целесообразно,
по-видимому, это деление
выполнять после подъема разложения на неприводимые множители до сравнения по
модулю  . При этом коэффициенты полинома
. При этом коэффициенты полинома  увеличатся, что
потребует большего времени для выполнения пробных делений, однако более
существенным представляется сокращение времени работы за счет меньшего
количества рассматриваемых вариантов перебора.
увеличатся, что
потребует большего времени для выполнения пробных делений, однако более
существенным представляется сокращение времени работы за счет меньшего
количества рассматриваемых вариантов перебора.
18.2. ЗАМЕЧАНИЕ.
Ограничение вариантов перебора можно организовать не по
максимальному количеству сомножителей, а по максимальной степени делителя.
Достаточно ограничиться степенью ![[n/2]](/sites/default/files/tex_cache/1df61e7f2446684a7a300e9420d62011.png) , где
, где  . При этом
получается лучшее ограничение на необходимую точность разложения
. При этом
получается лучшее ограничение на необходимую точность разложения  .
Количество рассматриваемых вариантов может быть в этом случае существенно
большим.
.
Количество рассматриваемых вариантов может быть в этом случае существенно
большим.
18.3. ЗАМЕЧАНИЕ.
Как отмечалось выше, проверку, представляет ли
произведение  неприводимых над
неприводимых над  полиномов
делитель
полиномов
делитель  в кольце
в кольце ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) , целесообразнее производить путем пробного деления
, целесообразнее производить путем пробного деления  на
на  .
Напомним, что коэффициенты полинома
.
Напомним, что коэффициенты полинома  вычислены с
определенной точностью,
т.е. по модулю некоторого числа
вычислены с
определенной точностью,
т.е. по модулю некоторого числа  , и представлены целыми числами.
Прежде чем
выполнять деление полинома
, и представлены целыми числами.
Прежде чем
выполнять деление полинома  на
на  ,
целесообразно проверить
выполнение некоторых необходимых признаков делимости: например, свободный член
полинома
,
целесообразно проверить
выполнение некоторых необходимых признаков делимости: например, свободный член
полинома  должен делить свободный член полинома
должен делить свободный член полинома  , можно оценить
допустимую величину второго по старшинству коэффициента в
, можно оценить
допустимую величину второго по старшинству коэффициента в  и
сравнить ее
с фактической и т.д.
и
сравнить ее
с фактической и т.д.
18.4. ЗАМЕЧАНИЕ.
В процессе деления полиномов коэффициенты частного могут
получиться по абсолютной величине больше, чем допустимые значения для
коэффициентов
делителя полинома  . В таком случае деление нужно немедленно
прекращать и
переходить к следующей комбинации делителей.
. В таком случае деление нужно немедленно
прекращать и
переходить к следующей комбинации делителей.
18.5. ЗАМЕЧАНИЕ.
При изложении алгоритма уточнения решения мы
пользовались квадратичным подъемом, который позволяет переходить от сравнения
по модулю  к сравнению по модулю
к сравнению по модулю  . Чтобы
избежать многократного
превышения достигнутой точности над требуемой, на последнем шаге можно
ограничиться меньшим значением
. Чтобы
избежать многократного
превышения достигнутой точности над требуемой, на последнем шаге можно
ограничиться меньшим значением  , либо применить линейный подъем.
, либо применить линейный подъем.
18.6. ЗАМЕЧАНИЕ.
Как отмечалось выше, одно из преимуществ использования  - адической метрики состоит в том, что неприводимые по
модулю
- адической метрики состоит в том, что неприводимые по
модулю  многочлены
могут иметь сколь угодно высокие степени. Может возникнуть предположение,
что
для любого полинома
многочлены
могут иметь сколь угодно высокие степени. Может возникнуть предположение,
что
для любого полинома ![f(x)\in \mathbb Z[x]](/sites/default/files/tex_cache/8049b0ca71684c4e56d841d8cdedce16.png) возможно выбрать простое число
возможно выбрать простое число  так, что
разложение
так, что
разложение  по модулю
по модулю  на неприводимые
множители будет совпадать с
разложением
на неприводимые
множители будет совпадать с
разложением  в кольце
в кольце ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) . Эта гипотеза
неверна, можно привести
пример неприводимого в
. Эта гипотеза
неверна, можно привести
пример неприводимого в ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) многочлена сколь угодно большой
степени, который
по модулю любого простого
многочлена сколь угодно большой
степени, который
по модулю любого простого  разлагается на линейные или
квадратичные
множители. Берлекэмпом следующая теорема приписывается
Х.П.Ф. Свиннертону-Дайеру.
разлагается на линейные или
квадратичные
множители. Берлекэмпом следующая теорема приписывается
Х.П.Ф. Свиннертону-Дайеру.
18.7. ТЕОРЕМА. Пусть  - целое число, а
- целое число, а 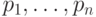 - различные
положительные простые числа. Тогда полином
- различные
положительные простые числа. Тогда полином  со старшим
коэффициентом, равным единице и степени
со старшим
коэффициентом, равным единице и степени  , корни которого равны
, корни которого равны 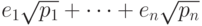 , причем
, причем  для всех
для всех  , имеет
целые коэффициенты и неприводим в
, имеет
целые коэффициенты и неприводим в ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) . Более того, для
любого простого числа
. Более того, для
любого простого числа  полином
полином  по модулю
по модулю  раскладывается на
неприводимые в
раскладывается на
неприводимые в ![\mathbb Z_q[x]](/sites/default/files/tex_cache/be178fa8225448bd4adf244c2de6591b.png) полиномы степени не выше второй.
полиномы степени не выше второй.
Для доказательства теоремы нам потребуется знакомство с основными фактами теории Галуа. Читателю, не знакомому с теорией Галуа, рекомендуется либо ознакомиться с нею, например, просмотрев соответствующую лекцию в монографии ван дер Вардена, либо пропустить доказательство данной теоремы, что можно сделать без существенного ущерба для понимания дальнейшего материала.
ДОКАЗАТЕЛЬСТВО. Пользуемся следующими обозначениями:

Методом математической индукции докажем, что ![f_n (x)\in \mathbb Z[x]](/sites/default/files/tex_cache/5f847c51ee24dd73d61fa5205bcd7b4b.png) ,
, ![[K_n:\mathbb Q ]=2^n](/sites/default/files/tex_cache/ae554bb340c540722af945e7250a0d7a.png) и
и  - примитивный
элемент расширения
- примитивный
элемент расширения 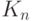 над
над  .
.
Для 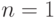 эти факты очевидны.
эти факты очевидны.
Пусть  . Из предположения индукции
. Из предположения индукции ![f_{n-1}(x)\in \mathbb Z[x]](/sites/default/files/tex_cache/c7da0754662191d1c1d4acbb644b18b0.png) и из
соотношения
и из
соотношения  следует, что
следует, что ![f_n(x)\in \mathbb Z[\sqrt{p_n}, x]](/sites/default/files/tex_cache/f733b77a8cc7152cd6e0adc4b944b187.png) , причем коэффициенты
симметричны
относительно
, причем коэффициенты
симметричны
относительно  и
и  . Из
фундаментальной теоремы о
симметрических функциях следует, что эти коэффициенты должны быть целыми. Из
предположения индукции
. Из
фундаментальной теоремы о
симметрических функциях следует, что эти коэффициенты должны быть целыми. Из
предположения индукции ![[K_{n-1}: \mathbb Q ] = 2^{n-1}](/sites/default/files/tex_cache/ddab333cca12831b4ee5e1f953a8fcbf.png) заключаем, что
множество
заключаем, что
множество

 над
над  при
при  .
.Покажем, что  не принадлежит линейному
пространству,
порожденному множеством
не принадлежит линейному
пространству,
порожденному множеством  .
.
Предположим противное. Тогда существуют рациональные числа  , такие, что
, такие, что
 |
( 18.7) |
 , - различные простые
числа, в левой части
равенства (18.7) содержится не менее двух ненулевых
коэффициентов. Тогда
существует
, - различные простые
числа, в левой части
равенства (18.7) содержится не менее двух ненулевых
коэффициентов. Тогда
существует 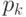 , такое, что в одном из ненулевых слагаемых
содержится
, такое, что в одном из ненулевых слагаемых
содержится  , а в другом - нет. Без потери общности полагаем
, а в другом - нет. Без потери общности полагаем  .
Тогда равенство (18.7) можно переписать в виде
.
Тогда равенство (18.7) можно переписать в виде |
( 18.8) |
 элементов множества
элементов множества  следует, что
следует, что  и
и  . Возведя обе части равенства
(18.8) в квадрат и
выполнив несложные преобразования, получим
. Возведя обе части равенства
(18.8) в квадрат и
выполнив несложные преобразования, получим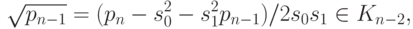
![[K_n: K_{n-1}] = 2](/sites/default/files/tex_cache/d455286bd945dbc268ecc9217a88abd3.png) и
и ![[K_n: \mathbb Q ] = 2^n](/sites/default/files/tex_cache/be0eb0e3597ac74fd62c5a385a0f3896.png) .
.Покажем, что  .
.
Пусть  -
корни полинома
-
корни полинома 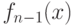 , причем
, причем  . Рассмотрим
полиномы
. Рассмотрим
полиномы 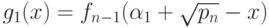 и
и  .
Очевидно, что
.
Очевидно, что ![g_1, g_2\in \mathbb Q (\theta )[x]](/sites/default/files/tex_cache/3073a3cd91be356a18871e1d573d4cd5.png) и имеют
общийкорень
и имеют
общийкорень  .
Однако
.
Однако  , так как все корни полинома
, так как все корни полинома  лежат в
поле
лежат в
поле 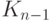 , а
, а  .
Следовательно,
.
Следовательно, ![НОД (g_1,
g_2) = x - \sqrt{p_n}\in \mathbb Q (\theta )[x]](/sites/default/files/tex_cache/ee64e904990e1b021666e94f0331a280.png) , значит
, значит 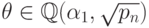 и
и  . По
предположению индукции
. По
предположению индукции  , следовательно,
, следовательно,  . Неприводимость полинома
. Неприводимость полинома  следует теперь из
равенства степени
этого полинома степени расширения над
следует теперь из
равенства степени
этого полинома степени расширения над  , порождаемого его
корнем.
, порождаемого его
корнем.
Свойство разложимости по модулю любого простого числа  выводится из
следующих фактов. Все квадратные корни из элементов
выводится из
следующих фактов. Все квадратные корни из элементов 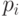 лежат в
некотором
квадратичном расширении поля
лежат в
некотором
квадратичном расширении поля  , a поскольку все
квадратичные расширения
поля
, a поскольку все
квадратичные расширения
поля  изоморфны, то можно считать, что все корни
полинома
изоморфны, то можно считать, что все корни
полинома 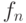 по
модулю
по
модулю  лежат в поле Галуа
лежат в поле Галуа  . Если у
полинома
. Если у
полинома 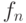 имеется
неприводимый по модулю
имеется
неприводимый по модулю  множитель степени
множитель степени  ,
то его корни порождают
поле
,
то его корни порождают
поле  и не могут быть элементами поля
и не могут быть элементами поля  .
.
18.8. УПРАЖНЕНИЕ
Доказать, что полином  является неприводимым над
является неприводимым над 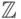 , но разлагается на множители по модулю любого простого
числа
, но разлагается на множители по модулю любого простого
числа  .
.
18.9. УПРАЖНЕНИЕ. Организовать перебор вариантов сомножителей с ограничением по суммарной степени.
18.10. УПРАЖНЕНИЕ.
Пусть ![f(x),g(x)\in\mathbb Z[x]](/sites/default/files/tex_cache/21caededea84000ba0f0e2ab910511ef.png) ,
,  делит
делит  в кольце
в кольце ![\mathbb Q [x]](/sites/default/files/tex_cache/ed65d70295e707093b6ec4334341520d.png) .
Получить оценку для абсолютной величины коэффициента, следующего за
старшим в
.
Получить оценку для абсолютной величины коэффициента, следующего за
старшим в  , через коэффициенты полинома
, через коэффициенты полинома  .
.
