|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Разложение многочленов на неприводимые множители по модулю p. Лемма Гензеля
Лемма Гензеля
Лемма Гензеля в своей классической формулировке, принятой в
алгебре и теории чисел, утверждает, что разложение полинома на взаимно простые
сомножители, выполненное по модулю простого числа  , можно
продолжить до
разложения в кольце
, можно
продолжить до
разложения в кольце  - адических чисел. Доказательство
ее можно найти,
например, в монографии Ван дер Вардена [4 с. 549]. Основу
доказательства
составляет итерационный процесс перехода от сравнения по модулю некоторой
степени числа
- адических чисел. Доказательство
ее можно найти,
например, в монографии Ван дер Вардена [4 с. 549]. Основу
доказательства
составляет итерационный процесс перехода от сравнения по модулю некоторой
степени числа  к сравнению по модулю большей степени
к сравнению по модулю большей степени  . Показывается, что этот
переход можно выполнить за конечное число шагов, вопросам сложности в
алгебраическом доказательстве уделяется мало внимания. Нас же в первую очередь
интересует алгоритм этого перехода с учетом возможности его практической
реализации и оценкой его времени работы.
. Показывается, что этот
переход можно выполнить за конечное число шагов, вопросам сложности в
алгебраическом доказательстве уделяется мало внимания. Нас же в первую очередь
интересует алгоритм этого перехода с учетом возможности его практической
реализации и оценкой его времени работы.
Начнем с изложения леммы Гензеля в простейшем варианте: линейный подъем для двух сомножителей.
Предположим, что ![f(x)\in \mathbb Z[x]](/sites/default/files/tex_cache/3b057447d52d20e6d44e053c770f6a12.png) и по модулю некоторой
степени
и по модулю некоторой
степени  простого числа
простого числа  получено разложение
получено разложение  на взаимно простые
множители:
на взаимно простые
множители:  , где
, где ![g_k,h_k \in
\mathbb Z[x]](/sites/default/files/tex_cache/841ef022b01d5f9d6e34ef82e09583ef.png) . Мы хотим
продолжить это сравнение до сравнения по модулю
. Мы хотим
продолжить это сравнение до сравнения по модулю  .
.
На первом шаге мы должны получить разложение  ,
что достигается применением алгоритма Берлекэмпа. Предположим, что мы нашли
также полиномы
,
что достигается применением алгоритма Берлекэмпа. Предположим, что мы нашли
также полиномы 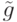 и
и  , такие, что
, такие, что
 |
( 18.1) |
Эти полиномы можно найти, применяя в кольце ![F_p[x]](/sites/default/files/tex_cache/08046df968872bddd17f9de3e18ba88a.png) расширенный алгоритм Евклида к полиномам
расширенный алгоритм Евклида к полиномам  и
и 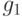 .
Полиномы
.
Полиномы 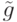 и
и  определены неоднозначно, однозначность получается,
если мы
потребуем, чтобы их степени были ниже степеней полиномов
определены неоднозначно, однозначность получается,
если мы
потребуем, чтобы их степени были ниже степеней полиномов  и
и 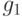 соответственно.
В частности, полиномы
соответственно.
В частности, полиномы 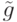 и
и  можно
заменить их остатками от
деления на
можно
заменить их остатками от
деления на  и
и 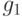 в кольце
в кольце ![F_p[x]](/sites/default/files/tex_cache/08046df968872bddd17f9de3e18ba88a.png)
Более того, без потери общности мы можем предполагать, что старшие
коэффициенты
полиномов  равны
равны  , а старшие коэффициенты
полиномов
, а старшие коэффициенты
полиномов 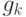 совпадают со
старшим коэффициентом полинома
совпадают со
старшим коэффициентом полинома  . В дальнейшем мы считаем это
условие выполненным,
хотя оно может противоречить выбору систем представителей по
модулю
. В дальнейшем мы считаем это
условие выполненным,
хотя оно может противоречить выбору систем представителей по
модулю 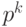 .
.
Полиномы ![g_{k+1},h_{k+1}\in \mathbb Z[x]](/sites/default/files/tex_cache/b83d17cc88151a37f2054ec4f06747c5.png) мы будем искать
в виде
мы будем искать
в виде 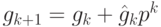 ,
, 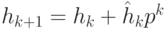 . Сравнения
. Сравнения


Обе части этого сравнения делятся на 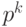 . После деления
получаем сравнение
. После деления
получаем сравнение 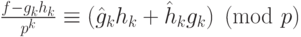 .
В правой части этого сравнения мы можем заменить
.
В правой части этого сравнения мы можем заменить 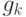 и
и  на
на 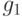 и
и  соответственно. Обозначим
соответственно. Обозначим 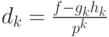 . Домножим
сравнение (18.1) на
. Домножим
сравнение (18.1) на 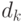 и приравняем коэффициенты
при
и приравняем коэффициенты
при 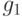 и
и  .
Получим
.
Получим 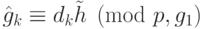 ,
,  .
.
Итак, алгоритм линейного подъема Гензеля можно записать в следующем виде.
А30. АЛГОРИТМ (линейного подъема для двух сомножителей).
![\begin{equation}\\
\text{Дано:\quad$f(x)$, $g_1(x)$,$h_1(x)$, $\tilde g(x)$, $\tilde h(x)\in \mathbb Z[x]$,}\\
\text{\qquad $p \in \mathbb Z$ - простое число, }\\
\text{\qquad $f(x)\equiv g_1(x)h_1(x) \pmod p$,} \\
\text{\qquad $1\equiv g_1(x)\tilde g(x) + h_1(x)\tilde h(x) \pmod
p$, $k\in \N$ }\\
\text{Надо: \qquad $g$ и $h$ такие, что $f(x)\equiv g(x)h(x) \pmod{p^k}$} \\
\text{Начало}\\
\text{$g:=g_1$}\\
\text{$h:=h_1$}\\
\text{цикл для $t$ от $1$ до $k-1$}\\
\text{\qquad $d:=\dfrac{f-g\cdot h}{p^t} \pmod p$}\\
\text{\qquad $g_c:= d\cdot \tilde h \pmod{p, g_1}$}\\
\text{\qquad $h_c:= d\cdot \tilde g \pmod{p, h_1}$}\\
\text{\qquad $g:=g+g_c\cdot p^t$}\\
\text{\qquad $h:=h+h_c\cdot p^t$}\\
\text{конец цикла}\\
\text{Конец}
\end{equation}](/sites/default/files/tex_cache/fc67300a5b7b3b14fda5def92749bc4d.png)
Отметим, что для применения этого алгоритма для произвольного числа сомножителей нужно получить соответствующее представление единицы:
![1\equiv\sum_i\biggl(\prod_{j\ne i}g[j]\biggr)\tilde g[i] \pmod p,](/sites/default/files/tex_cache/3c19bf69de46e96036bfb9a3a6ef8ebe.png)
![\deg\tilde g[i] <\deg g[i]](/sites/default/files/tex_cache/569f1e747d8b8bfec6be52c776f7f901.png) (индекс в квадратных
скобках означает
номер сомножителя).
Один из способов получения такого представления заключается в
поочередном выделении одного из делителей полинома
(индекс в квадратных
скобках означает
номер сомножителя).
Один из способов получения такого представления заключается в
поочередном выделении одного из делителей полинома  и
последовательном
применении расширенного алгоритма Евклида. Другой способ — искать
полиномы
и
последовательном
применении расширенного алгоритма Евклида. Другой способ — искать
полиномы ![\tilde g[i] \pmod p](/sites/default/files/tex_cache/83d6a14ce6ac04680230648cdfe0e99f.png) в кольце
в кольце ![F_p[x]](/sites/default/files/tex_cache/08046df968872bddd17f9de3e18ba88a.png) методом неопределенных
коэффициентов. Относительно этих коэффициентов получается система линейных
уравнений порядка
методом неопределенных
коэффициентов. Относительно этих коэффициентов получается система линейных
уравнений порядка  , условие невырожденности которой
совпадает с
условием, что полиномы
, условие невырожденности которой
совпадает с
условием, что полиномы ![g[i]](/sites/default/files/tex_cache/e6a43ae58299bf21c6e781a53f6de017.png) не имеют общих делителей. (Нетрудно
заметить, что
нам нужно решить задачу, эквивалентную разложению дроби
не имеют общих делителей. (Нетрудно
заметить, что
нам нужно решить задачу, эквивалентную разложению дроби \bigr)} \pmod
p](/sites/default/files/tex_cache/768ebb0346c9b8568f8c34c7f5c8b263.png) в сумму простейших.)
в сумму простейших.)Снова предполагаем, что старший коэффициент полинома ![g[1]](/sites/default/files/tex_cache/32c7b7ee09ff69598c04c8233a896f31.png) совпадает со
старшим коэффициентом полинома
совпадает со
старшим коэффициентом полинома  , а старшие коэффициенты
остальных
сомножителей
, а старшие коэффициенты
остальных
сомножителей ![g[i]](/sites/default/files/tex_cache/e6a43ae58299bf21c6e781a53f6de017.png) равны
равны  .
.
