|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Разложение многочленов на неприводимые множители по модулю p. Лемма Гензеля
Пример вычисления матрицы Q и нахождения ее нуль- пространства.
Данный пример взят из монографии Кнута [ 9 ] .
Пусть

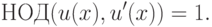
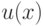 свободен от квадратов. Далее,
свободен от квадратов. Далее,  ,
следовательно, 1-я строка матрицы
,
следовательно, 1-я строка матрицы  равна
равна  .
Вычислим вторую строку, т.е.
.
Вычислим вторую строку, т.е.  .
Ниже приводятся вычисления.
.
Ниже приводятся вычисления.
Получили вторую строку матрицы  , записанную в обратном
порядке. Продолжая подобным образом, получим остальные строки
матрицы
, записанную в обратном
порядке. Продолжая подобным образом, получим остальные строки
матрицы  :
:

Вычитая единичную матрицу, получим

Переходим к нахождению нуль-пространства.
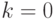 . Первая строка нулевая, таким образом,
получаем собственный вектор
. Первая строка нулевая, таким образом,
получаем собственный вектор ![v[1] = (1, 0,\dots, 0)](/sites/default/files/tex_cache/03b3db8a9fc9053cb33d9fb98481e268.png) .
.
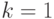 . В качестве допустимого значения
. В качестве допустимого значения  можно взять
любое
можно взять
любое  (напомним, что нумерация
столбцов начинается с 0). Удобно взять
(напомним, что нумерация
столбцов начинается с 0). Удобно взять  , т.к.
, т.к.  . Прибавляя к
. Прибавляя к  -му
столбцу
-му
столбцу 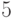 -ый столбец, умноженный на
-ый столбец, умноженный на 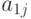 ,
,  ,
получим
,
получим

Продолжая таким же образом, получим
 ,
, 

 ,
, 

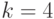 ,
, 

 ,
, 

Таким образом, матрица приведена к ступенчатому виду. Для нахождения
собственных векторов
в качестве свободных параметров выбираем последние две координаты. При этом
получаются векторы ![v[2] = (0, 5, 5, 0, 9, 5, 1, 0)](/sites/default/files/tex_cache/5476ee387e396d51ef0a154dc5ba0d51.png) и
и ![v[3] = (0, 9, 11, 9, 10, 12, 0, 1)](/sites/default/files/tex_cache/2dabe45a7b27269d62822b5b3c0cd0e7.png) .
.
Им соответствуют многочлены
 &= x^6+5x^5+9x^4+5x^2+5x, \\
v[3](x) &=x^7+12x^5+10x^4+9x^3+11x^2+9x.
\end{align*}](/sites/default/files/tex_cache/632ae0af6dc150d14a7d6d9a578f9ee7.png)
Находим  - s)](/sites/default/files/tex_cache/6a7f4a3e125c76d472380e47f15e6a9d.png) . Получаем
. Получаем
 - 0) &=x^5+5x^4+9x^3+5x+5, \\
НОД(u(x), v[2](x) - 2) &=x^3+8x^2+4x+12.
\end{align*}](/sites/default/files/tex_cache/f99c5f381e906e517c12736e7e093e8c.png)
 , отличных от 0 и 2, получаем
, отличных от 0 и 2, получаем -s) = 1](/sites/default/files/tex_cache/be925b80767d027246bc4084e99c54a4.png) . Поскольку при приведении матрицы
. Поскольку при приведении матрицы  к ступенчатому виду мы получили
к ступенчатому виду мы получили  ,
продолжаем поиск неприводимых множителей. Находим, что
при
,
продолжаем поиск неприводимых множителей. Находим, что
при 
 - s, x^5+5x^4+9x^3+5x+5)
=x^4+2x^3+3x^2+4x+6,](/sites/default/files/tex_cache/664791156ed33c19fe5578cff9e409a7.png)
-s, x^5+5x^4+9x^3+5x+5) = x + 3,](/sites/default/files/tex_cache/55e2444b8550384403e43bb0fea4f178.png)
 этот
этот  равен 1.
равен 1.Таким образом, мы нашли все три неприводимых сомножителя, на которые
исходный многочлен 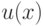 разлагается в поле вычетов по модулю 13.
разлагается в поле вычетов по модулю 13.
