|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Базисы Гребнера
10.7. ОПРЕДЕЛЕНИЕ.
Мы говорим, что многочлен  инволютивно
редуцируется к многочлену
инволютивно
редуцируется к многочлену  с помощью многочлена
с помощью многочлена  по моному m и пишем, опуская упоминание о мономе
по моному m и пишем, опуская упоминание о мономе  ,
, ![f\xrightarrow[\text{inv}h]{}g](/sites/default/files/tex_cache/c155eccedeeec17952d93d2d52c5784e.png) ,
если
,
если  редуцируется к
редуцируется к  в обычном смысле, и
в обычном смысле, и 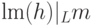 .
Естественным образом определяется отношение
.
Естественным образом определяется отношение ![\xrightarrow[\text{inv
}G]{}](/sites/default/files/tex_cache/adc1fae543c4db6221657a7649df9991.png) для произвольного множества
для произвольного множества  многочленов и его транзитивное
многочленов и его транзитивное ![\smash[b]{\xrightarrow[\text{inv
}G]+}](/sites/default/files/tex_cache/47037bfec8b55eda9aa082f869a73a56.png) и рефлексивно-транзитивное
и рефлексивно-транзитивное ![\xrightarrow[\text{inv }G]*](/sites/default/files/tex_cache/ee7b10085b21628c9d63b36e3c9e735d.png) замыкания.
замыкания.
Если задано отношение редукции, то определена нормальная форма, которая в данном случае называется инволютивной.
Немультипликативным продолжением многочлена будем называть его произведение на некоторую немультипликативную для его старшего монома переменную.
10.8. ПРИМЕР.
Пусть 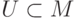 - конечное подмножество. Для каждого
- конечное подмножество. Для каждого 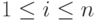 разделим множество
разделим множество  на группы,
помеченные неотрицательными
целыми числами
на группы,
помеченные неотрицательными
целыми числами 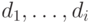 :
:
![[d_1,\ldots,d_i]=\{u\in U\sep d_j=\deg_j(u),\;1\le j\le
i\}.](/sites/default/files/tex_cache/5acde7c2fe609a30c2fbe7c07efe88bd.png)
 мультипликативна для
мультипликативна для 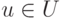 ,
если
,
если 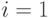 и
и 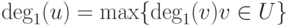 , или
, или  ,
, ![u\in[d_1,\ldots,d_{i-1}]](/sites/default/files/tex_cache/bd43a633f9d85aaca2c63a6d780e0d61.png) и
и ![\deg_i(u)=
\max\{\deg_i(v)\sep
v\in[d_1,\ldots,d_{i-1}]\}](/sites/default/files/tex_cache/fe36617304a228585a82b6e830f226cb.png) .
(Здесь
.
(Здесь  обозначает степень по переменной
обозначает степень по переменной  .)
.)10.9. ОПРЕДЕЛЕНИЕ.
Пусть ![R=K[x_1,\dots,x_m]](/sites/default/files/tex_cache/b6d8cf66323a51c626f97e239f026b38.png) - кольцо многочленов от переменных
- кольцо многочленов от переменных  ,
,  - идеал кольца
- идеал кольца  ,
,  - конечное множество и
- конечное множество и  - инволютивное деление
на множестве мономов
- инволютивное деление
на множестве мономов  .
Множество
.
Множество  называется инволютивным базисом
идеала
называется инволютивным базисом
идеала  , если
для любого ненулевого элемента
, если
для любого ненулевого элемента  имеется инволютивное представление
имеется инволютивное представление
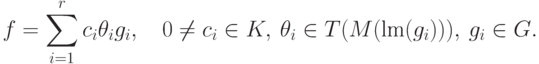 |
( 10.1) |
10.10. ТЕОРЕМА. Пусть ![R=K[x_1,\dots,x_m]](/sites/default/files/tex_cache/b6d8cf66323a51c626f97e239f026b38.png) - кольцо многочленов от переменных
- кольцо многочленов от переменных  ,
,  - идеал кольца
- идеал кольца  ,
,  - конечное множество и
- конечное множество и  - инволютивное деление
на множестве мономов
- инволютивное деление
на множестве мономов  . Предположим, что множество
. Предположим, что множество  нормализовано таким
образом, что
нормализовано таким
образом, что  для всех
для всех  .
Тогда эквивалентны
следующие условия:
.
Тогда эквивалентны
следующие условия:
-
 является инволютивным базисом идеала
является инволютивным базисом идеала  ;
; -
 инволютивно порождает
инволютивно порождает 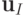 ;
; - для любого
 имеет место
имеет место ![f\xrightarrow[\text{inv
}G]* 0](/sites/default/files/tex_cache/2f30fde26c66af3f316bc9cb4c4b6141.png) ;
; - если
 и
и  инволютивно нередуцируемы,
то
инволютивно нередуцируемы,
то  ;
; - если
 и
и  инволютивно нередуцируем, то
инволютивно нередуцируем, то 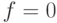 . Следующие условия являются необходимыми для выполнения предыдущих, и если
множество
. Следующие условия являются необходимыми для выполнения предыдущих, и если
множество  порождает
порождает  , то они являются и
достаточными:
, то они являются и
достаточными: - Если
 и
и 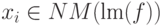 , то
, то 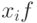 допускает инволютивное представление;
допускает инволютивное представление; -
![x_if\xrightarrow[\text{inv }G]*0](/sites/default/files/tex_cache/8fb9d5fb37eaa5deb2bbc002b0f9048b.png) для любых
для любых  и
и 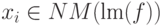 .
.
Доказательство оставляется читателю в качестве упражнения.
Инволютивный базис может быть легко построен, если мы знаем авторедуцированный базис Гребнера соответствующего идеала и инволютивное деление. Это построение сводится к домножению элементов базиса Гребнера на немультипликативные переменные.
Имея инволютивный базис 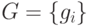 и инволютивное деление,
можно построить алгоритм нормальной формы следующим образом:
для каждого многочлена
и инволютивное деление,
можно построить алгоритм нормальной формы следующим образом:
для каждого многочлена  образуем множество его инволютивных
кратных
образуем множество его инволютивных
кратных  ; множество
; множество  является
базисом
линейного пространства
является
базисом
линейного пространства  , причем любой моном может присутствовать
не более, чем в одном элементе этого базиса. Для любого
многочлена
, причем любой моном может присутствовать
не более, чем в одном элементе этого базиса. Для любого
многочлена  мы можем исключать те его слагаемые, которые
присутствуют в качестве старших
мономов в множестве инволютивных кратных. Легко показать, что нередуцируемый
многочлен, получающийся после таких исключений, не
зависит от порядка этих исключений. Однако, чтобы избежать повторных
исключений одного и того же монома (сразными
коэффициентами), естественно проводить эти действия в порядке убывания
мономов. Таким образом мы получаем алгоритм нормальной
формы.
мы можем исключать те его слагаемые, которые
присутствуют в качестве старших
мономов в множестве инволютивных кратных. Легко показать, что нередуцируемый
многочлен, получающийся после таких исключений, не
зависит от порядка этих исключений. Однако, чтобы избежать повторных
исключений одного и того же монома (сразными
коэффициентами), естественно проводить эти действия в порядке убывания
мономов. Таким образом мы получаем алгоритм нормальной
формы.
Естественно, не всякий алгоритм нормальной формы может быть получен таким образом. Возникает задача описания тех алгоритмов нормальной формы, которые определяются с помощью инволютивных базисов.
10.11. ПРЕДЛОЖЕНИЕ. Если множество старших мономов многочленов из идеала разбивается на непересекающиеся конусы так, что элементы одного конуса редуцируются по одному многочлену из базиса, то соответствующее инволютивное деление выглядит следующим образом: для вершины конуса мультипликативными являются переменные, соответствующие образующим, а внутри конуса деление задается произвольным образом.
ДОКАЗАТЕЛЬСТВО.
Формально указанное инволютивное деление 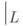 задается так:
пусть
задается так:
пусть 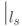 - произвольное инволютивное деление,
соответствующее конусу
- произвольное инволютивное деление,
соответствующее конусу 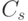 с вершиной в мономе
с вершиной в мономе  .
Положим
.
Положим
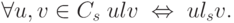
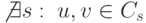 , то положим
, то положим  .
Положим
.
Положим 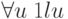 .
Аксиомы инволютивного деления выполнены:
.
Аксиомы инволютивного деления выполнены:-
 ;
; -
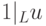 - по определению
- по определению  ;
; -
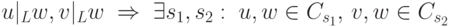 , но тогда
, но тогда 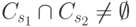 , значит,
, значит, 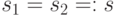 . Отсюда
. Отсюда 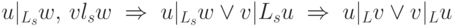 ;
; 
-
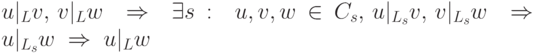 .
.
По определению  , любой старший моном многочлена
идеала инволютивно редуцируется к вершине соответствующего конуса,
кроме того, инволютивная нормальная форма всегда единственна.
Алгоритм нормальной формы, заданный этими конусами, устроен так же.
Поэтому соответствие алгоритма нормальной формы и инволютивного
деления установлено.
, любой старший моном многочлена
идеала инволютивно редуцируется к вершине соответствующего конуса,
кроме того, инволютивная нормальная форма всегда единственна.
Алгоритм нормальной формы, заданный этими конусами, устроен так же.
Поэтому соответствие алгоритма нормальной формы и инволютивного
деления установлено.
