НОУ ИНТУИТ | Введение в компьютерную алгебру. Лекция 2: Проблема представления данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 04.03.2008 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 28 студентам

| Поделиться |

Поддержать программу

Многочлены

Действия с многочленами лежат в основе любой системы компьютерной алгебры. Пусть K — некоторое кольцо, задача представления элементов которого уже решена. Представление элементов кольца многочленов K[x] можно выбирать различными способами. Наиболее распространенным является представление многочлена в виде последовательности коэффициентов, упорядоченной по возрастанию или убыванию степеней одночленов. Представление многочленов, при котором запоминаются все коэффициенты, включая нулевые, называется плотным. Плотное представление используется в задачах, где рассматриваемые многочлены имеют сравнительно небольшое количество нулевых коэффициентов. Если степени многочленов достаточно высоки, а количество ненулевых коэффициентов мало ( разреженные многочлены ), то удобнее использовать разреженное представление многочленов, в котором указываются только ненулевые коэффициенты и соответствующие степени одночленов. При этом алгоритмы работы с такой формой записи становятся более сложными, но значительно экономится память ЭВМ, а во многих случаях—и время работы программы.

Приведенная выше форма представления многочленов в случае, когда кольцо коэффициентов является полем, основана на том факте, что одночлены составляют базис кольца многочленов, рассматриваемого как бесконечномерное векторное пространство над полем коэффициентов. В некоторых случаях целесообразно использовать другие базисы этого пространства. Например, в "Базисы Гребнера" изучаются многочлены вида $\binom{x+k}k=\frac{(x+k)(x+k-1)\dots(x+1)}{k!},$ обладающие многими полезными свойствами. Часто оказывается полезным представление многочленов фиксированной степени набором значений в разных точках.

Многочлены от многих переменных можно рекурсивно рассматривать как многочлены от одной переменной, но с коэффициентами из кольца многочленов от меньшего числа переменных ( рекурсивное представление ). А можно на множестве одночленов ввести отношение порядка и записывать слагаемые в соответствии с выбранным порядком. Наиболее часто используются следующие три отношения порядка:

лексикографическое упорядочение мономов, получающееся из фиксированного порядка на множестве переменных;
упорядочение мономов по степеням, а мономы одной и той же степени упорядочиваются лексикографически;
упорядочение мономов по степеням, а мономы одной и той же степени упорядочиваются в обратном лексикографическом порядке, т. е. при равенстве степеней большим считается вектор с меньшей последней координатой, при равенстве последних координат — с меньшей предпоследней и т. д. Может показаться, что этот порядок совпадает с предыдущим, для "отраженных" векторов. При n = 2 это действительно так, однако в общем случае эти два отношения порядка различаются более существенно, что продемонстрировано в примере 3.1б), где предполагается, что x > y > z

Более подробно вопросы, связанные с упорядочением мономов и каноническим представлением многочленов от нескольких переменных, будут рассмотрены ниже в разделе, посвященном базисам Гребнера.

3.1. ПРИМЕРЫ.

Пусть переменные x и y упорядочены так, что x > y. Тогда многочлен (x + y)² + x + y + 1 с учетом соответствующих порядков записывается в виде:
(лексикографический порядок);

(по степени, затем лексикографический);

(по степени, затем обратный лексикографический).
Рассмотрим разложение многочлена (x+y+z)³. Из однородности многочлена следует, что первые два из рассматриваемых порядков для этого многочлена совпадают. Выпишем его представление с использованием второго и третьего порядка.
и

соответственно.

Можно пользоваться как плотной (когда записываются все коэффициенты от самого старшего до самого младшего или наоборот), так и разреженной (когда записываются только ненулевые коэффициенты и соответствующие степени) формой записи. В отличие от многочленов от одной переменной, для которых используется как разреженное, так и плотное представление, для многочленов от нескольких переменных плотное представление почти не применяется, поскольку уже при сравнительно небольших степенях количество коэффициентов в этих многочленах весьма велико и почти все они нулевые.

Отметим, что достаточно часто при действии с многочленами предпочтительнее пользоваться представлениями, отличными от канонического. Например, во многих отношениях запись (x + y + z)³ более удобна, чем приведенные выше разложения этого многочлена. В частности, для многочленов задача разложения на множители представляет еще большую сложность, чем для целых чисел, и поэтому не всегда целесообразно раскрывать при умножении скобки,- часто бывает полезным в ущерб каноничности записи хранить многочлен в виде произведения.

Рациональные функции.

Поле рациональных функций K(x₁, . . . , x_n), где K - некоторое поле, обычно определяется как поле частных кольца многочленов K[x₁, . . . , x_n]. Имея каноническое представление элементов кольца многочленов, каноническое представление рациональных функций можно получить наложением условия взаимной простоты числителя и знаменателя и нормировкой знаменателя (например, приравниванием старшего коэффициента знаменателя единице). 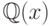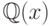Часто, однако, поле K само представляется как поле частных некоторой области целостности, например, поле $\mathbb Q(x)$ можно представить как поле частных кольца $\mathbb Q[x]$ , а также как поле частных кольца $\mathbb Z[x]$ . При представлении поля $\mathbb Q(x)$ как поля частных кольца $\mathbb Z[x]$ далеко не всегда можно в представлении рациональной функции приравнять старший коэффициент знаменателя единице. Множество обратимых элементов в Z состоит всего из двух элементов ( 1 и -1 ), и нормировку знаменателя можно осуществить, фиксируя знак старшего коэффициента.