Проблема представления данных

Кольцо целых чисел

Из курса программирования известно, что целое число может быть представлено в памяти компьютера разными способами, в частности, это представление зависит от того, как оно описано: как величина типа integer, или real, или string. При этом в большинстве языков программирования под целыми числами понимаются числа из весьма ограниченного диапазона: типичный случай — от -2¹⁵ = -32768 до 2¹⁵ - 1 = 32767. Системы компьютерной алгебры имеют дело с большими целыми числами, в частности, любая такая система умеет вычислять и выводить в десятичной записи числа вида 1000! (более тысячи знаков).

В данном курсе мы будем рассматривать представление целых чисел в символьном виде и не вдаваться в подробности, какая память отводится для записи одного символа (бит, байт или другая). Наиболее распространенным является представление целых чисел в позиционных системах счисления. Такая система определяется выбором основания счисления, например, 10. Множество десятичных целых чисел обычно описывается следующим образом:

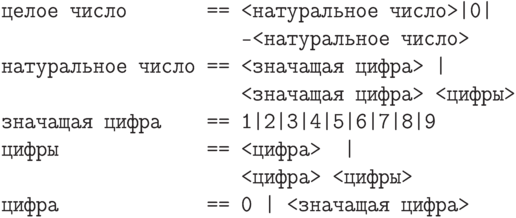
Выписанное определение целых чисел дает однозначность представления каждого такого числа, и аналогичное определение (только, может быть, с другим основанием) используется в большинстве систем компьютерной алгебры. Пользуясь таким представлением, удобно реализовать арифметические операции над целыми числами. При этом сложение и вычитание являются относительно "дешевыми" операциями, а умножение и деление — "дорогими" . При оценке сложности арифметических операций следует учитывать как стоимость элементарной операции (одноразрядной), так и количество одноразрядных операций для выполнения какого-либо действия над многозначными числами. Сложность умножения и деления обусловлена, в первую очередь, тем, что с ростом длины числа (его записи в какой-либо системе счисления) количество элементарных операций увеличивается по квадратичному закону, в отличие от линейного для сложения и вычитания. К тому же, то, что мы обычно называем алгоритмом деления многозначных чисел, в действительности основано на переборе (часто весьма значительном) возможной очередной цифры частного, и при этом недостаточно просто воспользоваться правилами деления однозначных чисел. При большом основании системы счисления (часто оно может иметь порядок 2³⁰ ) этот способ малоэффективен.

Пусть — натуральное число (записанное в десятичной системе). Чтобы получить его запись 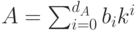в -ичной системе счисления, можно воспользоваться следующим алгоритмом ( обозначает целую часть числа ):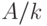

Дано: A—натуральное число в десятичной системе счисления
	k > 1—натуральное число
Надо: A—запись числа A в k-ичной системе счисления

Начало
i := 0
цикл пока A > 0
	bi := A (mod k)
	A := [A/k]
	i := i + 1
конец цикла
dA := i - 1
Конец

Для восстановления десятичного числа по последовательности 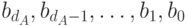его k -ичной записи 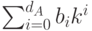используется следующий алгоритм:

Дано: k > 1—натуральное число
	последовательность цифр, представляющих число A
	в k-ичной системе
Надо: A—запись числа A в десятичной системе счисления

Начало
A := 0
цикл пока не конец последовательности
	b := очередной элемент последовательности
	A := A * k + b
конец цикла
Конец

1.2. УПРАЖНЕНИЕ. Объясните, почему для перевода числа из десятичной системы в k -ичную используется деление, а для перевода из k -ичной системы в десятичную — умножение.

Перемножая "столбиком" два двузначных числа в десятичной системе счисления, мы выполняем следующие операции:

(10a + b)(10c + d) = 100ac + 10(ad + bc) + bd,

т. е. 4 операции умножения одноразрядных чисел, 3 операции сложения и 2 операции умножения на степень основания счисления, которые сводятся к сдвигу. При оценке сложности можно учитывать все элементарные операции, не разделяя их по весам (в данном примере мы имеем 9 элементарных операций). Задача оптимизации алгоритма сводится при данном подходе к минимизации общего числа элементарных операций. Можно, однако, считать, что умножение является более "дорогой" операцией, чем сложение, которое, в свою очередь, "дороже" сдвига. Учитывая только наиболее дорогие операции, мы получаем, что мультипликативная сложность умножения двузначных чисел "столбиком" равна 4.

В параграфе 5 рассматриваются алгоритмы вычисления наибольших общих делителей и оценивается их сложность.

Рассмотренное представление не является единственным каноническим представлением целых чисел. Как уже отмечалось, для выбора канонического представления можно воспользоваться единственностью разложения натурального числа на простые множители. Такое представление целого числа может быть применено в тех задачах, где используются только операции умножения и деления, так как они становятся очень "дешевыми" , однако несоизмеримо возрастает стоимость операций сложения и вычитания, что препятствует использованию подобного представления. В некоторых задачах отказ от канонического представления дает значительный выигрыш в быстродействии, в частности, может использоваться частичное разложение числа на множители. Особенно полезен аналогичный метод при работе не с числами, а с многочленами.

Если известно, что при работе программы все встречающиеся в вычислениях целые числа ограничены по абсолютной величине некоторой заданной константой, то можно использовать для задания таких чисел их систему вычетов по модулям некоторых взаимно простых чисел, произведение которых превосходит упомянутую константу. Вычисления с классами вычетов выполняются, как правило, быстрее, чем арифметика многократной точности. А арифметикой многократной точности при таком подходе нужно пользоваться только при вводе или выводе информации.

Отметим, что наряду с каноническими представлениями в системах компьютерной алгебры используются и другие представления. В частности, желательно, чтобы наличие или отсутствие знака '+' перед целым числом не влияло на восприятие его компьютером. Таким образом, для положительных чисел получается неоднозначное представление, хотя форма отрицательных чисел определена однозначно.

Другое требование — на восприятие числа не должно влиять наличие нулей перед первой значащей цифрой.

1.3. УПРАЖНЕНИЯ.

1. Оценить количество одноразрядных умножений, используемых при умножении столбиком m -значного числа на n - значное.
2. Показать, что два двузначных числа можно перемножить, используя только 3 умножения однозначных чисел и увеличив число сложений.
3. Найти алгоритм деления длинных чисел, не требующий большого перебора при нахождении первой цифры частного.
4. Описать алгоритм перевода натуральных чисел из m -ичной системы счисления в n -ичную.
5. В римской нумерации для записи чисел используются следующие символы: I — единица, V — пять, X — десять, L — пятьдесят, C — сто, D — пятьсот, M — тысяча. Символ считается отрицательным, если правее него найдется символ большего числа, и положительным в противном случае. Например, число 1948 в этой системе запишется так: MCMXLVIII. Сформулировать алгоритм перевода числа из римской записи в десятичную и обратно. Реализовать полученный алгоритм на одном из алгоритмических языков (например, C ). Ограничения на исходные данные: 1 <= N < 3700, в записи результата ни один символ не должен появляться больше 3 раз.
6. Сформулировать алгоритм и написать программу сложения натуральных чисел в римской нумерации.
7. Будем говорить, что мы имеем дело с системой счисления со смешанным или векторным основанием, если нам задан вектор из n натуральных чисел M = (m₁, . . . ,m_n) (осно вание счисления) и запись K = (k₀, k₁, . . . , k_n) обозначает число k = k₀+m₁(k₁+m₂(k₂+· · ·+m_n ·k_n) . . . )). Написать программу, которая по данным (день недели, часы, минуты, секунды) определяет, сколько секунд прошло с начала недели (понедельник, 0, 0, 0) = 0, и выполняет обратное преобразование.