|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Проблема представления данных
Целые p-адические числа.
p -адические числа играют значительную роль в теории чисел, и для более подробного знакомства с ними читателю следует обратиться к литературе по теории чисел, например к книге [ 3 ] . Здесь мы только приведем основные определения и некоторые свойства p -адических чисел.
2.1. ОПРЕДЕЛЕНИЕ. Пусть p — некоторое простое число. Последовательность целых чисел
{xn} = {x0, x1, . . . , xn, . . . },обладающая тем свойством, что
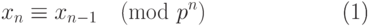 |
( 2.1) |
для всех n >= 1, определяет новый объект, называемый целым p - адическим числом. Две последовательности {xn} и 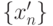 тогда и только тогда определяют одно и то же целое p -адическое число, когда
тогда и только тогда определяют одно и то же целое p -адическое число, когда  для всех n >= 0.
для всех n >= 0.
В отличие от целых p -адических чисел, обычные целые числа часто называют целыми рациональными.
Каждому целому рациональному числу x можно сопоставить целое p -адическое число, определяемое последовательностью
{x, x, . . . , x, . . . }.Это p -адическое число будем обозначать той же буквой x. Множество целых p -адических чисел будем обозначать Op.
Укажем способ, при помощи которого из всех последовательностей, определяющих одно и то же p -адическое число, можно выбрать одну стандартную.
Пусть {xn} — целое p -адическое число. Обозначим через 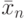 наименьшее неотрицательное число, сравнимое с xn по модулю pn+1, т. е.
наименьшее неотрицательное число, сравнимое с xn по модулю pn+1, т. е.
 |
( 2.2) |
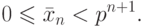 |
( 2.3) |
Для любого целого p -адического числа {xn}, последовательность, все члены которой удовлетворяют условиям (2.2) и (2.3), будем называть канонической.
Ставя в соответствие каждому целому p -адическому числу его каноническую последовательность, мы получаем взаимно однозначное соответствие между множеством целых p -адических чисел и множеством последовательностей вида
{a0, a0 + a1p, a0 + a1p + a2p2, . . . , },где 0 <= ai < p.
2.2. ОПРЕДЕЛЕНИЕ. Суммой и произведением целых p -адических
чисел  и
и 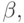 определяемых последовательностями {xn} и {yn}, называются целые p -адические числа, определяемые соответственно
последовательностями {xn + yn} и {xnyn}.
определяемых последовательностями {xn} и {yn}, называются целые p -адические числа, определяемые соответственно
последовательностями {xn + yn} и {xnyn}.
2.3. УПРАЖНЕНИЕ. Показать, что введенные выше операции определены корректно и превращают Op в коммутативное кольцо с единицей.
Сформулируем несколько теорем, доказательство которых оставляется читателю в качестве упражнения (их можно найти, например, в [ 3 ] ).
2.4. ТЕОРЕМА. Целое p -адическое число 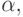 определяемое последовательностью {x0, x1, . . . , xn, . . . }, тогда и только тогда является единицей (т. е. обратимым) в Op, когда
определяемое последовательностью {x0, x1, . . . , xn, . . . }, тогда и только тогда является единицей (т. е. обратимым) в Op, когда 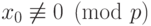 .
.
2.5. ТЕОРЕМА. Всякое отличное от нуля целое p -адическое число  однозначно представляется в виде
однозначно представляется в виде
 |
( 2.4) |
2.6. ТЕОРЕМА. Для любого натурального n, всякое целое p -адическое число сравнимо с целым рациональным числом по модулю pn. Два целых рациональных числа тогда и только тогда
сравнимы по модулю pn в кольце Op, когда они сравнимы по этому модулю в кольце  .
.
2.7. ОПРЕДЕЛЕНИЕ. Число m в представлении (2.4) отличного от
нуля целого p -адического числа  называется p -показателем числа
называется p -показателем числа  и обозначается
и обозначается 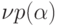 .
.
Индекс p в определении показателя мы будем часто опускать
и говорить просто о показателе, обозначая его 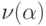 . Доопределим
показатель, полагая
. Доопределим
показатель, полагая 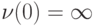 . Непосредственно проверяется, что
. Непосредственно проверяется, что
 |
( 2.5) |
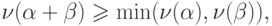 |
( 2.6) |
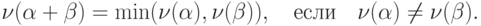 |
( 2.7) |

 —
—