| Россия |
Оптимизационные модели
4.4.Планирование штатного расписания
Планирование штатного расписания относится к типу задач оптимального распределения трудовых ресурсов.
Задача 4.6.
Необходимо укомплектовать штат работников в диспетчерской фирме в соответствии со следующими требованиями: каждый день недели должно работать определенное количество работников (см. таблицу). При этом служащие должны иметь два выходных дня. В каждой группе – не менее 2 человек. Руководитель фирмы заинтересован в экономии заработной платы. Обеспечить работу в течение недели фирмы в соответствии с ресурсным планом при минимальном фонде заработной платы.
Потребность в работниках каждый день недели
Постановка задачи.
Организуем группы, каждая из которых имеет свои выходные дни - два смежных дня. У первой группы выходные - Вс и Пн., у второй - Пн и Вт. и т.д. Всего - 7 групп. Дневная оплата каждой группы приведена в таблице. Задача – определить количество работников в каждой группе при минимальной суммарной оплате.
| № группы | Вых.дни | Количество работников | Оплата P. |
| 1 | Вс.,Пн. | х1 | 50 |
| 2 | Пн. Вт. | х2 | 45 |
| 3 | Вт. Ср. | х3 | 45 |
| 4 | Ср. Чт. | х4 | 45 |
| 5 | Чт. Пт. | х5 | 45 |
| 6 | Пт. Суб. | х6 | 55 |
| 7 | Суб. Вс | х7 | 50 |
Модель задачи.
-
Выбираем объекты для моделирования: и исходные данные - т.е. что мы имеем.
- плановое количество работников на каждый день недели
- выходные для работников – два смежных дня,
- дневная оплата работника постоянна,
- минимизация общей оплаты работников.
- Детализируем объекты, применяя системный подход. Учитываем все данные.
Входные переменные:
-
 – текущий день недели,
– текущий день недели, -
 – текущий номер группы.
– текущий номер группы.  –количество групп
–количество групп -
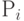 – оплата одного работника в
– оплата одного работника в  группе
группе -
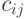 - параметр, обозначающий выход на работу
- параметр, обозначающий выход на работу  группы в
группы в  день недели, выход –
день недели, выход –  , выходной –
, выходной –  (см. таблицу 4.7).
(см. таблицу 4.7).
| Группа | Вс. | Пн. | Вт. | Ср. | Чт. | Пт. | Сб. |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 3 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 4 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 5 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 6 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
Управляемые переменные –  - количество работников в
- количество работников в  группе,
группе,
Ограничения
Ресурсное -  - количество работающих в j день недели
- количество работающих в j день недели
Плановое –  требуемое количество работников в
требуемое количество работников в  группе .
группе .
Выходные показатели – суммарная заработная плата  .
.
Целевая функция – результирующий, оптимизируемый параметр – суммарная заработная плата минимальна.

В результате имеем систему уравнений.
 |
( 4.11) |
Решение. Данные вводятся в виде матриц. Матрица выхода бригад на работу двумерна. Задача решается с помощью блока  и функции
и функции  . Документ Mathcad решения задачи показан ниже.
. Документ Mathcad решения задачи показан ниже.


 - номер группы,
- номер группы,  – день недели
– день недели
Потребности работников: 
Решение:
Начальные значения:
 – количество работников
– количество работников






Ограничение: 
Потребности работников


Ограничение:





