НОУ ИНТУИТ | Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования. Лекция 4: Оптимизационные модели

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 27.05.2014 | Уровень: для всех | Доступ: платный | ВУЗ: Уральский государственный экономический университет

|

Вам нравится? Нравится 25 студентам

| Поделиться |

Поддержать программу

4.3. Транспортная задача

Транспортная задача – задача поиска оптимального распределения поставок однородных грузов [20]. В общей постановке формулируется так: составить план поставок продукции (грузов) от поставщиков к потребителям, имеющий минимальную стоимость затрат.

Модель задачи.

Входные переменные:

–количество поставщиков, – текущий номер поставщика.
- количество потребителей , – текущий номер потребителя,
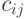$c_{ij}$ - стоимость перевозки единицы продукции от - го поставщика к -му потребителю, $A_i(i=\overline{1,m})$ - объемы производства поставщиков,
$B_j(j=\overline{1,n})$ – объемы доставки продукции от всех поставщиков потребителям,
$Р_{ij}$ – требуемое количество единиц продукта, доставленного от - го поставщика к -му потребителю при наличии плана доставки

Управляемые переменные - 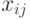$x_{ij}$ - количество единиц продукта, доставленного от - го поставщика к -му потребителю,

Выходные показатели – суммарные затраты доставки продукции $F=\sum_{i=1}^{m}\sum_{j=1}^{n}c_{ij}x_{ij}$ .

Целевая функция – результирующий, оптимизируемый параметр – суммарные затраты. Цель решения задачи – нахождение значений управляемых переменных 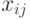$x_{ij}$ , обеспечивающих минимум целевой функции .

$F=\sum_{i=1}^{m}\sum_{j=1}^{n}c_{ij}x_{ij}\to \min$

Математическая модель транспортной задачи может быть закрытой (сбалансированной) - все грузы должны быть вывезены, и все потребности полностью удовлетворены. В этом случае $\sum_{i}^{m}A_i=\sum_{j}^{n}B_j$ .

На практике обычно встречается случай открытой (несбалансированной) транспортной задачи, когда производство не совпадает с потреблением. В этом случае открытая модель сводится к закрытой. Для этого вводятся либо фиктивный поставщик (случай дефицита), либо фиктивный потребитель (случай перепроизводства). Стоимость перевозок единицы продукции, как от фиктивного поставщика, так и до фиктивного потребителя полагают раной нулю, так как в обоих случаях продукция не перевозится.

$\sum_{i}^{m}A_i-\sum_{j}^{n}B_j=объем \;продукции\; фиктивного\; поставщика\; (потребителя)$

При добавлении фиктивного поставщика (потребителя) количество поставщиков (или потребителей ) увеличивается на единицу.

В результате имеем систему уравнений.

$\left\{ \begin{array}{lc} \sum_{i=1}^{m}x_{ij}=A_i \; (i=\overline{1,m}) \\ \sum_{j=1}^{n}x_{ij}=A_j \; (j=\overline{1,n}) \\ x_j\ge 0, \; i=\overline{1,m}, \; j=\overline{1,n} \\ x_j\ge P_j \\ F=\sum_{i=1}^{m}\sum_{j=1}^{n}c_{ij}x_{ij}\to \min \\ \end{array} \right\$

( 4.8)

Открытая транспортная задача

Задача 4.4.

Имеется 4 мебельные фирмы и 5 центров распределения товаров - магазинов. Планируется наладить перевозки продукции с фирм в магазины. Фирмы имеют следующие возможности производства: 280, 150, 225, 175 единиц в месяц. Пяти магазинам необходимо поставить 100, 200, 50, 250 и 150 единиц товара в месяц соответственно. Необходимо так спланировать перевозки, чтобы уменьшить (оптимизировать) транспортные расходы.

Стоимость перевозок единиц продукции приведена в таблице.

Таблица 4.3. Стоимость перевозки единицы продукции
Фирмы/магазины	Олимп	Сфера	Квартира	Уют	Товары для дома
Томек	1,50	2	2,25	2,25	2,25
СуперМебель	2,5	2,2	1,65	1	1,5
Мебель-лес	2,3	1,7	1,5	1,4	1,6
ЦентрМебель	2,3	0,5	1,85	1,35	1,25

Решение (рис. 4.4). Определим тип задачи. Суммарное количество производимого товара составляет $\sum_{i}^{m}A_i=830$ , количество товара, которое надо доставить $\sum_{j}^{n}B_j=750$ . Задача "открытого типа". Имеем случай перепроизводства. Сбалансируем задачу, сведем к "закрытому типу", введя фиктивного потребителя с потребностью $\sum_{i}^{m}A_i-\sum_{j}^{n}B_j=80$ . Стоимость перевозок единицы продукции до фиктивного потребителя считаем равной нулю.

В Mathcad транспортная задача решается аналогично задаче производства – в матричном виде, с помощью блока given и в данном случае функции miniimize . Особенность заключается в том, что матрица неизвестных двумерна. Для построения ограничений – нахождения суммы по строкам и по столбцам вводим единичные векторы. . Порядок действий тот же. Документ Mathcad решения задачи показан на рис.4.3.

ORIGIN:=1

Входные данные

$m:=4, \; n:=5$

$\underline{i}:=1..\underline{m}$ - фирмы-поставщики

$\underline{j}:=1..\underline{n}$ - магазины-потребители

Производство фирм поставщиков: $A:=\begin{pmatrix} 280\\ 150\\ 225\\ 175 \end{pmatrix}$

Потребность магазинов: $B:=\begin{pmatrix} 100\\ 200\\ 50\\ 250\\ 150\end{pmatrix}$

$\sum_{\underline{i}}^{}\underline{A}_{\underline{i}}=830$ , $\sum_{\underline{j}}^{}\underline{B}_{\underline{j}}=750$ , $\sum_{\underline{i}}^{}\underline{A}_{\underline{i}}-\sum_{\underline{j}}^{}\underline{B}_{\underline{j}}=80$

Вводим фиктивного потребителя в магазин с потребностью 80 ед.

$\underline{n}:=\underline{n}+1=6$ , $\underline{j}:=1..\underline{n}$

$\underline{Потребители}+\underline{фиктивный}$

$B:=\begin{pmatrix} 100\\ 200\\ 50\\ 250\\ 150\\ 80\end{pmatrix}$

Стоимость перевозки ед. продукции: $с:=\begin{pmatrix} 1.5 & 2 & 1.55 & 2.25 & 2.25 & 0\\ 2.5 & 2.2 & 1.65 & 1 & 1.5 & 0 \\ 2.3 & 1.7 & 1.5 & 1.4 & 1.6 & 0\\ 2.3 & 0.5 & 1.85 & 1.35 & 1.25 & 0\end{pmatrix}$

Решение:

$\underline {F}(\underline {x})=\sum_{\underline {i}=1}^{m}\sum_{\underline {j}=1}^{\underline {n}}(\underline {x}_{\underline {i}\underline {j}}\cdot \underline {c}_{\underline {i}\underline {j}})$

Начальные значения: $\underline{x}_{\underline {i},\underline {j}}:=1$

Единичный вектор-столбец для магазинов: $\underline{v}_{\underline {j}}:=1$

Единичный вектор-столбец для поставщиков: $\underline {k}_{\underline {j}}:=1$

$\underline{Given}$

$\underline{x}\cdot \underline{v}=\underline{A}$

$\underline{x}^T\cdot \underline{k}=\underline{B}$

$x \ge 0$

$\underline{x}:=\underline{Minimize}(\underline{F}, \underline{x})$

Оптимальные перевозки: $x=\begin{pmatrix} 100 & 25 & 50 & 0 & 25 & 80\\ 0 & 0 & 0 & 150 & 0 & 0 \\ 0 & 0 & 0 & 100 & 125 & 0\\ 0 & 175 & 0 & 0 & 0 & 0\end{pmatrix}$

Затраты: $\underline {F}(\underline {x})=911.25$

$\underline {x}\cdot \underline {y}=\begin{pmatrix} 280\\ 150\\ 225\\ 175 \end{pmatrix}$

$\underline {x}^T\cdot \underline {k}=\begin{pmatrix} 100\\ 200\\ 50\\ 250 \\ 150 \\ 80\end{pmatrix}$

Рис. 4.3. Листинг решения задачи 4.4. Оптимальные перевозки. Показан фиктивный потребитель.

Результат решения показывает, как спланировать доставку. Минимальные затраты составляют F=911ед. Излишек товара выгоднее отправить в "Товары для дома" (магазин 5).

Дальше >>

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

Оптимизационные модели

4.3. Транспортная задача

Открытая транспортная задача

Вопросы и ответы

Студенты

Авторизоваться

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

Оптимизационные модели

4.3. Транспортная задача

Открытая транспортная задача

Вопросы и ответы

Студенты