НОУ ИНТУИТ | Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования. Лекция 4: Оптимизационные модели

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 27.05.2014 | Уровень: для всех | Доступ: платный | ВУЗ: Уральский государственный экономический университет

|

Вам нравится? Нравится 25 студентам

| Поделиться |

Поддержать программу

Транспортная задача с промежуточными пунктами

Есть транспортные задачи, в которых пункты отправления и назначения являются промежуточными, через них переправляются товары в конечный пункт назначения. В данной постановке промежуточные пункты выступают и как потребители и как поставщики. В данном случае формируется единая транспортная матрица, в которой количество поставщиков и количество потребителей увеличивается на число промежуточных пунктов.

Задача 4.5.

Усложним условия задачи 4.4. Фирмы производят и вывозят мебель на 3 склада. Необходимо распределить доставку товаров от поставщиков на склады, со складов в магазины по заказам так, чтобы оптимизировать транспортные расходы. Фирмы производят 280, 150, 225, 175 единиц. Вместимость складов 400, 300, 350 единиц. Магазины заказывают 100, 200, 50, 250 и 150 единиц товара, соответственно. Стоимость перевозок единиц продукции с фирм на склады и со склада в магазины приведена в таблице 4.4, таблице 4.5.

Таблица 4.4. Стоимость перевозки единицы продукции с фирм на склады
Фирмы	Склад 1	Склад 2	Склад 3	Объемы производства на фирмах
Фирма 1	2,4	3,0	2,3	280
Фирма 2	3,9	3,2	4,3	150
Фирма 3	3,3	3,3	2,1	225
Фирма 4	4,3	2,7	3,2	175
Вместимость складов	400	300	350

Таблица 4.5. Стоимость перевозки единицы продукции со складов в магазины
Склады	"Олимп"	"Сфера"	"Квартира"	"Уют"	"Товары для дома"
Склад 1	5,8	3,9	3,6	5,4	2,8
Склад 2	4,8	5,5	3,3	2,0	2,0
Склад 3	2,2	3,3	3,6	3,4	1,6
Потребности	100	200	50	250	150

Модель задачи.

В модель задачи. добавляется входная переменная склады - три склада $D_k\; (k=\overline{1,s}),\; s=3$ . Склады выступают и как потребители, и как поставщики. Формируется единая матрица, в которой количество элементов поставщиков и количество потребителей увеличивается на число складов: строки = поставщики плюс склады, столбцы = склады плюс магазины. Для запрета перевозок со склада на другой склад и непосредственно от поставщиков в магазины устанавливается очень большой, нереальный тариф (999999).

Таблица стоимости доставки со склада на склад имеет вид:

	Склад 1	Склад 2	Склад 3
Склад 1	0	999999	999999
Склад 2	999999	0	999999
Склад 3	999999	999999	0

Таблица стоимости доставки со склада в магазин имеет вид:

Фирмы	"Олимп"	"Сфера"	"Квартира"	"Уют"	"Товары для дома"
Фирма 1	999999	999999	999999	999999	999999
Фирма 2	999999	999999	999999	999999	999999
Фирма 3	999999	999999	999999	999999	999999
Фирма 4	999999	999999	999999	999999	999999

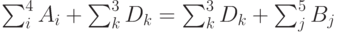Задача решается в объединенной матрице. $M_{i+k, k+j}$ стоимость доставки в объединенной матрице стоимостей. Баланс устанавливается по сумме производства поставщиков и емкости складов, с одной стороны, и емкости складов и потребности магазинов, с другой стороны. $\sum_{i}^{4}A_i+\sum_{k}^{3}D_k=\sum_{k}^{3}D_k+\sum_{j}^{5}B_j$ .

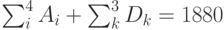Здесь $\sum_{i}^{4}A_i+\sum_{k}^{3}D_k=1880$ , $\sum_{k}^{3}D_k+\sum_{j}^{5}B_j=1800$ данной задаче необходим фиктивный потребитель с потребностью 80 ед. В остальном модель аналогична предыдущей модели. Система уравнений:

$\left\{ \begin{array}{lc} \sum_{i=1}^{m+s}x_{ij}=A_i(i=\overline{1,m})+D_k(k=\overline{1,s}) \\ \sum_{j=1}^{n+s}x_{ij}=B_j(j=\overline{1,n})+D_k(k=\overline{1,s}) \\ x_j\ge 0, \; i=\overline{1,m+s}, \; j=\overline{1,n+s} \\ F=\sum_{i}^{n+s}\sum_{j}^{m+s}M_{ij}\cdot x_{ij}\to \min \\ \end{array} \right\$

( 4.10)

Решение. В Mathcad задача строится аналогично транспортной задаче. Данные вводятся в матричном виде, оптимизация реализуется с помощью блока given и функции minimize , ограничения вводятся с единичные векторы. Здесь ообенность заключается в том, строится объединенная матрица. Для этого используем встроенные функции для матричных операций

Функция augment (M1, M2) объединяет в одну матрицы 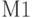и , имеющие одинаковое число строк.

Функция stack (M1, M2) объединяет в одну матрицы 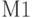и , имеющие одинаковое число столбцов. (см. Приложение 2). Документ Mathcad решения задачи показан ниже.

ORIGIN:=1

Входные данные

$\underline{i}:=1..4$ - фирмы-поставщики

$\underline{j}:=1..5$ - магазины-потребители

$\underline{k}=1..3$ - склады

Производство фирм поставщиков: $A:=\begin{pmatrix} 280\\ 150\\ 225\\ 175 \end{pmatrix}$

Емкость складов: $D:=\begin{pmatrix} 400\\ 300\\ 350 \end{pmatrix}$

Потребность магазинов: $B:=\begin{pmatrix} 100\\ 200\\ 50\\ 250\\ 150\end{pmatrix}$

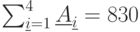$\sum_{\underline{i}=1}^{4}\underline{A}_{\underline{i}}=830$ , $\sum_{\underline{k}=1}^{3}\underline{D}_{\underline{k}}=1050$ , $\sum_{\underline{j}=1}^{5}\underline{B}_{\underline{j}}=750$

$\underline{поставщики}+\underline{склады}$ : $\sum_{\underline{i}}^{}\underline{A}_{\underline{i}}+\sum_{\underline{k}}^{}\underline{D}_{\underline{k}}=1880$

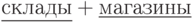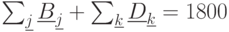
$\underline{склады}+\underline{магазины}$ : $\sum_{\underline{j}}^{}\underline{B}_{\underline{j}}+\sum_{\underline{k}}^{}\underline{D}_{\underline{k}}=1800$

Вводим фиктивного потребителя в магазин с потребностью 80 ед.

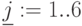$\underline{j}:=1..6$ , $\underline{j}:=1..\underline{n}$

$\underline{магазины}+\underline{фиктивный}$

$\underline {B}:=\begin{pmatrix} 100\\ 200\\ 50\\ 250 \\ 150 \\ 80\end{pmatrix}$

Стоимость перевозки ед. продукции от фирмы на склад: $с:=\begin{pmatrix} 2.4 & 3 & 2.3 \\ 3.9 & 3.2 & 4.3 \\ 3.3 & 3.3 & 2.1\\ 4.3 & 2.7 & 3.2 \end{pmatrix}$

Стоимость перевозки ед. продукции со склада в магазин: $с:=\begin{pmatrix} 5.8 & 3.9 & 3.6 & 5.4 & 2.8 & 0 \\ 4.8 & 5.5 & 3.3 & 2.0 & 2.0 & 0 \\ 2.2 & 3.3 & 3.6 & 3.4 & 1.6 & 0 \end{pmatrix}$

Решение

матрица стоимостей фиктивной доставки со склада на склад: $underline{cc}:=\begin{pmatrix} 0 & 999999 & 999999 \\ 999999 & 0 & 999999 \\ 999999 & 999999 & 0 \end{pmatrix}$

матрица стоимостей фиктивной доставки с фирмы в магазин: 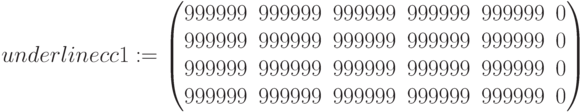$underline{cc1}:=\begin{pmatrix} 999999 & 999999 & 999999 & 999999 & 999999 & 0 \\ 999999 & 999999 & 999999 & 999999 & 999999 & 0 \\ 999999 & 999999 & 999999 & 999999 & 999999 & 0 \\ 999999 & 999999 & 999999 & 999999 & 999999 & 0 \end{pmatrix}$

Объединяем матрицы: $\underline{M1}:=\underline{argument}(\underline{c},\underline{cc1})$ , $\underline{A1}:=\underline{stack}(\underline{A},\underline{D})$

$\underline{M2}:=\underline{argument}(\underline{cc},\underline{c1})$ , $\underline{B1}:=\underline{stack}(\underline{D},\underline{B})$

$\underline {A1}:=\begin{pmatrix} 280\\ 150\\ 225\\ 175\\ 400\\ 300 \\ 350 \end{pmatrix}$ , $\underline {B1}:=\begin{pmatrix} 400\\ 300\\ 350\\ 100\\ 200\\ 50\\ 250 \\ 150 \\ 80\end{pmatrix}$

$\underline {M1}:=\begin{pmatrix} 2.4 & 3 & 2.3 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 0\\ 3.9 & 3.2 & 4.3 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 0\\ 3.3 & 3.3 & 2.1 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 0 \\ 4.3 & 2.7 & 3.2 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 10\times 10^5 & 0 \end{pmatrix}$

$\underline {M2}:=\begin{pmatrix} 0 & 10\times 10^5 & 10\times 10^5 & 5.8 & 3.9 & 3.6 & 5.4 & 2.8 & 0\\ 10\times 10^5 & 0 & 10\times 10^5 & 4.8 & 5.5 & 3.3 & 2 & 2 & 0\\ 10\times 10^5 & 10\times 10^5 & 0 & 2.2 & 3.3 & 3.6 & 3.4 & 1.6 & 0 \end{pmatrix}$

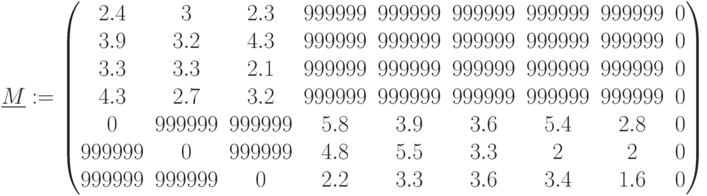
$\underline{M}:=\underline{stack}(\underline{M1},\underline{M2})$ , $\underline {M}:=\begin{pmatrix} 2.4 & 3 & 2.3 & 999999 & 999999 & 999999 & 999999 & 999999 & 0\\ 3.9 & 3.2 & 4.3 & 999999 & 999999 & 999999 & 999999 & 999999 & 0\\ 3.3 & 3.3 & 2.1 & 999999 & 999999 & 999999 & 999999 & 999999 & 0 \\ 4.3 & 2.7 & 3.2 & 999999 & 999999 & 999999 & 999999 & 999999 & 0 \\ 0 & 999999 & 999999 & 5.8 & 3.9 & 3.6 & 5.4 & 2.8 & 0\\ 999999 & 0 & 999999 & 4.8 & 5.5 & 3.3 & 2 & 2 & 0\\ 999999 & 999999 & 0 & 2.2 & 3.3 & 3.6 & 3.4 & 1.6 & 0\end{pmatrix}$

$i:=1..7.\; j:=1..9$

Начальные значения: $x_{i,j}:=1$

Единичный вектор для строк и столбцов $v1_i:=1,\; v2_j:=1$

$F(x):=\sum_{i=1}^{7}\sum_{j=1}^{9}(x_{i,j}\cdot M_{i,j})$

Civen

$x^T\cdot v1=B1$

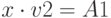
$x\cdot v2=A1$

$x\ge 0$

Оптимальные перевозки: x:=Minimize(F,x)

Затраты: F(x)=26000065

Ограничения:

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline 1& 113 & 13 & 35 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 2 & 4 & 18 & 49 & 0 & 0 & 0 & 0 & 0 & 9 \\ \hline 3 & 110 & 78 & 37 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 4 & 100 & 18 & 56 & 0 & 0 & 0 & 0 & 0 & 1 \\ \hline 5 & 73 & 0 & 0 & 39 & 94 & 42 & 27 & 126 & 0 \\ \hline 6 & 0 & 54 & 0 & 10 & 81 & 8 &137 & 9 & 0\\ \hline 7 & 0 & 0 & 173 & 51 & 25 & 0 & 86 & 15 & 0 \\ \hline \end{array}$

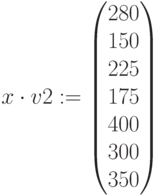$x\cdot v2:=\begin{pmatrix} 280\\ 150\\ 225\\ 175\\ 400\\ 300 \\ 350 \end{pmatrix}$ , $x^T\cdot v1:=\begin{pmatrix} 400\\ 300\\ 350\\ 100\\ 200\\ 50\\ 250 \\ 150 \\ 80\end{pmatrix}$

Рис. 4.4. Диаграмма доставки

Дальше >>

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

Оптимизационные модели

Транспортная задача с промежуточными пунктами

Вопросы и ответы

Студенты

Авторизоваться

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

Оптимизационные модели

Транспортная задача с промежуточными пунктами

Вопросы и ответы

Студенты