Информационные технологии
Необходимые и достаточные условия существования префиксного кода с заданными длинами кодовых слов. Неравенство Крафта
Для применения кода на практике желательно, чтобы кодовые слова были как можно короче. Однако чем слова короче, тем их запас меньше. В этом легко убедиться, посмотрев на изображение словарного универсума на рис.6.3. Если попытаться построить префиксный код с очень короткими длинами кодовых слов, то можно потерпеть неудачу - кода с такими длинами слов может не быть. Например, нетрудно убедиться, что не существует префиксного кода с длинами слов 1, 1, 2. При необходимости построить префиксный код с большим числом кодовых слов заданной длины проверка существования такого кода может быть достаточно сложной. К счастью, найдены необходимые и достаточные условия на длины кодовых слов для существования префиксного и любого однозначно декодируемого кода. Эти условия известны как теорема Крафта - Макмиллана. Необходимые и достаточные условия сформулируем в виде двух теорем.
Теорема (необходимые условия). Пусть 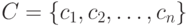 - префиксный двоичный код с длинами кодовых слов
- префиксный двоичный код с длинами кодовых слов 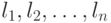 . Тогда выполняется неравенство Крафта
. Тогда выполняется неравенство Крафта
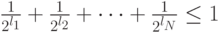 |
( 6.3) |
Доказательство. Рассмотрим, сколько слов длины  может быть в префиксном коде. Максимальное число таких слов равно
может быть в префиксном коде. Максимальное число таких слов равно 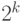 . В этом случае все
. В этом случае все 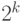 кодовых слова имеют длину
кодовых слова имеют длину  .
.
Для каждого кодового слова длины  имеется
имеется 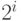 слов длины
слов длины  , для которых данное слово является префиксом и по этой причине не является кодовым. Это следует из структуры словарного дерева (см. рис. 6.3). Множества
, для которых данное слово является префиксом и по этой причине не является кодовым. Это следует из структуры словарного дерева (см. рис. 6.3). Множества 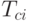 и
и 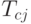 слов длины
слов длины  , для которых кодовые слова
, для которых кодовые слова  и
и 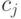 являются префиксами, не пересекаются, так как в противном случае более короткое из этих слов было бы префиксом более длинного. Значит, если в префиксном коде имеется
являются префиксами, не пересекаются, так как в противном случае более короткое из этих слов было бы префиксом более длинного. Значит, если в префиксном коде имеется 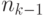 слов длины
слов длины 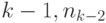 слов длины
слов длины 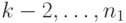 слов длины 1, то число
слов длины 1, то число 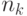 слов длины
слов длины  удовлетворяет неравенству
удовлетворяет неравенству
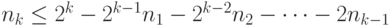 |
( 6.4) |
Это неравенство верно для любого  , в том числе и для
, в том числе и для  , равного максимальной длине кодовых слов. После деления на
, равного максимальной длине кодовых слов. После деления на 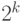 обеих частей неравенства (6.4) его можно преобразовать к виду
обеих частей неравенства (6.4) его можно преобразовать к виду
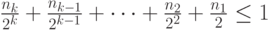 |
( 6.5) |
Слагаемое вида 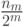 , представляющее в неравенстве (6.5)
, представляющее в неравенстве (6.5) 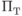 кодовых слов длины
кодовых слов длины  , можно записать в виде суммы
, можно записать в виде суммы
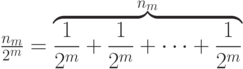
С учетом такого представления неравенство (6.5) можно переписать следующим образом:
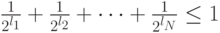
где  - общее число слов префиксного кода. Теорема доказана.
- общее число слов префиксного кода. Теорема доказана.
Выполнение неравенства Крафта доказано для префиксного кода. Однако в 1956 году Макмиллан доказал более общую теорему, согласно которой неравенство Крафта выполняется и для любого однозначно декодируемого кода. Доказательство теоремы изложено в [29], [31].
Можно также доказать, что если префиксный код полный, то в нестрогом неравенстве (6.3) будет выполняться равенство.
Теорема (достаточные условия). Если положительные целые числа 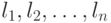 удовлетворяют неравенству Крафта
удовлетворяют неравенству Крафта
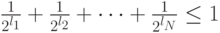
то существует префиксный код 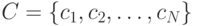 с длинами кодовых слов
с длинами кодовых слов 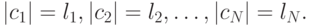
Доказательство. Если среди чисел 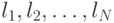 имеется ровно
имеется ровно 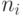 чисел, равных
чисел, равных  , то неравенство Крафта можно записать в виде
, то неравенство Крафта можно записать в виде
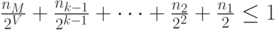
где  - максимальное из данных чисел. Из справедливости этого неравенства следует, что верны неравенства (6.5) для всех
- максимальное из данных чисел. Из справедливости этого неравенства следует, что верны неравенства (6.5) для всех  , а следовательно, и неравенство (6.4).
, а следовательно, и неравенство (6.4).
Для построения нужного префиксного кода должна быть возможность подходящим образом выбрать  слов длины 1,
слов длины 1, 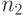 слов длины 2, вообще
слов длины 2, вообще 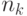 слов длины
слов длины 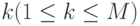 или, иными словами,
или, иными словами,  вершин кодового дерева на первом,
вершин кодового дерева на первом, 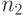 - на втором,
- на втором, 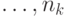 - на
- на  -м ярусе.
-м ярусе.
Из неравенства (6.4) при 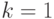 получаем
получаем  , т. е. требуемое число не превосходит общего числа вершин первого яруса. Значит, на этом ярусе можно выбрать какие-то
, т. е. требуемое число не превосходит общего числа вершин первого яруса. Значит, на этом ярусе можно выбрать какие-то  вершин в качестве концевых (
вершин в качестве концевых ( равно 0, 1 или 2). Если это сделано, то из общего числа вершин второго яруса (их
равно 0, 1 или 2). Если это сделано, то из общего числа вершин второго яруса (их 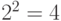 ) для построения кода можно использовать лишь
) для построения кода можно использовать лишь 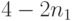 . Однако и этого числа вершин хватит, так как из неравенства (6.4) при
. Однако и этого числа вершин хватит, так как из неравенства (6.4) при  вытекает
вытекает
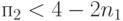
Аналогично, при  имеем неравенство:
имеем неравенство:
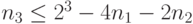
Правая часть его вновь совпадает с допустимым для построения префиксного кода числом вершин третьего яруса, если на первых двух ярусах уже выбраны  и
и 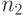 кодовых вершин. Значит, снова можно выбрать
кодовых вершин. Значит, снова можно выбрать 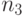 кодовых вершин на третьем ярусе. Продолжая этот процесс вплоть до
кодовых вершин на третьем ярусе. Продолжая этот процесс вплоть до 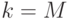 , мы и получим требуемый код. Теорема доказана.
, мы и получим требуемый код. Теорема доказана.
Докажем, что если для длин 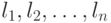 кодовых слов выполняется равен - равенство
кодовых слов выполняется равен - равенство 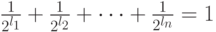 ,то код является полным. Предположим противное, то есть, что код не полный. Тогда к нему можно добавить, по крайней мере, одно кодовое слово (длины
,то код является полным. Предположим противное, то есть, что код не полный. Тогда к нему можно добавить, по крайней мере, одно кодовое слово (длины 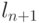 ) и получить новый префиксный код, для которого, с одной стороны,
) и получить новый префиксный код, для которого, с одной стороны, 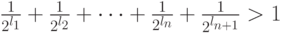 , а с другой стороны, в силу теоремы Крафта,
, а с другой стороны, в силу теоремы Крафта, 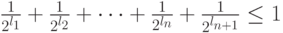 Полученное противоречие доказывает утверждение.
Полученное противоречие доказывает утверждение.
Теоремы Крафта доказаны для случая, когда рассматриваются коды в алфавите  . Если кодовый алфавит содержит
. Если кодовый алфавит содержит  символов, то аналогичным образом можно доказать, что необходимым и достаточным условием для существования префиксного кода с длинами слов
символов, то аналогичным образом можно доказать, что необходимым и достаточным условием для существования префиксного кода с длинами слов 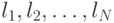 является выполнение неравенства
является выполнение неравенства
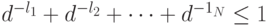
Оказывается, этому неравенству обязаны удовлетворять и длины кодовых слов произвольного однозначно декодируемого кода. Поэтому, если существует однозначно декодируемый код с длинами слов 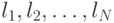 , то существует и префиксный код с теми же длинами слов.
, то существует и префиксный код с теми же длинами слов.
Методы построения кодов. Код Фано
Один из методов алфавитного кодирования был предложен Фано. Схема кодирования по методу Фано заключается в следующем. Предположим, что кодируемые сообщения источника (знаки исходного алфавита) располагаются в последовательности 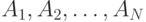 так, что соответствующие им вероятности не возрастают, т. е.
так, что соответствующие им вероятности не возрастают, т. е. 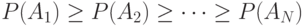 . Рассмотрим разбиения последовательности A 1, A2, …, AN на две подпоследовательности
. Рассмотрим разбиения последовательности A 1, A2, …, AN на две подпоследовательности 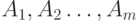 и
и 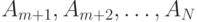 Каждое такое разбиение определяется числом
Каждое такое разбиение определяется числом 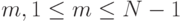 , которое определяет, сколько элементов исходной последовательности входит в первую и вторую части разбиения. Среди
, которое определяет, сколько элементов исходной последовательности входит в первую и вторую части разбиения. Среди 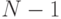 разбиения выберем такое, чтобы модуль разности
разбиения выберем такое, чтобы модуль разности 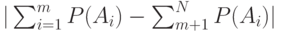 был минимальным. Всем сообщениям из первой части разбиения в качестве первого знака кодового слова приписываем 0, а сообщениям из второй части 1. По тому же принципу каждая из полученных подпоследовательностей снова разбивается на две части, и это раз-биение определяет значение второго символа кодового слова. Процедура продолжается до тех пор, пока все множество не будет разбито на отдельные сообщения. В результате каждому из сообщений будет сопоставлено кодовое слово из нулей и единиц.
был минимальным. Всем сообщениям из первой части разбиения в качестве первого знака кодового слова приписываем 0, а сообщениям из второй части 1. По тому же принципу каждая из полученных подпоследовательностей снова разбивается на две части, и это раз-биение определяет значение второго символа кодового слова. Процедура продолжается до тех пор, пока все множество не будет разбито на отдельные сообщения. В результате каждому из сообщений будет сопоставлено кодовое слово из нулей и единиц.
Описанную процедуру построения кода Фано на примере из пяти сообщений иллюстрирует следующая таблица.
| Сообщения | Вероятности сообщений | Знаки кодовых слов | Кодовое слово | ||
|---|---|---|---|---|---|
| 1-й знак | 2-й знак | 3-й знак | |||
 |
0.4 | 0 | 0 | 00 | |
 |
0.15 | 1 | 01 | ||
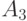 |
0.15 | 1 | 0 | 10 | |
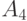 |
0.15 | 1 | 0 | 110 | |
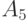 |
0.15 | 1 | 111 | ||
Понятно, что чем более вероятно сообщение, тем быстрее оно образует "самостоятельную" группу и тем более коротким словом оно будет закодировано. Это обстоятельство и обеспечивает высокую экономность кода Фано. Код, построенный для данного источника методом Фано, имеет среднюю длину кодового слова равную 2,3.
Код, построенный методом Фано, всегда является префиксным. Действительно, на первом шаге построения кода методом Фано множество сообщений источника разбивается на два подмножества. Все кодовые слова, соответствующие первому подмножеству, имеют однобуквенный префикс, состоящий из 0, а все слова, соответствующие второму подмножеству, имеют однобуквенный префикс, состоящий из 1 (или наоборот). Поэтому ни одно слово, соответствующее какому-нибудь из сообщений из первого подмножества, не может быть префиксом ни для какого слова, соответствующего сообщению из второго подмножества. Аналогичная процедура разбиения применяется к каждому подмножеству сообщений с одинаковыми префиксами при добавлении нового знака к формируемым кодовым словам. При этом число подмножеств, на которые разбивается исходное множество сообщений источника (блоков разбиения), увеличивается. Важным свойством разбиений является то, что для кодовых слов, соответствующих сообщениям из разных блоков разбиения, имеются различные префиксы. Построение кода завершается разбиением множества сообщений на блоки, содержащие по одному сообщению. Из-за отмеченного свойства разбиений ни одно кодовое слово не является префиксом другого кодового слова, то есть построенный методом Фано код является префиксным.
Описанный метод кодирования можно применять и в случае произвольного алфавита из  символов, с той лишь разницей, что на каждом шаге следует производить разбиение на
символов, с той лишь разницей, что на каждом шаге следует производить разбиение на  равновероятных групп.
равновероятных групп.
Избыточность кодирования. Нижняя граница средней длины кодирования
Рассмотренные ранее примеры показывают, что использование кодов переменной длины позволяет эффективнее кодировать сообщения по сравнению с равномерным кодированием. Для получения оценки минимально достижимой средней длины кодового слова рассмотрим избыточность кодирования 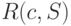 , представляющую собой разность
, представляющую собой разность 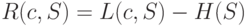 между средней длиной кодового слова при кодировании источника S кодом c и энтропией. Две следующие теоремы показывают, какова нижняя граница средней длины кодирования и как близко можно приблизиться к этой границе за счет рационального выбора кодовых слов.
между средней длиной кодового слова при кодировании источника S кодом c и энтропией. Две следующие теоремы показывают, какова нижняя граница средней длины кодирования и как близко можно приблизиться к этой границе за счет рационального выбора кодовых слов.
Для доказательства первой теоремы напомним одно свойство логарифма, которое заключается в том, что график функции  лежит ниже касательной к ней в точке
лежит ниже касательной к ней в точке 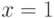 , и следовательно, выполняется неравенство
, и следовательно, выполняется неравенство 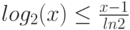 . Это свойство иллюстрирует рис.6.6.
. Это свойство иллюстрирует рис.6.6.
Теорема. Для произвольного источника  и префиксного кода
и префиксного кода  избыточность кодирования неотрицательна, т. е.
избыточность кодирования неотрицательна, т. е. 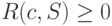 .
.
Доказательство.
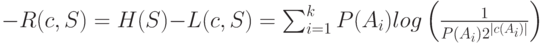
С учетом отмеченного выше неравенства для функции 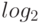 каждое слагаемое можно оценить сверху следующим образом:
каждое слагаемое можно оценить сверху следующим образом:

После суммирования получим
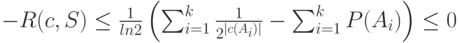
причем последнее неравенство следует из неравенства Крафта (6.3) для префиксного кода и равенства 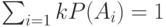 . Таким образом,
. Таким образом, 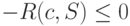 , что доказывает утверждение теоремы.
, что доказывает утверждение теоремы.
Из доказанной теоремы следует, что энтропия источника является нижней границей средней длины кодирования. Для источников, у которых вероятности являются целыми отрицательными степенями 2, эта граница достижима. Легко проверить, что для источника с распределением вероятностей 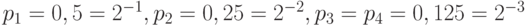 средняя длина кодирования равна 1,75 и совпадает с энтропией источника.
средняя длина кодирования равна 1,75 и совпадает с энтропией источника.
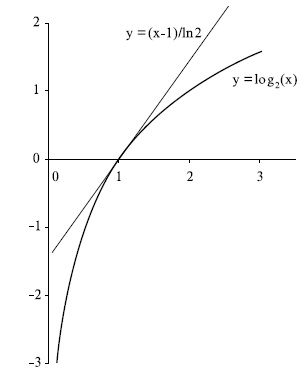
Для доказательства второй теоремы потребуется функция ![[x]](/sites/default/files/tex_cache/3e5314e9fd31509fdeb83faa0f729ba2.png) , которая называется "потолок" и определяется выражением
, которая называется "потолок" и определяется выражением ![[x]=min\{n|n \ge x, n - целое\}](/sites/default/files/tex_cache/6cae8324f017dfd1c9dabb41cecdb252.png) . Необходимые для доказательства свойства этой функции легко следуют из ее графика, показанного на рис.6.7, и заключаются в выполнении неравенств
. Необходимые для доказательства свойства этой функции легко следуют из ее графика, показанного на рис.6.7, и заключаются в выполнении неравенств ![0 \le [x]-x<1](/sites/default/files/tex_cache/013e5c57a26b20bdea1c517cc58ff517.png) .
.
Теорема. Для каждого источника  найдется префиксный код
найдется префиксный код  , избыточность которого не превышает единицы, т. е.
, избыточность которого не превышает единицы, т. е. 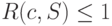 .
.
Пусть ![l_i=\left [log\frac{1}{P(A_i)} \right ]](/sites/default/files/tex_cache/fb76058d170d9bcefcea2bd7ac2ceee3.png) , где
, где ![[х]](/sites/default/files/tex_cache/21546749e77a701b446afdfa9c05922e.png) функция "потолок". Тогда
функция "потолок". Тогда
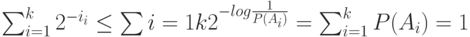
Это означает, что числа 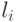 удовлетворяют неравенству Крафта. Тогда из теоремы Крафта следует, что найдется префиксное кодирование
удовлетворяют неравенству Крафта. Тогда из теоремы Крафта следует, что найдется префиксное кодирование  , такое что
, такое что 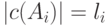 . Оценим избыточность этого кодирования
. Оценим избыточность этого кодирования
![R(c,S)=\sum_{i=1}^{k}P(A_i) \left (\left [log\frac{1}{P(A_i)}\right ]-log\frac{1}{P(A_i)} \right ) \le \sum_{i=1}^{k}P(A_i)=1](/sites/default/files/tex_cache/403bd709b6d7191c89d456db45be46c2.png)
Теорема доказана.
Данная теорема гарантирует, что для любого источника найдется префиксный код со средней длиной кодирования, превышающей энтропию не более чем на 1.

![График функции [x]](/EDI/27_01_19_1/1548541181-9080/tutorial/700/objects/6/files/06-07.jpg)