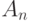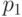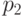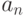Информационные технологии
Модели источников сообщений. Конечный вероятностный источник сообщений
Большинство информационных процессов связано не с отдельными сообщениями, а с последовательностями (потоками) сообщений. Например, при чтении человек анализирует последовательность букв, образующих слова и текст в целом; данные, поступающие от измерительных устройств или передающиеся по каналам связи, представляют собой последовательности сообщений. Для описания (моделирования) подобных ситуаций удобно ввести формальное понятие конечного (комбинаторного) источника сообщений.
Конечным (комбинаторным) источником называется произвольное множество  . Элементы множества
. Элементы множества  обычно называются сообщениями. Источник может породить любое из этих сообщений.
обычно называются сообщениями. Источник может породить любое из этих сообщений.
В некоторых случаях бывает известно, что в последовательностях сообщений одни сообщения встречаются чаще, чем другие. Например, в текстах на русском языке буквы "о", "е" встречаются более чем в 10 раз чаще букв "щ", "э", "ф" [30]. В других естественных языках наблюдается аналогичная ситуация. Использование дополнительной информации о частотах появления сообщений вероятностного источника может повысить эффективность обработки данных.
Формализацией понятия частоты появления того или иного события в математике является его вероятность. Вероятность события  обозначают обычно символом
обозначают обычно символом 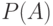 . Вероятность некоторого события (сообщения) можно представлять себе как долю тех случаев, в которых оно появляется, от общего числа появившихся событий (сообщений).
. Вероятность некоторого события (сообщения) можно представлять себе как долю тех случаев, в которых оно появляется, от общего числа появившихся событий (сообщений).
Так, если заданы четыре сообщения  с вероятностями
с вероятностями  , то это означает, что среди, например, 10000 переданных сообщений около 5000 раз появляется сообщение
, то это означает, что среди, например, 10000 переданных сообщений около 5000 раз появляется сообщение  , около 3750 - сообщение
, около 3750 - сообщение  и примерно по 625 раз - каждое из сообщений
и примерно по 625 раз - каждое из сообщений 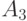 и
и 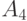 .
.
Распределение вероятностей появления отдельных сообщений в последовательности является важной ее характеристикой и существенно влияет на дальнейшие процессы обработки сообщений. Для дальнейшего удобно ввести формальное понятие конечного вероятностного источника сообщений.
Вероятностным источником  назовем произвольное множество (сообщений) с вероятностями (частотами) появления каждого из них. Удобно представлять вероятностный источник в виде таблицы.
назовем произвольное множество (сообщений) с вероятностями (частотами) появления каждого из них. Удобно представлять вероятностный источник в виде таблицы.
Вероятностный источник сообщений 
С позиций теории вероятностей вероятностный источник представляет собой дискретное распределение.
Характерной особенностью вероятностного источника является отсутствие полной определенности в поступлении очередного сообщения источника. Степень неопределенности для различных источников может значительно отличаться. Например, если рассматривать в качестве источника номера лотерейных билетов, крайне трудно определить номер оче-редного выигрышного билета. Однако если сообщениями источника считать исходы розыгрыша крупного выигрыша (автомобиля или квартиры) для конкретного билета, то сообщение такого источника предсказать не трудно. Скорее всего, на данный лотерейный билет крупного выигрыша не будет.
Для практики желательно уметь оценивать степень неопределенности различных вероятностных источников. Рассмотрим источник с  равновероятными сообщениями. Понятно, что степень неопределенности такого источника зависит от
равновероятными сообщениями. Понятно, что степень неопределенности такого источника зависит от  . При
. При 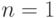 неопределенность отсутствует, т. к. может появиться только одно единственное сообщение. При больших
неопределенность отсутствует, т. к. может появиться только одно единственное сообщение. При больших  неопределенность больше (трудно предсказать появление какого-то определенного сообщения из
неопределенность больше (трудно предсказать появление какого-то определенного сообщения из  возможных). Из рассмотренного примера следует, что функция, описывающая неопределенность источника, должна принимать нулевое значение в случае отсутствия неопределенности (при
возможных). Из рассмотренного примера следует, что функция, описывающая неопределенность источника, должна принимать нулевое значение в случае отсутствия неопределенности (при 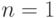 ), а при увеличении
), а при увеличении  она должна возрастать. Можно показать [31], что, наложив ряд простых и естественных требований на функцию, которая должна характеризовать неопределенность вероятностного источника, можно определить вид такой функции.
она должна возрастать. Можно показать [31], что, наложив ряд простых и естественных требований на функцию, которая должна характеризовать неопределенность вероятностного источника, можно определить вид такой функции.
Неопределенность вероятностного источника  с множеством сообщений
с множеством сообщений 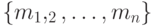 , вероятности появления которых равны
, вероятности появления которых равны 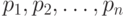 соответственно, принято описывать функцией (величиной)
соответственно, принято описывать функцией (величиной)
 |
( 6.1) |
Величина  называется энтропией источника сообщений
называется энтропией источника сообщений  . К. Шеннон предложил использовать энтропию для описания источников информации [30].
. К. Шеннон предложил использовать энтропию для описания источников информации [30].
Неопределенность источника можно трактовать как его информативность. Действительно, если неопределенность источника мала или даже равна 0, то очередное сообщение не несет новой информации, т. к. легко может быть предсказано заранее. И наоборот, очередное сообщение неопределенного источника плохо предсказуемо, скорей всего оно будет новым, отличным от любого ожидаемого сообщения.
Входящее в выражение (6.1) для энтропии выражение  можно рассматривать как информативность (неопределенность)
можно рассматривать как информативность (неопределенность)  -го сообщения источника, поскольку оно вполне соответствует интуитивному представлению о неопределенности. Энтропию можно рассматривать как среднюю информативность всего источника
-го сообщения источника, поскольку оно вполне соответствует интуитивному представлению о неопределенности. Энтропию можно рассматривать как среднюю информативность всего источника  .
.
От вероятностного источника зависит выбор оптимального в среднем способа кодирования сообщений.
Кодирование сообщений источника и текстов. Равномерное кодирование. Дерево кода
Чаще всего информация представляется в виде языковых сообщений (цепочек знаков или слов), причем в процессе ее обработки форма представления может меняться. Например, сообщение, предназначенное для передачи по телеграфу, первоначально может быть представлено в виде рукописного текста. Телеграфист переводит это сообщение в последовательность длинных, коротких импульсов и пауз, передающихся по телеграфному каналу. А на приемном конце такая последовательность может быть преобразована в печатный текст. Рассмотренные преобразования представляют собой пример кодирования сообщений. Еще одним примером кодирования является тайнопись, когда исходное сообщение преобразуется в другую форму, скрывающую содержание исходного сообщения.
Различные задачи кодирования можно формализовать следующим образом. Пусть  и
и  алфавиты,
алфавиты,  некоторое множество слов в алфавите
некоторое множество слов в алфавите  . Тогда функция
. Тогда функция
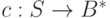
называется кодированием или кодом. Кодом называется также образ отображения  , обозначаемый
, обозначаемый  . Если существует обратная функция
. Если существует обратная функция  , то она называется декодированием. Одно и то же множество сообщений можно закодировать многими различными способами. Поэтому среди многих вариантов кодирования ищут такой, который был бы оптимальным в некотором смысле или обладал определенными полезными свойствами. Наиболее естественным требованием является возможность декодирования.
, то она называется декодированием. Одно и то же множество сообщений можно закодировать многими различными способами. Поэтому среди многих вариантов кодирования ищут такой, который был бы оптимальным в некотором смысле или обладал определенными полезными свойствами. Наиболее естественным требованием является возможность декодирования.
Побуквенное (алфавитное) кодирование. Обычно, кодирование множества слов  производится с помощью функции кодирующей отдельные буквы алфавита
производится с помощью функции кодирующей отдельные буквы алфавита  . Для этого случая определение кода будет следующим.
. Для этого случая определение кода будет следующим.
Кодом называется отображение
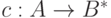 |
( 6.2) |
сопоставляющее каждому знаку из алфавита  некоторое слово, которое составлено из знаков, входящих в
некоторое слово, которое составлено из знаков, входящих в  . Слова, входящие в
. Слова, входящие в  , называются кодовыми словами. Отображение (6.2) может задаваться любым из известных в математике способов. Для конечного множества
, называются кодовыми словами. Отображение (6.2) может задаваться любым из известных в математике способов. Для конечного множества  чаще всего используется табличный способ, задающий код (6.2) таблицей.
чаще всего используется табличный способ, задающий код (6.2) таблицей.
Такая таблица называется кодовой таблицей. В качестве примера можно привести таблицу кодирования алфавита 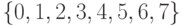 из цифр восьмеричной системы счисления словами из упоминавшегося ранее бинарного алфавита
из цифр восьмеричной системы счисления словами из упоминавшегося ранее бинарного алфавита  . В данном случае отображение (6.2) имеет вид
. В данном случае отображение (6.2) имеет вид  .
.
Еще одним примером является так называемый код ASCII, фрагмент которого показан в следующей таблице.
| Знак | Кодовое слово (в десятичной системе счисления) | Кодовое слово (в шестнадцатеричной системе счисления) |
|---|---|---|
| … | … | |
| a | 97 | 61 |
| b | 98 | 62 |
| c | 99 | 63 |
| d | 100 | 64 |
| e | 101 | 65 |
| f | 102 | 66 |
| g | 103 | 67 |
| h | 104 | 68 |
| i | 105 | 69 |
| j | 106 | 6A |
| … | … |
Кодирование слов. Отображение (6.2) позволяет перейти от кодирования отдельных знаков (букв конечного алфавита) к кодированию слов. Если 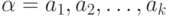 - слово, состоящее из знаков (полученное конкатенацией знаков)
- слово, состоящее из знаков (полученное конкатенацией знаков)  , то кодом
, то кодом  слова
слова  (по определению) является конкатенация кодов
(по определению) является конкатенация кодов  знаков
знаков  , образующих слово, т. е.
, образующих слово, т. е.  . Например, с применением таблицы ASCII кода (см. последнюю таблицу) слово head будет закодировано последовательностью 10410197100 при использовании десятичной системы счисления или последовательностью 68656164 - в шестнадцатеричной.
. Например, с применением таблицы ASCII кода (см. последнюю таблицу) слово head будет закодировано последовательностью 10410197100 при использовании десятичной системы счисления или последовательностью 68656164 - в шестнадцатеричной.
Условие (необходимое) однозначной декодируемости заключается в инъективности отображения (6.2). Инъективность обеспечивает однозначную декодируемость отдельных знаков из алфавита  . Однако однозначной декодируемости слов из
. Однако однозначной декодируемости слов из  это условие не обеспечивает, если коды отдельных знаков, входящих в слово, следуют один за другим и не разделяются специальным символом. Подробнее проблема однозначной декодируемости будет рассмотрена позже.
это условие не обеспечивает, если коды отдельных знаков, входящих в слово, следуют один за другим и не разделяются специальным символом. Подробнее проблема однозначной декодируемости будет рассмотрена позже.
В частном случае, когда знаки из  кодируются однобуквенными словами, отображение (6.2) имеет вид
кодируются однобуквенными словами, отображение (6.2) имеет вид  и представляет собой простую замену (подстановку) знаков. Однако чаще всего, в основном из-за использования в большинстве технических устройств обработки информации двоичного алфавита
и представляет собой простую замену (подстановку) знаков. Однако чаще всего, в основном из-за использования в большинстве технических устройств обработки информации двоичного алфавита  , каждый знак из
, каждый знак из  кодируется последовательностью знаков (словом) из B.
кодируется последовательностью знаков (словом) из B.
Недостаточность количества знаков в алфавите  является препятствием применения простой замены для кодирования (не обеспечивается инъективность и, следовательно, однозначность декодируемости при
является препятствием применения простой замены для кодирования (не обеспечивается инъективность и, следовательно, однозначность декодируемости при  ). Для устранения этой проблемы используются множества новых, "составных" объектов из степеней
). Для устранения этой проблемы используются множества новых, "составных" объектов из степеней  алфавита
алфавита  . Множество
. Множество  состоит из упорядоченных последовательностей элементов из
состоит из упорядоченных последовательностей элементов из  (векторов) длины
(векторов) длины  . Число элементов
. Число элементов 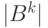 множества
множества  равно
равно 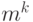 . Например, для двоичного алфавита
. Например, для двоичного алфавита  имеем
имеем  . Таким образом, взяв достаточно большую степень
. Таким образом, взяв достаточно большую степень  , можно получить нужное количество элементов вторичного алфавита.
, можно получить нужное количество элементов вторичного алфавита.
Если каждый знак алфавита  отображается при кодировании
отображается при кодировании  в слово одинаковой длины
в слово одинаковой длины  , то говорят, что код является кодом постоянной длины. Такие коды широко распространены, поскольку для обработки сообщений используются вычислительные машины, коммуникацион-ные устройства и другое оборудование, имеющее регистры фиксированного размера.
, то говорят, что код является кодом постоянной длины. Такие коды широко распространены, поскольку для обработки сообщений используются вычислительные машины, коммуникацион-ные устройства и другое оборудование, имеющее регистры фиксированного размера.
Процедуру кодирования слова  в алфавите
в алфавите  можно представить следующим образом. Имеется кодовая таблица, в левом столбце которой находятся кодируемые буквы алфавита
можно представить следующим образом. Имеется кодовая таблица, в левом столбце которой находятся кодируемые буквы алфавита  , а в правом столбце - соответствующие кодовые слова (кодовые слова могут иметь различную длину).
, а в правом столбце - соответствующие кодовые слова (кодовые слова могут иметь различную длину).
Для каждого знака слова  , начиная с первого знака, в кодовой таблице находится строка, в которой в левом поле располагается кодируемый знак (буква), и из правого поля этой строки берется соответствующее кодовое слово в алфавите
, начиная с первого знака, в кодовой таблице находится строка, в которой в левом поле располагается кодируемый знак (буква), и из правого поля этой строки берется соответствующее кодовое слово в алфавите  . Найденное кодовое слово приписывается слева (конкатенируется) к уже сформированной части кода слова
. Найденное кодовое слово приписывается слева (конкатенируется) к уже сформированной части кода слова  . Кодовое слово первой буквы слова
. Кодовое слово первой буквы слова  приписывается к пустому слову е. Эта процедура схематически показана на рис.6.4.
приписывается к пустому слову е. Эта процедура схематически показана на рис.6.4.