Информационные технологии
Основные понятия теории формальных языков
Формальные языки являются упрощенными моделями реально существующих естественных и искусственных языков. Как и реальные языки, формальный язык состоит из множества слов, составленных из букв. Прежде чем дать точное определение формального языка, рассмотрим некоторые вспомогательные понятия.
Алфавитом называется конечное непустое множество знаков. Обычно подразумевается, что это множество линейно упорядочено. Условимся обозначать алфавиты символом  . Наиболее часто используются следующие алфавиты.
. Наиболее часто используются следующие алфавиты.
-
 - бинарный, или двоичный, алфавит, состоящий из двух знаков: 0 и 1.
- бинарный, или двоичный, алфавит, состоящий из двух знаков: 0 и 1. -
 - множество строчных букв английского алфавита.
- множество строчных букв английского алфавита. - Множество ASCII-символов или множество всех печатных ASCII-символов.
- Множество десятичных цифр
 является алфавитом, с помощью которого записываются неотрицательные целые числа.
является алфавитом, с помощью которого записываются неотрицательные целые числа. - Алфавит
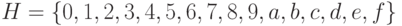 также служит для записи неотрицательных целых чисел в шестнадцатеричной системе счисления.
также служит для записи неотрицательных целых чисел в шестнадцатеричной системе счисления. - Алфавит
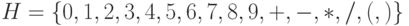 позволяет записывать арифметические выражения над целыми числами.
позволяет записывать арифметические выражения над целыми числами.
Следует отметить, что алфавит  содержит 10 десятичных цифр т. е.
содержит 10 десятичных цифр т. е.  .
.
Слово или цепочка - это конечная последовательность знаков некоторого алфавита. Например, 01101 - это цепочка в бинарном алфавите  . Цепочки 15903 и 15df10 являются цепочками в алфавите
. Цепочки 15903 и 15df10 являются цепочками в алфавите  и
и  соответственно.
соответственно.
Пустая цепочка - это цепочка, не содержащая ни одного символа. Эту цепочку, обозначаемую е, можно рассматривать как цепочку в любом алфавите.
Часто бывает необходимо или удобно классифицировать слова по их длине, т.е. по числу позиций, которые занимают знаки в слове. Например, слово 01101 имеет длину 5. Обычно говорят, что длина цепочки - это число знаков в ней. Это определение широко распространено, но не вполне корректно. Так, в цепочке 01101 всего 2 символа, но число позиций в ней - пять, поэтому она имеет длину 5. Все же следует иметь в виду, что часто пишут "число знаков", подразумевая "число позиций".
Длину некоторой цепочки  обычно обозначают
обычно обозначают 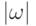 . Например,
. Например, 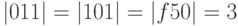 , а
, а  .
.
Степени алфавита. Для множества всех цепочек определенной длины, состоящих из символов некоторого алфавита , удобно использовать, по аналогии с декартовыми степенями множеств, знак степени. Обозначим через 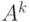 множество всех слов длины
множество всех слов длины  , состоящих из знаков алфавита
, состоящих из знаков алфавита  . Данное множество с точностью до обозначений его элементов совпадает с декартовым произведением
. Данное множество с точностью до обозначений его элементов совпадает с декартовым произведением  . Различие заключается в том, что элементы декартового произведения обычно заключаются в скобки, а слова из
. Различие заключается в том, что элементы декартового произведения обычно заключаются в скобки, а слова из 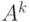 записываются без скобок.
записываются без скобок.
Рассмотрим примеры такой записи 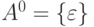 независимо от алфавита
независимо от алфавита  , т.е.
, т.е.  - единственное слово длины 0. Для
- единственное слово длины 0. Для  и так далее. Отметим, что между
и так далее. Отметим, что между  и
и 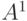 есть небольшое различие. Дело в том, что
есть небольшое различие. Дело в том, что  есть алфавит, и его элементы 0 и 1 являются символами, а
есть алфавит, и его элементы 0 и 1 являются символами, а 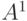 является множеством слов, и его элементы - это слова 1 и 0, каждое длиной 1. Мы не будем вводить разные обозначения для этих множеств, полагая, что из контекста будет понятно, является {0,1} или подобное ему множество алфавитом или же множеством цепочек.
является множеством слов, и его элементы - это слова 1 и 0, каждое длиной 1. Мы не будем вводить разные обозначения для этих множеств, полагая, что из контекста будет понятно, является {0,1} или подобное ему множество алфавитом или же множеством цепочек.
Множество всех слов над алфавитом  принято обозначать
принято обозначать  . Так, например
. Так, например  . По-другому это множество можно записать в виде
. По-другому это множество можно записать в виде 
Множество всех непустых слов в алфавите  обозначают через
обозначают через 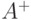 . Таким образом, имеют место следующие равенства:
. Таким образом, имеют место следующие равенства:

Конкатенация слов. Пусть  и
и  - слова. Тогда
- слова. Тогда  обозначает их конкатенацию (соединение), т.е. слово, в котором последовательно записаны слова
обозначает их конкатенацию (соединение), т.е. слово, в котором последовательно записаны слова  и
и  . Более строго, если
. Более строго, если  - слово из
- слово из  символов:
символов: 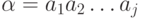 , а
, а  - слово из
- слово из  символов
символов 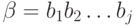 , то
, то 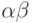 - это слово длины
- это слово длины  ,
, 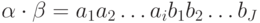 .
.
Конкатенацию можно рассматривать как алгебраическую операцию на множестве всех слов в алфавите  , которая любым словам
, которая любым словам  и
и  из
из  сопоставляет слово из
сопоставляет слово из  . Эта операция обладает некоторыми привычными свойствами алгебраических операций. Так, конкатенация является ассоциативной операцией, то есть для любых слов
. Эта операция обладает некоторыми привычными свойствами алгебраических операций. Так, конкатенация является ассоциативной операцией, то есть для любых слов 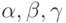 справедливо равенство
справедливо равенство  . Скобки в этом выражении определяют порядок выполнения операций конкатенации. Доказательство ассоциативности следует непосредственно из определения операции конкатенации. Операция конкатенации не является перестановочной (коммутативной), что следует из следующего примера.
. Скобки в этом выражении определяют порядок выполнения операций конкатенации. Доказательство ассоциативности следует непосредственно из определения операции конкатенации. Операция конкатенации не является перестановочной (коммутативной), что следует из следующего примера.
Пусть 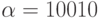 и
и  . Тогда
. Тогда 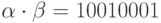 , а
, а 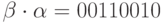 и, следовательно,
и, следовательно, 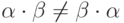 .
.
Для пустого слова  и любого слова
и любого слова  справедливы равенства
справедливы равенства  . Таким образом,
. Таким образом,  является единицей (нейтральным элементом) относительно операции конкатенации, поскольку результат ее конкатенации с любым словом дает то же самое слово (аналогично тому, как 0, нейтральный элемент относительно сложения, при сложении с любым числом
является единицей (нейтральным элементом) относительно операции конкатенации, поскольку результат ее конкатенации с любым словом дает то же самое слово (аналогично тому, как 0, нейтральный элемент относительно сложения, при сложении с любым числом  дает число
дает число  ). Описанные выше свойства операции конкатенации означают, что множество всех слов
). Описанные выше свойства операции конкатенации означают, что множество всех слов  является (свободным) моноидом относительно операции конкатенации [29].
является (свободным) моноидом относительно операции конкатенации [29].
Если 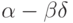 , то
, то  называется началом, или префиксом, слова
называется началом, или префиксом, слова  , а
, а  - окончанием, или постфиксом, слова
- окончанием, или постфиксом, слова  .
.
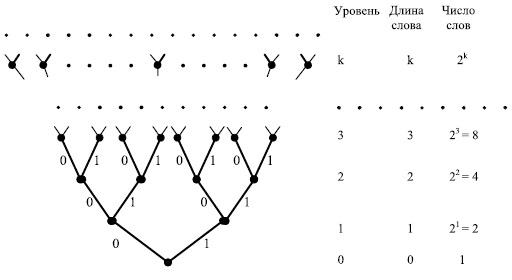
Множество всех слов можно представить графически в виде помеченного корневого дерева (дерева с выделенной вершиной, называемой корнем). Вершинам дерева соответствуют слова в алфавите  . Поэтому это дерево можно назвать словарным деревом, а поскольку все слова представлены в этом дереве, то его также можно назвать словарным универсумом. Это дерево имеет ярусное строение. На одном ярусе располагаются все слова одинаковой длины.
. Поэтому это дерево можно назвать словарным деревом, а поскольку все слова представлены в этом дереве, то его также можно назвать словарным универсумом. Это дерево имеет ярусное строение. На одном ярусе располагаются все слова одинаковой длины.
На рис.6.3 изображен фрагмент словарного универсума для случая, когда алфавит состоит из двух знаков, то есть  .
.
Опишем процедуру построения словарного дерева. Построение начинается с вершины, которая является корнем дерева и которая соответствует пустому слову  . Эта (единственная) вершина образует нулевой ярус (уровень) дерева. Первый ярус дерева состоит из
. Эта (единственная) вершина образует нулевой ярус (уровень) дерева. Первый ярус дерева состоит из  вершин (
вершин ( - число букв в алфавите
- число букв в алфавите  ), которые соединены с корнем ребрами, помеченными буквами алфавита
), которые соединены с корнем ребрами, помеченными буквами алфавита  . Вершины первого уровня соответствуют всем однобуквенным словам, которые получаются конкатенацией букв, помечающих ребра, с пустым словом.
. Вершины первого уровня соответствуют всем однобуквенным словам, которые получаются конкатенацией букв, помечающих ребра, с пустым словом.
Дальнейшее построение дерева выполняется аналогичным образом. Если  -й уровень дерева сформирован, то есть в дереве уже имеется
-й уровень дерева сформирован, то есть в дереве уже имеется 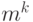 вершин, соответствующих всем словам длины
вершин, соответствующих всем словам длины  , к каждой вершине
, к каждой вершине  -го уровня присоединяется
-го уровня присоединяется  вершин
вершин 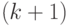 -го уровня посредством ребер, помеченных буквами алфавита
-го уровня посредством ребер, помеченных буквами алфавита  . Любой вершине
. Любой вершине 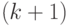 -го уровня соответствует слово, которое получается конкатенацией некоторого
-го уровня соответствует слово, которое получается конкатенацией некоторого  -буквенного слова и буквы, помечающей ребро между этими словами.
-буквенного слова и буквы, помечающей ребро между этими словами.
Таким образом, из процедуры построения дерева следует, что ребром в дереве соединяются только те вершины, которым соответствуют слова, отличающиеся по длине на 1. При этом более длинное слово является конкатенацией более короткого слова и буквы, помечающей ребро. Ясно также, что любое слово  , соответствующее вершине, которая лежит на пути из корня дерева к вершине, соответствующей слову
, соответствующее вершине, которая лежит на пути из корня дерева к вершине, соответствующей слову  , является пре-фиксом слова
, является пре-фиксом слова  , то есть
, то есть  ,
, 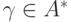 .
.
Рассмотренные выше понятия и примеры позволяют сформулировать точное определение формального языка. Пусть  - некоторый фиксированный алфавит. Множество слов, каждое из которых принадлежит
- некоторый фиксированный алфавит. Множество слов, каждое из которых принадлежит  , называют формальным языком. Иными словами, если
, называют формальным языком. Иными словами, если  - алфавит и
- алфавит и  , то
, то  - это язык над
- это язык над  или в
или в  . Отметим, что язык в
. Отметим, что язык в  не обязательно должен содержать цепочки, в которые входят все символы
не обязательно должен содержать цепочки, в которые входят все символы  . Поэтому если известно, что
. Поэтому если известно, что  является языком в
является языком в  , то можно утверждать, что
, то можно утверждать, что  - это язык над любым алфавитом, содержащим
- это язык над любым алфавитом, содержащим  .
.
Однако оправданием использования термина "язык" для множества  может служить то, что и обычные языки можно рассматривать как множества цепочек (слов). Возьмем в качестве примера русский язык, где набор всех литературных русских слов есть множество цепочек в алфавите (русских же букв). Еще один пример - язык программирования
может служить то, что и обычные языки можно рассматривать как множества цепочек (слов). Возьмем в качестве примера русский язык, где набор всех литературных русских слов есть множество цепочек в алфавите (русских же букв). Еще один пример - язык программирования  или любой другой язык программирования, в котором правильно написанные программы представляют собой подмножество множества всех возможных цепочек, а цепочки состоят из символов алфавита данного языка. Этот алфавит является подмножеством символов ASCII. Алфавиты для разных языков программирования могут быть различными, хотя обычно они состоят из прописных и строчных букв, цифр, знаков пунктуации и математических символов.
или любой другой язык программирования, в котором правильно написанные программы представляют собой подмножество множества всех возможных цепочек, а цепочки состоят из символов алфавита данного языка. Этот алфавит является подмножеством символов ASCII. Алфавиты для разных языков программирования могут быть различными, хотя обычно они состоят из прописных и строчных букв, цифр, знаков пунктуации и математических символов.
Существует, однако, множество других языков. Приведем несколько примеров.
Язык, состоящий из всех цепочек, в которых  единиц следуют за
единиц следуют за  нулями для некоторого
нулями для некоторого 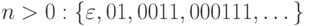 .
.
Множество цепочек, состоящих из 0 и 1 и содержащих поровну тех и других: 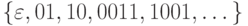 .
.
Множество двоичных записей простых чисел:  .
.
Множество 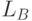 всех правильных скобочных выражений,
всех правильных скобочных выражений,  .
.
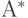 - язык для любого алфавита
- язык для любого алфавита  .
.
 - пустой язык в любом алфавите.
- пустой язык в любом алфавите.
\{\varepsilon\} - язык, содержащий одну лишь пустую цепочку. Он также является языком в любом алфавите. Заметим, что  ; первый не содержит вообще никаких цепочек, а второй состоит из одной цепочки.
; первый не содержит вообще никаких цепочек, а второй состоит из одной цепочки.
Единственное существенное ограничение для множеств, которые могут быть языками, состоит в том, что все алфавиты конечны.
Некоторые из приведенных выше языков содержат конечное число слов. В этом случае язык, в принципе, может быть задан перечислением входящих в него слов.
Однако некоторые языки и могут содержать бесконечное число цепочек, но эти цепочки должны быть составлены из символов некоторого фиксированного конечного алфавита. В общем случае язык - это бесконечное множество слов. В этом заключается сложность работы с языками, в частности, их задание или описание. Несмотря на то, что язык содержит бесконечное число слов, желательно, чтобы описание такого языка было конечным. Один из подходов заключается в том, что применяется процедура (называемая грамматикой) построения слов точно определенным способом с применением правил грамматики. Другой подход использует алгоритм, который для каждого слова однозначно определяет, принадлежит ли оно языку или нет.