Особенности представления чисел в ЭВМ

Арифметические и побитовые операторы языка Java

К арифметическим операторам языка Java, которые определены для всех числовых типов, относятся: + (сложение и унарный плюс), += (сложение с присваиванием), - (вычитание и унарный минус), -= (вычитание с присваиванием), * (умножение), *= (умножение с присваиванием), / (деление), /= (деление с присваиванием), % (остаток от деления или деление по модулю), %= (остаток от деления с присваиванием), ++ (инкремент) и -- (декремент).

Любой оператор с присваиванием с точки зрения получаемого результата эквивалентен выполнению соответствующей операции с последующим присваиванием, но работает обычно быстрее: a @= b эквивалентно а = a @ b (здесь символ @ означает любую из бинарных арифметических операций).

Результат выполнения операций деления и деления по модулю (нахождения остатка) для целочисленных операндов является целым числом. Так, например, 5/3 равняется 1.

Наконец, операции инкремента и декремента соответственно увеличивают и уменьшают свой операнд на единицу. Они бывают префиксными и тогда изменение их операнда происходит до того, как выполняются другие действия в выражении, и постфиксными, когда изменение происходит после вычисления выражения:

int i = 2, j = 3;   // i = 2, j = 3
    int k = i + j++;    // k = 5, j = 4
    int m = --i;        // i = 1, m = 1

С величинами целых типов можно выполнять дополнительные действия. К побитовым (или поразрядным) операторам языка Java относятся следующие: ~ (дополнение), & (побитовое И ), &= (побитовое И с присваиванием), | (побитовое Или ), |= (побитовое Или с присваиванием), ^ (исключающее Или ), ^= (исключающее Или с присваиванием), << (сдвиг влево), <<= (сдвиг влево с присваиванием), >> (сдвиг вправо), >>= (сдвиг вправо с присваиванием), >>> (сдвиг вправо с размножением нуля) и >>>= (сдвиг вправо с присваиванием с размножением нуля).

Результаты операций побитового дополнения, Или, исключающего Или и И получаются путем выполнения над каждым из битов операнда (операндов) действий в соответствии с таблицей 4.1.

Например, 4^5 равняется 1 (ибо двоичные представления этих чисел есть соответственно 100 и 101 ).

У операторов сдвига второй аргумент показывает количество разрядов, на которое надо осуществить сдвиг в двоичном представлении первого операнда влево (для << ) или вправо (для >> и >>> ).

int i = 3, j = 100;	// i = 3, j = 100
    int k = i << 4;     // k = 48
    int m = j >> 2;     // m = 25

Легко понять, что сдвиг влево на разрядов эквивалентен умножению на , а сдвиг вправо — делению на то же число.

Задачи для самостоятельного решения

Задача 4.3.Предъявите целое число такое, что .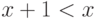

Задача 4.4.Явно перечислите и изобразите на числовой прямой все точки множества , сделав следующие допущения: числа хранятся в нормализованной форме с плавающей точкой; для хранения как мантиссы, так и порядка числа отводится по три бита (из которых в обоих случаях один является знаковым); никаких особых значений нет.

Задача 4.5.Предъявите действительное (типа double ) число такое, что 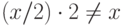. Воспользуйтесь тем, что класс java.lang.Double определяет константу MIN_VALUE.

Задача 4.6.Определите (приближенно) 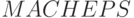(машинное эпсилон) для типов double и float. Машинным эпсилоном называется наибольшее число данного типа, удовлетворяющее соотношению .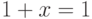

Задача 4.7.Предъявите последовательность чисел (типа float ), при суммировании которой в прямом и обратном порядке результаты будут отличаться не менее, чем вдвое.

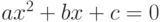Задача 4.8.Напишите программу, вводящую действительные коэффициенты , и квадратного уравнения с положительным дискриминантом, находящую оба корня этого уравнения достаточно точно во всех случаях.

Числа произвольной длины и точности

При необходимости на любом алгоритмическом языке можно реализовать так называемую длинную арифметику, позволяющую работать с целыми числами произвольной длины. При этом числа размещаются в совокупности последовательных байтов необходимой длины. Естественно, что эффективность любых операций над такими числами значительно ниже, чем над величинами типа int.

В случае языка Java пакет java.math дает возможность программисту работать с целыми и вещественными числами произвольной длины и точности, не требуя при этом никакого дополнительного кодирования, однако обсуждение данного пакета в нашем курсе не предполагается.

Некоторые задачи, требующие реализовать арифметические операции над целыми числами достаточно большой величины, будут рассмотрены в курсе далее, а вот проблемы, связанные с особенностями представления действительных чисел, нас интересовать не будут. О них придется вспомнить позже, при изучении курса вычислительной математики.