| Что такое сеть? |
Сетевое планирование и управление
Для нумерации событий применяется следующий способ. Вычеркиваются все
работы, выходящие из события с номером "0", и просматриваются все
события, в которых оканчиваются эти вычеркнутые работы. Среди
просмотренных находятся события, которые не имеют входящих в них работ (за
исключением уже вычеркнутых). Они называются событиями первого
ранга и обозначаются (вообще, в произвольном порядке) числами
натурального ряда, начиная с единицы (на рис. 14.1 это событие 1). Затем
вычеркиваются все работы, выходящие из событий первого ранга, и среди них
находятся события, не имеющие входящих работ (кроме вычеркнутых). Это —
события второго ранга, которые нумеруются следующими числами натурального
ряда (например, 2 и 3 на рис. 14.1). Проделав таким способом  шаг, определяют события
шаг, определяют события  - го ранга, и просматривая
события, в которых эти работы заканчиваются, выбирают события, не имеющие
ни одной входящей в них работы (кроме вычеркнутых). Это события
- го ранга, и просматривая
события, в которых эти работы заканчиваются, выбирают события, не имеющие
ни одной входящей в них работы (кроме вычеркнутых). Это события  -го
ранга, и нумеруются они последовательными числами натурального ряда,
начиная с наименьшего, еще не использованного числа при предыдущей
нумерации на
-го
ранга, и нумеруются они последовательными числами натурального ряда,
начиная с наименьшего, еще не использованного числа при предыдущей
нумерации на  -м шаге.
-м шаге.
Сетевой график содержит конечное число событий. Поскольку в процессе вычеркивания движение осуществляется в направлении стрелок (работ), никакое предшествующее событие не может получить номер, больший, чем любое последующее. Всегда найдется хотя бы одно событие соответствующего ранга, и все события получат номера за конечное число шагов.
Работа обычно кодируется номерами событий, между которыми они заключены,
то есть парой  , где
, где  — номер
предшествующего события,
— номер
предшествующего события,  —
номер последующего события.
—
номер последующего события.
В одно и то же событие могут входить (выходить) одна или несколько работ. Поэтому свершение события зависит от завершения самой длительной из всех входящих в него работ.
Взаимосвязь между работами определяется тем, что начало последующей работы обусловлено окончанием предыдущей. Отсюда следует, что нет работ, не связанных началом и окончанием с другими работами через события.
Последовательные работы и события формируют цепочки (пути), которые ведут
от исходного события сетевого графика к завершающему. Например, путь  сетевого графика, показанного на
(рис.14.1), включает в себя события
сетевого графика, показанного на
(рис.14.1), включает в себя события  и работы
и работы  .
.
На основании изложенного можно сказать, что ранг события — это
максимальное число отдельных работ, входящих в какой-либо из путей,
ведущих из нулевого (исходного) события в данное. Так, события первого
ранга не имеют путей, состоящих более чем из одной работы, ведущих в них
из 0 (например, событие 1 на рис.14.1). События второго ранга связаны с 0
путями, которые состоят не более чем из двух работ, причем для каждого
события второго ранга хоть один такой путь обязательно существует.
Например, на (рис.14.1) событие 4 — событие третьего ранга, так как пути,
ведущие в это событие из 0, включают только три работы —  и
и  или
или 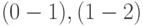 и
и 
Построенный таким образом сетевой график в терминах теории графов представляет собой направленный граф.
На рисунке изображен сетевой график. Граф, не содержащий циклов и имеющий только один исток и только один сток, называется направленным графом. Сетевой график есть ориентированный связный асимметрический граф с одним истоком, одним стоком и без циклов, то есть это направленный граф. При этом вершинами графа служат события сетевого графика, а дугами (ребрами) — работы сетевого графика.
Продолжительность работы представляет собой, в терминах теории графов,
длину дуги. Следовательно, длина пути  — это сумма длин
всех дуг, образующих данный путь, то есть
— это сумма длин
всех дуг, образующих данный путь, то есть  , где
символом
, где
символом  обозначается дуга, которая соединяет вершины
обозначается дуга, которая соединяет вершины  и
и  и направлена от вершины
и направлена от вершины  к
вершине
к
вершине  .
.


