| Что такое сеть? |
Сетевое планирование и управление
Определение критического пути
Полный путь, суммарная продолжительность работ на котором является максимальной, называется критическим, то есть это самый длинный по времени путь в сетевом графике от исходного события до завершающего. Продолжительность критического пути определяет минимальное время, объективно необходимое для выполнения всего комплекса мероприятий, входящих в планируемый процесс. За время, меньше времени критического пути, весь комплекс мероприятий совершиться не может. Поэтому любая задержка на работах критического пути увеличивает время выполнения всего процесса.
События, через которые проходит критический путь, называются критическими. Работы, входящие в состав критического пути, называются критическими.
Задержка в выполнении работы на величину  приводит к задержке в наступлении завершающего события на величину
приводит к задержке в наступлении завершающего события на величину 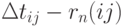 .
.
Задержка в выполнении работы на величину  вообще не повлияет ни на один другой срок, определенный данным сетевым
графиком. Следовательно, у критических работ и полные, и свободные резервы
времени равны нулю. Вообще говоря, равенство нулю полного резервного
времени работы является необходимым и достаточным признаком того, что
данная работа критическая. Напротив, свободный резерв времени может быть
равным нулю и у некритических работ.
вообще не повлияет ни на один другой срок, определенный данным сетевым
графиком. Следовательно, у критических работ и полные, и свободные резервы
времени равны нулю. Вообще говоря, равенство нулю полного резервного
времени работы является необходимым и достаточным признаком того, что
данная работа критическая. Напротив, свободный резерв времени может быть
равным нулю и у некритических работ.
Таким образом, критический путь находится посредством определения работ, полные резервы времени которых равны нулю.
Определение полного резерва времени ненапряженного пути
События и работы, лежащие не на критических путях (такие пути называются ненапряженными ), обладают резервами времени. Выявление этих резервов наравне с определением критического пути составляет основное содержание анализа сетевой модели. С работ и путей, имеющих резервы времени, можно снять ресурсы и направить их на выполнение работ, лежащих на критических путях. Этим самым можно добиться сокращения сроков проведения критических работ, а следовательно, и всей операции в целом, используя только внутренние резервы.
Полным резервом времени ненапряженного пути называется разница между его длиной и длиной критического пути. Полный резерв времени ненапряженного пути показывает, на сколько в сумме может быть увеличена продолжительность всех работ этого пути без изменения срока выполнения всего процесса в целом. Однако при этом ненапряженный и критический пути не должны пересекаться. Если они пересекаются, то полный резерв времени определяется самым длительным участком напряженного пути, заключенным между соответствующими парами событий критического пути.
Формирование временных оценок работ
Адекватность сетевой модели отображаемому реальному процессу и, соответственно, оперативность руководства процессом во многом зависят от правильности временных оценок выполняемых работ. Если, например, продолжительность работ будет занижена, то это вызовет поспешность в подготовке всей операции в целом, что, в свою очередь, может привести к срыву и цель не будет достигнута. А завышение сроков выполнения отдельных работ может привести к потере времени, что также, как правило, ведет к срыву.
Для определения временных и других характеристик, необходимых для оценки длительности работ или расхода ресурсов, могут использоваться статистические данные, полученные опытным путем. Такие оценки однозначно определяются из нормативов. Если такие нормативы отсутствуют, то разработчиками сетевого графика даются три оценки времени:
- оптимистическая (
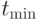 );
); - пессимистическая (
 );
); - наиболее вероятная (
 ).
).
Оптимистическая оценка — продолжительность работы в наиболее благоприятных условиях.
Пессимистическая оценка — продолжительность работы при самом неблагоприятном стечении обстоятельств.
Наиболее вероятная оценка — продолжительность работы при условии, что не возникнет никаких неожиданных трудностей.
На основании этих оценок вычисляются оценки 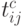 и их
дисперсии
и их
дисперсии 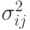 по следующим эмпирическим формулам:
по следующим эмпирическим формулам:
 |
( 14.6) |
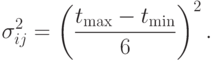 |
( 14.7) |
В этом случае все расчеты проводятся так, как было рассмотрено выше. Затем
рассчитываются вероятности того, что полученные параметры сетевой модели
(ранние сроки, поздние сроки, резервы и т.д.) действительно будут
находиться в тех или иных числовых границах. При этом вводится допущение,
что продолжительности двух любых работ являются независимыми величинами,
а величина 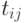 определенная формулой (14.6), принимается
равной математическому ожиданию продолжительности данной работы (
определенная формулой (14.6), принимается
равной математическому ожиданию продолжительности данной работы ( 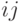 ).
Тогда математическое ожидание любого параметра сетевой модели, являющегося
суммой величин вида
).
Тогда математическое ожидание любого параметра сетевой модели, являющегося
суммой величин вида 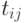 , есть сумма математических ожиданий
слагаемых, то есть
, есть сумма математических ожиданий
слагаемых, то есть 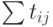 . Точнее, это оценка снизу, так как
все параметры сетевой модели носят, так сказать, экстремальный характер.
Соответственно, дисперсия параметра будет
. Точнее, это оценка снизу, так как
все параметры сетевой модели носят, так сказать, экстремальный характер.
Соответственно, дисперсия параметра будет 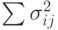 .
Если считать, что время выполнения работ подчиняется нормальному закону,
вероятность совершения
.
Если считать, что время выполнения работ подчиняется нормальному закону,
вероятность совершения  -го события в расчетный срок можно
определить по следующей формуле:
-го события в расчетный срок можно
определить по следующей формуле:
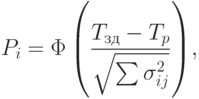 |
( 14.8) |
где  — функция Лапласа;
— функция Лапласа; 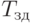 — директивный срок;
— директивный срок;  — время раннего свершения
— время раннего свершения  -го события;
-го события; 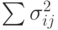 — сумма дисперсий работ, которые
использовались при вычислении раннего срока наступления
— сумма дисперсий работ, которые
использовались при вычислении раннего срока наступления  -го события.
-го события.

