| Что такое сеть? |
Орграфы
Определения
Сначала напомним некоторые определения из "Основные понятия теории графов" .
Орграфом  называется
пара
называется
пара  , где
, где  непустое
конечное множество элементов, называемых вершинами, а
непустое
конечное множество элементов, называемых вершинами, а 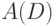 —
конечное семейство упорядоченных пар элементов из
—
конечное семейство упорядоченных пар элементов из  ,
называемых дугами (или ориентированными ребрами ). Дуга, у которой
вершина
,
называемых дугами (или ориентированными ребрами ). Дуга, у которой
вершина  является первым элементом, а вершина
является первым элементом, а вершина  — вторым, называется дугой
из
— вторым, называется дугой
из  в
в 
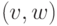 . Заметим, что
дуги
. Заметим, что
дуги 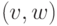 и
и  различны. Хотя графы и орграфы
— различные объекты, в определенных случаях графы можно рассматривать как орграфы, в
которых каждому ребру соответствуют две противоположно ориентированные
дуги.
различны. Хотя графы и орграфы
— различные объекты, в определенных случаях графы можно рассматривать как орграфы, в
которых каждому ребру соответствуют две противоположно ориентированные
дуги.  и
и 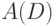 называются соответственно
множеством вершин и семейством дуг орграфа
называются соответственно
множеством вершин и семейством дуг орграфа  .
.
На (рис. 9.1) представлен орграф, дугами которого являются  . Порядок вершин
на дуге указан стрелкой. Граф, полученный из орграфа
. Порядок вершин
на дуге указан стрелкой. Граф, полученный из орграфа  удалением
стрелок, то есть заменой каждой дуги вида
удалением
стрелок, то есть заменой каждой дуги вида 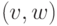 на соответствующее ребро
на соответствующее ребро  , называется основанием орграфа
, называется основанием орграфа  . Многие
определения, данные для графов, можно перенести на орграфы. К примеру, две вершины
. Многие
определения, данные для графов, можно перенести на орграфы. К примеру, две вершины 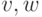 орграфа
орграфа  называются смежными, если в
называются смежными, если в 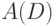 существует
дуга вида
существует
дуга вида 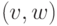 или
или  ; при этом
вершины
; при этом
вершины 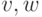 называются инцидентными любой такой дуге (а дуга — инцидентной соответствующим
вершинам ). Два орграфа называются изоморфными, если
существует изоморфизм между их основаниями, сохраняющий порядок вершин на
каждой дуге. Матрицей смежности орграфа с множеством вершин
называются инцидентными любой такой дуге (а дуга — инцидентной соответствующим
вершинам ). Два орграфа называются изоморфными, если
существует изоморфизм между их основаниями, сохраняющий порядок вершин на
каждой дуге. Матрицей смежности орграфа с множеством вершин 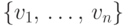 является матрица, в которой
является матрица, в которой  равно числу дуг
вида
равно числу дуг
вида 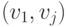 в семействе
в семействе 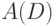 . Матрица
смежности для начерченного графа
. Матрица
смежности для начерченного графа
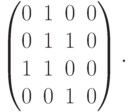
Орграфы, не
содержащие петель и кратных ребер, называются простыми. Ориентированный маршрут
в орграфе  представляет собой конечную последовательность дуг вида
представляет собой конечную последовательность дуг вида 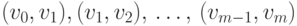 . Эту
последовательность можно записывать в виде
. Эту
последовательность можно записывать в виде  и говорить об ориентированном маршруте из
и говорить об ориентированном маршруте из  в
в 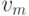 .
Аналогичным образом можно определить ориентированные цепи, ориентированные простые цепи и
ориентированные циклы — орцепи, простые орцепи и орциклы.
Заметим, что хотя орцепь не может содержать данную дугу
.
Аналогичным образом можно определить ориентированные цепи, ориентированные простые цепи и
ориентированные циклы — орцепи, простые орцепи и орциклы.
Заметим, что хотя орцепь не может содержать данную дугу 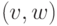 более одного раза, она может содержать одновременно
более одного раза, она может содержать одновременно 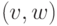 и
и  .
Например, на (рис. 9.1)
.
Например, на (рис. 9.1) 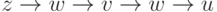 является орцепью.
является орцепью.


