| Что такое сеть? |
Орграфы
Определим два наиболее естественных и полезных типа связности орграфов,
которые возникают в соответствии с тем, хотим мы или нет принимать во
внимание ориентацию дуг. Говорят, что орграф  связен,
или слабо связен, если он не может быть представлен в виде
объединения двух различных орграфов (определенных обычным образом). Это эквивалентно
тому, что связно основание орграфа
связен,
или слабо связен, если он не может быть представлен в виде
объединения двух различных орграфов (определенных обычным образом). Это эквивалентно
тому, что связно основание орграфа  . Предположим также, что для
любых двух вершин
. Предположим также, что для
любых двух вершин 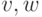 орграфа
орграфа  существует простая орцепь
из
существует простая орцепь
из  в
в  ,
тогда
,
тогда  называется сильно связным. Этот термин настолько
устоялся, что мы использовали его вместо более естественного " орсвязный ". Ясно, что любой сильно связный граф связен, но
обратное неверно. На (рис. 9.1) изображен связный орграф, не являющийся сильно
связным, так как не существует простой орцепи из
называется сильно связным. Этот термин настолько
устоялся, что мы использовали его вместо более естественного " орсвязный ". Ясно, что любой сильно связный граф связен, но
обратное неверно. На (рис. 9.1) изображен связный орграф, не являющийся сильно
связным, так как не существует простой орцепи из  в
в  .
.
Различие между связным и сильно связным орграфом станет яснее, если рассмотреть план города, по всем улицам которого допускается только одностороннее движение. Тогда связность соответствующего орграфа означает, что можно проехать из любой части города в любую другую, не обращая внимания на правила одностороннего движения. Если же этот орграф сильно связан, то можно проехать из любой части города в любую другую, следуя всегда "правильным путем" вдоль улиц с односторонним движением.
Важно, чтобы система с односторонним движением была сильно связной, и естественно возникает вопрос: при каких условиях карту улиц можно превратить в систему с односторонним движением таким способом, чтобы можно было проехать из любой части города в любую другую? Если, к примеру, город состоит из двух частей, связанных одним мостом, то мы никогда не сможем сделать все его улицы односторонними, поскольку какое бы направление ни приписали мосту, одна часть города будет отрезана. Сюда включается и тот случай, когда в городе имеется тупик. С другой стороны, если мостов нет, то всегда найдется подходящая односторонняя система; это и есть основной результат, который будет установлен ниже в теореме.
Для удобства будем называть граф  ориентируемым, если каждое
его ребро (рассматриваемое как пара вершин) может быть упорядочено таким
образом, что полученный в результате орграф будет сильно связным. Этот
процесс упорядочивания ребер будем называть заданием ориентации
графа или приписыванием направлений ребрам.
Если, например,
ориентируемым, если каждое
его ребро (рассматриваемое как пара вершин) может быть упорядочено таким
образом, что полученный в результате орграф будет сильно связным. Этот
процесс упорядочивания ребер будем называть заданием ориентации
графа или приписыванием направлений ребрам.
Если, например,  — граф, изображенный на (рис. 9.2), то его можно
ориентировать и получить сильно связный орграф, изображенный на (рис. 9.3).
— граф, изображенный на (рис. 9.2), то его можно
ориентировать и получить сильно связный орграф, изображенный на (рис. 9.3).
Мы видим, что любой эйлеров граф ориентируем, поскольку достаточно пройти по любой эйлеровой цепи, ориентируя ребра в направлении движения по ним. Дадим необходимое и достаточное условие ориентируемого графа.
Теорема 9.1 (Роббинс)
Пусть  — связный граф; он ориентируем тогда и только
тогда, если каждое его ребро содержится, по крайней мере, в одном цикле.
— связный граф; он ориентируем тогда и только
тогда, если каждое его ребро содержится, по крайней мере, в одном цикле.
Доказательство Необходимость условия очевидна. Чтобы доказать достаточность,
выберем любой цикл  и ориентируем его ребра в направлении
какого-либо обхода этого цикла. Если каждое ребро из
и ориентируем его ребра в направлении
какого-либо обхода этого цикла. Если каждое ребро из  содержится
в
содержится
в  , то доказательство завершено; если нет, то возьмем любое ребро
, то доказательство завершено; если нет, то возьмем любое ребро  , не
принадлежащее
, не
принадлежащее  , но смежное некоторому ребру из
, но смежное некоторому ребру из  .
По предположению, ребро
.
По предположению, ребро  содержится в каком-то цикле
содержится в каком-то цикле 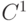 . Ребрам
цикла
. Ребрам
цикла 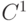 можно приписать ориентацию в направлении какого-либо обхода этого цикла
(за исключением тех ребер, которые уже были ориентированы, то есть тех
ребер из
можно приписать ориентацию в направлении какого-либо обхода этого цикла
(за исключением тех ребер, которые уже были ориентированы, то есть тех
ребер из 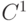 , которые принадлежат также
, которые принадлежат также  ).
Нетрудно убедиться в
том, что описанная процедура за конечное число шагов приведет к сильно
связному орграфу.
).
Нетрудно убедиться в
том, что описанная процедура за конечное число шагов приведет к сильно
связному орграфу.



