| Что такое сеть? |
Теория трансверсалей
Теория трансверсалей
Приводятся определения трансверсали. Используя эти понятия, дается еще одно доказательство теоремы Холла. Описывается несколько приложений в лексике трансверсалей.
Если  — непустое конечное множество и
— непустое конечное множество и  — семейство (не обязательно различных) непустых его
подмножеств, трансверсалью (или системой различных
представлений ) для
— семейство (не обязательно различных) непустых его
подмножеств, трансверсалью (или системой различных
представлений ) для  называется подмножество множества
называется подмножество множества  ,
состоящее из
,
состоящее из  элементов: по одному из каждого множества
элементов: по одному из каждого множества  .
.
Общие трансверсали. Если  — непустое конечное
множество, а
— непустое конечное
множество, а  и
и  — два
семейства его непустых подмножеств, то интересно знать, когда существует
общая трансверсаль для
— два
семейства его непустых подмножеств, то интересно знать, когда существует
общая трансверсаль для  и
и  , то есть
множество, состоящее из
, то есть
множество, состоящее из  различных элементов множества
различных элементов множества  и являющееся
трансверсалью и для
и являющееся
трансверсалью и для  , и для
, и для  .
.
Рассмотрим пример. Предположим, что  ,
а
,
а  ,
,  ,
,  .
Подсемейство
.
Подсемейство 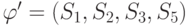 имеет
трансверсаль, например
имеет
трансверсаль, например  . Трансверсаль произвольного подсемейства
семейства
. Трансверсаль произвольного подсемейства
семейства  будем называть частичной трансверсалью
для
будем называть частичной трансверсалью
для  ; в нашем примере семейство
; в нашем примере семейство  имеет несколько
частичных трансверсалей (например,
имеет несколько
частичных трансверсалей (например, 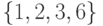 ,
,  ,
,  ,
,  и т.д.). Ясно, что любое подмножество частичной
трансверсали само является частичной трансверсалью.
и т.д.). Ясно, что любое подмножество частичной
трансверсали само является частичной трансверсалью.
Естественно спросить: при каких условиях данное семейство подмножеств
некоторого множества имеет трансверсаль? Легко увидеть связь между
этой задачей и задачей о свадьбах, если взять за Е множество девушек,
а за  — множество девушек, знакомых юноше
— множество девушек, знакомых юноше  ; трансверсалью в этом случае является множество из
; трансверсалью в этом случае является множество из  девушек,
такое, что каждому юноше соответствует ровно одна (знакомая ему) девушка.
Следовательно, теорема Холла дает необходимое и достаточное условие
существования трансверсали для данного семейства множеств. Сформулируем
теорему Холла для этого случая и дадим другое ее доказательство,
принадлежащее Р.Радо.
девушек,
такое, что каждому юноше соответствует ровно одна (знакомая ему) девушка.
Следовательно, теорема Холла дает необходимое и достаточное условие
существования трансверсали для данного семейства множеств. Сформулируем
теорему Холла для этого случая и дадим другое ее доказательство,
принадлежащее Р.Радо.
Теорема
Пусть  — непустое конечное множество и
— непустое конечное множество и 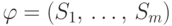 — семейство непустых его подмножеств;
тогда
— семейство непустых его подмножеств;
тогда  имеет
трансверсаль в том и только в том случае, если для любых
имеет
трансверсаль в том и только в том случае, если для любых  подмножеств
подмножеств  их объединение содержит, по меньшей мере,
их объединение содержит, по меньшей мере,  элементов
элементов 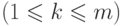 .
.
Доказательство Необходимость этого условия очевидна. Для доказательства
достаточности установим, что если одно из подмножеств (скажем,  )
содержит более одного элемента, то можно удалить один элемент из
)
содержит более одного элемента, то можно удалить один элемент из  , не нарушив условия теоремы. Повторением этой процедуры мы
добьемся сведения задачи к тому случаю, когда каждое подмножество
содержит только один элемент. Тогда утверждение станет очевидным.
, не нарушив условия теоремы. Повторением этой процедуры мы
добьемся сведения задачи к тому случаю, когда каждое подмножество
содержит только один элемент. Тогда утверждение станет очевидным.
Осталось обосновать законность этой "процедуры сведения".
Предположим,
что  содержит элементы
содержит элементы  и
и  ,
удаление каждого из которых
нарушает условие теоремы. Тогда существуют подмножества
,
удаление каждого из которых
нарушает условие теоремы. Тогда существуют подмножества  и
и  множества
множества  , обладающие тем свойством, что
, обладающие тем свойством, что

Но эти два неравенства приводят к противоречию, поскольку

Прелесть этого доказательства в том, что оно проводится, по существу, лишь в один шаг, в отличие от доказательства Халмоша-Вогена, которое предполагает исследование двух отдельных случаев. (Однако доказательство Радо труднее перевести на весьма наглядный матримониальный язык!).
Следствие
В тех же обозначениях, что и выше,  имеет частичную
трансверсаль мощности
имеет частичную
трансверсаль мощности  тогда и только тогда, если для любых
тогда и только тогда, если для любых  подмножеств
подмножеств  их объединение содержит, по меньшей мере,
их объединение содержит, по меньшей мере,  элементов.
элементов.
Доказательство
Требуемый результат можно получить, применив теорему Холла в
лексике трансверсалей к семейству 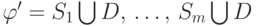 , где
, где  — произвольное множество, не
непересекающееся с
— произвольное множество, не
непересекающееся с  и состоящее из
и состоящее из  элементов. Заметим, что
элементов. Заметим, что  имеет частичную трансверсаль мощности
имеет частичную трансверсаль мощности  тогда и только тогда,
если
тогда и только тогда,
если  имеет трансверсаль.
имеет трансверсаль.
Следствие
Если  и
и  такие же, как и прежде,
а
такие же, как и прежде,
а  — любое подмножество
из
— любое подмножество
из  , то
, то  содержит частичную трансверсаль
мощности
содержит частичную трансверсаль
мощности  для
для  тогда и только тогда, если для каждого подмножества
тогда и только тогда, если для каждого подмножества  множества
множества 

Доказательство Достаточно применить предыдущее следствие
к семейству  .
.

