| Что такое сеть? |
Цепи Маркова
Еще раз об ориентированных графах
Степенью
выхода вершины  ориентированного графа называется
число выходящих из
ориентированного графа называется
число выходящих из  дуг (ребер). Степенью входа
вершины
дуг (ребер). Степенью входа
вершины  ориентированного графа называется число входящих
в
ориентированного графа называется число входящих
в  дуг (ребер).
дуг (ребер).
Изолированной вершиной называется вершина, у которой и степень
входа, и степень выхода равны  . Источником называется вершина,
степень выхода которой положительна, а степень входа равна
. Источником называется вершина,
степень выхода которой положительна, а степень входа равна  . Стоком называется вершина, степень входа которой положительна,
а степень выхода равна
. Стоком называется вершина, степень входа которой положительна,
а степень выхода равна  . Путем в ориентированном графе
. Путем в ориентированном графе  от
от 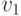 до
до 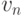 называется последовательность ориентированных дуг
(ребер)
называется последовательность ориентированных дуг
(ребер)  ,
, 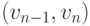 ,
такая, что конец каждой предыдущей дуги (ребра) совпадает с началом следующей и ни одна дуга
(ребро) не встречается более одного раза. Если в ориентированном
графе
,
такая, что конец каждой предыдущей дуги (ребра) совпадает с началом следующей и ни одна дуга
(ребро) не встречается более одного раза. Если в ориентированном
графе  нашелся путь от
нашелся путь от  до
до  , то обратного пути
от
, то обратного пути
от  к
к  может и не быть. Простым путем в ориентированном графе
называется путь, в котором ни одна вершина не содержится более одного
раза. Замкнутый путь в ориентированном графе называется
ориентированным циклом. Длиной пути называется число дуг (ребер) в
этом пути. Расстоянием от
может и не быть. Простым путем в ориентированном графе
называется путь, в котором ни одна вершина не содержится более одного
раза. Замкнутый путь в ориентированном графе называется
ориентированным циклом. Длиной пути называется число дуг (ребер) в
этом пути. Расстоянием от  до
до  в
ориентированном графе называется длина наикратчайшего пути от
в
ориентированном графе называется длина наикратчайшего пути от  до
до  . Если пути
от
. Если пути
от  до
до  не существует, то расстояние
от
не существует, то расстояние
от  до
до  называется
бесконечным. Оно
обозначается
называется
бесконечным. Оно
обозначается  . Расстояние от
. Расстояние от  до
до  будем обозначать
будем обозначать 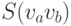 . Полным ориентированным
графом называется граф, каждая пара вершин которого соединена в точности одной
ориентированной дугой (ребром). Если с каждого ребра (дуги) полного
ориентированного графа снять направление, то образуется полный граф с
неориентированными ребрами (дугами).
. Полным ориентированным
графом называется граф, каждая пара вершин которого соединена в точности одной
ориентированной дугой (ребром). Если с каждого ребра (дуги) полного
ориентированного графа снять направление, то образуется полный граф с
неориентированными ребрами (дугами).
Задачи на круговые бескомпромиссные турниры
Напомним, что соревнование, в котором каждая из команд играет с каждой из
остальных команд в точности по одному разу, называют круговым
турниром или турниром в один круг. Если каждая встреча
оканчивается непременно выигрышем одной из команд, то круговой
турнир называется бескомпромиссным. Круговой бескомпромиссный
турнир проводится, например, в волейболе и баскетболе. Так как мы
рассматриваем исключительно бескомпромиссные круговые турниры, не
возникает опасности спутать их с каким-либо другим видом турниров; такое
соревнование будем называть сокращенно турниром. Каждому турниру
соответствует полный ориентированный граф, в котором вершины представляют
команды, а каждая ориентированная дуга 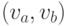 выражает
отношение "
выражает
отношение "  победила
победила  ".
Степень выхода любой вершины
".
Степень выхода любой вершины  есть число побед, одержанных
командой
есть число побед, одержанных
командой  .
.
Задача 1. Турнир по волейболу
проводится между  командами.
Докажем, что если какие-нибудь две команды одержали в турнире одинаковое
число побед, то найдутся среди участников три команды I, II, III, такие,
что I выиграла у II, II выиграла у III, а III выиграла у I.
командами.
Докажем, что если какие-нибудь две команды одержали в турнире одинаковое
число побед, то найдутся среди участников три команды I, II, III, такие,
что I выиграла у II, II выиграла у III, а III выиграла у I.
Решение. Пусть  и
и  — две команды, одержавшие
одинаковое число побед, например,
— две команды, одержавшие
одинаковое число побед, например,  побед. Пусть к тому
же
побед. Пусть к тому
же  выиграла у
выиграла у  . Те
. Те  команд, у которых выиграла
команда
команд, у которых выиграла
команда  ,
обозначим
,
обозначим  (рис. 10.1).
(рис. 10.1).
Команда  не могла одержать победы над всеми командами из
числа
не могла одержать победы над всеми командами из
числа  , так как иначе она одержала бы больше,
чем
, так как иначе она одержала бы больше,
чем  побед.
побед.
Следовательно, среди команд 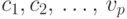 найдется
хотя бы одна, которая одержала победу над
найдется
хотя бы одна, которая одержала победу над  . Стрелку от нее
направим
. Стрелку от нее
направим  . Путь замкнется.
. Путь замкнется.
Сформулируем полученный результат на языке графов.



