| Что такое сеть? |
Цепи Маркова
Другой пример: если цепь Маркова имеет матрицу перехода, приведенную на рис. 10.8, то ассоциированный орграф этой цепи выглядит так, как показано на (рис. 10.9).

Теперь ясно, что в цепи Маркова из состояния 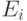 в
состояние
в
состояние 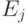 можно попасть в том и только в том случае, если в
ассоциированном
орграфе существует орцепь из
можно попасть в том и только в том случае, если в
ассоциированном
орграфе существует орцепь из 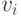 в
в 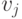 , и что
наименьшее
возможное время попадания равно длине кратчайшей из таких орцепей. Цепь
Маркова, в которой из любого состояния можно попасть в любое другое,
называется неприводимой. Ясно, что цепь Маркова неприводима тогда и
только тогда, если ее ассоциированный орграф сильно связан. Заметим,
что ни одна из описанных выше цепей не является неприводимой.
, и что
наименьшее
возможное время попадания равно длине кратчайшей из таких орцепей. Цепь
Маркова, в которой из любого состояния можно попасть в любое другое,
называется неприводимой. Ясно, что цепь Маркова неприводима тогда и
только тогда, если ее ассоциированный орграф сильно связан. Заметим,
что ни одна из описанных выше цепей не является неприводимой.
При дальнейших исследованиях принято различать те состояния, в которые мы
продолжаем возвращаться независимо от продолжительности процесса, и те,
в которые мы попадаем несколько раз и никогда не возвращаемся. Более точно
это выглядит так: если начальное состояние есть 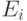 и вероятность возвращения в
и вероятность возвращения в 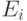 на некотором более позднем шаге равна единице,
то
на некотором более позднем шаге равна единице,
то 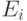 называется возвратным (или рекурсивным)
состоянием. В противном случае состояние
называется возвратным (или рекурсивным)
состоянием. В противном случае состояние 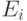 называется
невозвратным. В задаче об осле, например, очевидно, что состояния
называется
невозвратным. В задаче об осле, например, очевидно, что состояния 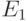 и
и 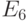 являются возвратными, тогда как все
другие состояния — невозвратными. В более сложных примерах вычисление нужных
вероятностей становится очень хитрым делом, и поэтому проще бывает
классифицировать состояния, анализируя ассоциированный орграф цепи.
Нетрудно понять, что состояние
являются возвратными, тогда как все
другие состояния — невозвратными. В более сложных примерах вычисление нужных
вероятностей становится очень хитрым делом, и поэтому проще бывает
классифицировать состояния, анализируя ассоциированный орграф цепи.
Нетрудно понять, что состояние 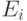 возвратно тогда и только
тогда, если существование простой орцепи из
возвратно тогда и только
тогда, если существование простой орцепи из 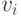 в
в 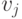 в ассоциированном орграфе влечет за собой существование простой орцепи из
в ассоциированном орграфе влечет за собой существование простой орцепи из 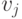 в
в 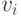 .
В орграфе, изображенном на (рис. 10.7), существует простая орцепь из
.
В орграфе, изображенном на (рис. 10.7), существует простая орцепь из 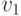 в
в 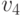 , но нет ни одной орцепи из
, но нет ни одной орцепи из 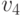 в
в 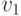 . Следовательно,
состояния
. Следовательно,
состояния 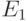 и, аналогично,
и, аналогично, 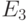 невозвратны
(
невозвратны
( 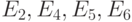 возвратны). Состояние (такое, как
возвратны). Состояние (такое, как  ), из которого нельзя попасть ни в какое другое, называется поглощающим состоянием.
), из которого нельзя попасть ни в какое другое, называется поглощающим состоянием.
Другой прием классификации состояний опирается на понятие периодичности
состояний. Состояние 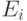 цепи Маркова называется периодическим с периодом
цепи Маркова называется периодическим с периодом 
 , если
в
, если
в 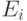 можно вернуться
только по истечении времени, кратного
можно вернуться
только по истечении времени, кратного  . Если
такого
. Если
такого  не существует, то состояние
не существует, то состояние 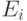 называется непериодическим.
Очевидно, что каждое состояние
называется непериодическим.
Очевидно, что каждое состояние 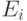 , для которого
, для которого  , непериодическое. Следовательно, каждое поглощающее состояние —
непериодическое. В задаче об осле не только поглощающее
состояние
, непериодическое. Следовательно, каждое поглощающее состояние —
непериодическое. В задаче об осле не только поглощающее
состояние  , но и все остальные являются
непериодическими. С другой стороны, во втором примере (рис. 10.9) поглощающее
состояние
, но и все остальные являются
непериодическими. С другой стороны, во втором примере (рис. 10.9) поглощающее
состояние  — единственное непериодическое состояние,
поскольку
— единственное непериодическое состояние,
поскольку 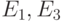 имеют период два, а
имеют период два, а  — период три. Используя терминологию орграфов, легко показать, что
состояние
— период три. Используя терминологию орграфов, легко показать, что
состояние 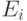 является периодическим с периодом
является периодическим с периодом  тогда и только тогда, если
в ассоциированном орграфе длина каждой замкнутой орцепи, проходящей
через
тогда и только тогда, если
в ассоциированном орграфе длина каждой замкнутой орцепи, проходящей
через 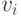 , кратна
, кратна  .
.
И, наконец, для полноты изложения введем еще одно понятие: назовем состояние цепи Маркова эргодическим, если оно одновременно возвратно и непериодично. Если любое состояние цепи Маркова является эргодическим, то назовем ее эргодической цепью.



