| ВКР |
Организация снабженческо-сбытовой деятельности ПКС на базе виртуального терминала организационно-логистической информационной системы
Товарно-материальные запасы всегда считались фактором, обеспечивающим безопасность системы материально-технического снабжения, ее гибкое функционирование, и являлись своего рода "страховкой". Особенность предпринимательских систем в том, что товары заказываются в количествах, избыточных по отношению к необходимым на данный момент объемам. Тому есть ряд причин, как то: задержка с получением заказанных товаров в полном объеме; скидки, предоставляемые при продаже товаров крупными партиями; налогообложение торговых сделок с минимальным размером партий, делающее невыгодной отправку заказчику товаров в количествах меньше установленного размера, и некоторые другие. Ограничителем выступают издержки их хранения. Определение точного уровня запасов, необходимых в условиях нестабильности сроков реализации заказов, изменчивого спроса на товары и материалы - дело нелегкое. Вероятностная природа вышеуказанных колебаний и нестабильности означает, что для нахождения удовлетворительных решений проблем необходимо соответствующее моделирование или имитация. Создание товарно-материальных запасов определяется также специфической ролью, которую играют предприятия в процессе выпуска продукции. В одних областях народного хозяйства основной задачей является контроль за сырьем, в других - за готовой продукцией или незавершенным производством.
Определим целевую функцию гарантийного запаса как функцию совокупных затрат, связанных с обслуживанием гарантийного запаса. Очевидно, функция должна быть минимизирована при условии обеспечения бесперебойного снабжения (7.9):
 |
( 7.9) |
где 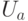 - размер гарантийного запаса;
- размер гарантийного запаса;
 - этапы производственного цикла,
- этапы производственного цикла,  - множество всех этапов производства;
- множество всех этапов производства;
 - время начала
- время начала  -го этапа производства;
-го этапа производства;
 - время окончания
- время окончания  -го этапа производства;
-го этапа производства;
 - время начала (
- время начала (  ) этапа производства;
) этапа производства;
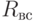 - воздействие внешней среды;
- воздействие внешней среды;
 - совокупные затраты, связанные с обслуживанием гарантийного запаса;
- совокупные затраты, связанные с обслуживанием гарантийного запаса;
 - возможный временной период между концом
- возможный временной период между концом  -го производственного этапа и началом
-го производственного этапа и началом  производственного этапа, на котором возможно использование гарантийного запаса;
производственного этапа, на котором возможно использование гарантийного запаса;
 - совокупные затраты, связанные с обслуживанием избыточного гарантийного запаса;
- совокупные затраты, связанные с обслуживанием избыточного гарантийного запаса;
 - совокупные затраты, связанные с недостаточностью гарантийного запаса.
- совокупные затраты, связанные с недостаточностью гарантийного запаса.
Минимальный размер гарантийного запаса является функцией от времени восполнения заказа и времени производства единицы  -го продукта. Очевидно, что в случае невыполнения заказа необходимо осуществление различных мер (например, поиск другого партнера), требуется время для восполнения запаса.
-го продукта. Очевидно, что в случае невыполнения заказа необходимо осуществление различных мер (например, поиск другого партнера), требуется время для восполнения запаса.
Ограничения в данной модели:
- суммарные размеры складов;
- минимальный размер гарантийного запаса с учетом прогнозируемого риска;
- минимальное время восполнения запаса потенциальным партнером с учетом его удаленности;
- минимальное время производства единицы продукции
 -го вида.
-го вида.
Задачи оптимизации времени движения материальных и информационных потоков логистической системы и оптимизации общих затрат при организации и движении материальных и информационных потоков в основе своих постановок имеют транспортную задачу в ее классическом виде, модель назначений, модель выбора кратчайшего пути и другие транспортные задачи [2, 10, 15].
Затраты на перевозку, учитывая размеры нашей страны, весьма значительны. Уменьшение этих затрат хотя бы на несколько процентов приводит к значительной экономии. Отсюда понятна важность научного подхода к проблемам перевозок. Рассмотрим самую характерную транспортную задачу. Пусть необходимо перевести однородный груз из нескольких мест. Существует бесконечное число вариантов перевозок. Естественно, необходимо найти те из них, которые соответствуют минимальным затратам на перевозку (7.10):
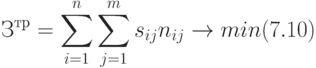 |
( 7.10) |
где 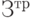 - суммарные затраты на перевозку;
- суммарные затраты на перевозку;
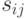 - расстояние между пунктом-отправителем
- расстояние между пунктом-отправителем  и пунктом-получателем
и пунктом-получателем  (или затраты на перевозку единицы продукции из пункта-отправителя
(или затраты на перевозку единицы продукции из пункта-отправителя  в пункт-потребитель
в пункт-потребитель  .
.
 - количество груза, перевозимого из пункта-отправителя
- количество груза, перевозимого из пункта-отправителя  в пункт-потребитель
в пункт-потребитель  .
.
Задача выбора наиболее рационального плана перевозки груза сводится к задаче линейного программирования.
На практике часто осуществляют решение транспортных задач в сетевой подстановке. Если взглянуть на карту местности, то дороги соединяют большинство пунктов не непосредственно, а проходят через другие пункты. Груз можно перевезти разными путями. Поэтому часто задачу перевозки грузов формулируют не в матричной постановке, а в так называемой постановке, основанной на явном представлении структуры транспортной сети.
Например, имеется  перенумерованных пунктов (рис. 7.6). Пункты соединены коммуникациями. Во всех пунктах задается сальдо производства и потребления. В задаче оптимизируются транспортные издержки. Целевая функция затрат по транспортным издержкам должна стремиться к минимуму (7.11).
перенумерованных пунктов (рис. 7.6). Пункты соединены коммуникациями. Во всех пунктах задается сальдо производства и потребления. В задаче оптимизируются транспортные издержки. Целевая функция затрат по транспортным издержкам должна стремиться к минимуму (7.11).
 |
( 7.11) |
где  - суммарные затраты на перевозку;
- суммарные затраты на перевозку;
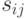 - расстояние между пунктом-отправителем
- расстояние между пунктом-отправителем  и пунктом-получателем
и пунктом-получателем  (или затраты на перевозку единицы продукции из пункта-отправления
(или затраты на перевозку единицы продукции из пункта-отправления  в пункт-потребитель
в пункт-потребитель  ;
;
 - количество груза, перевозимого из пункта-отправления
- количество груза, перевозимого из пункта-отправления  в пункт-потребитель
в пункт-потребитель  .
.
Ограничениями в данной модели являются ограничения по пропускной способности, размеры транспортного парка, максимальный размер (объем) транспортной единицы и т. п.
Для решения транспортных задач на практике часто используют метод потенциалов. Общий принцип подсчета потенциалов заключается в следующем: определяется потенциал в исходном пункте, в соседнем пункте к исходному потенциалу добавляются удельные затраты на перевозку, если движение осуществляется против направления перевозки - то вычитаются. Сумма по всем вершинам произведения потенциала на сальдо производства и потребления дает значение критерия задачи для данного плана. Для уменьшения значения критерия необходимо уменьшить потенциалы в пунктах-потребителях.
Итак, рассмотрен ряд моделей организации ССД. Их количества на практике, естественно, гораздо больше. Полностью смоделировать деятельность по снабжению, сбыту возможно, если известны компоненты организационной структуры ВКС, технологические особенности, географическое расположение и др. Моделирование технологических цепочек, определение оптимального взаимодействия с точки зрения минимизации совокупных издержек позволяет наиболее эффективным образом организовать снабженческо-сбытовую деятельность ВКС. В оптимизации складской деятельности (рациональный выбор местоположения склада, его размеров, решение вопросов об использовании собственных складов или аренде, возможности пользования услугами специализированных компаний, рациональное размещение продукции на складе, выбор рациональных подъездных путей и т. п.) также можно использовать сетевые графики для решения задач и другие методы, подробным образом рассмотренные в работах по экономико-математическому моделированию управления запасами [11, 13, 20, 34, 35].
Таким образом, модель СОЗ ССД ВКС представляет собой совокупность целевых задач. Для нахождения эффективного управленческого решения необходимо комплексное решение СОЗ с учетом взаимосвязей и взаимозависимостей. На следующем шаге рассмотрим алгоритм решения системы оптимизационных задач ССД ВКС (рис. 7.6). По условиям запроса множество целевых функций фильтруется, определяется СОЗ, решение которой необходимо в конкретной производственной ситуации. Совокупность ограничений отобранных целевых функций анализируется, определяется область допустимых значений (ОДЗ) и область определения функций (ООФ), т. е. определяется область поиска оптимального решения СОЗ. Находится вектор приоритетности целевых задач, сортировка в порядке убывания приоритетности, последовательное решение СОЗ. Пересечение множеств оптимальных планов отдельных задач определяет оптимальный план СОЗ. Полученный план передается ЛПР в виде текстовой или графической информации для выработки управленческого решения. Если область пересечения является пустым множеством, осуществляется выбор метода и решение многокритериальной задачи. Более подробное изложение данного материала рассматривается ниже при описании алгоритма организации ССД ВКС на базе ВИТ ОЛИС. Итак, императив развития антикризисного реформационного процесса - создание новых и повышение действенности сложившихся корпоративных структур. Концепция ВКС - новая форма взаимодействия предприятий. За счет высокой адаптивности к рыночным условиям ВКС позволяет осуществить выпуск наиболее конкурентоспособной продукции, завоевать утерянные сегодня рынки сбыта, повысить рентабельность отечественной экономики. Управление таким сложным объектом невозможно без использования ИС, в основе проектирования которой используются принципы логистики. Формирование управленческих решений требует централизованного сбора и обработки информации о снабженческо-сбытовой деятельности. Таким механизмом предлагается использовать виртуальный информационный терминал ССД. Цель функционирования системы определяет ее задачи, решение которых способствует достижению поставленных целей. Анализ деятельности корпоративной структуры осуществляется с помощью множества показателей, выбор которых необходимо осуществлять с точки зрения целей и задач корпорации. Предлагаемая система показателей позволяет наиболее полно проанализировать ССД ВКС. Система задач организации ССД ВКС является многоуровневой системой, представляет собой многокритериальную задачу. Комплексное решение системы целевых функций, определение оптимального плана, удовлетворяющего всем задачам, позволяет найти наиболее эффективное решение, что обеспечит высокую степень согласованности ресурсных потоков, минимизировать совокупные издержки.


