| ВКР |
Организация снабженческо-сбытовой деятельности ПКС на базе виртуального терминала организационно-логистической информационной системы
В современных рыночных условиях важное значение в ССД приобретает маркетинговая деятельность. Анализ рынка учитывается при составлении производственной программы, при составлении планов и графиков по снабжению и сбыту. События на рынке носят вероятностный характер, поэтому на практике при моделировании различных экономических явлений используют методы прогнозирования. Данные методы достаточно хорошо изучены и широко представлены в литературе [31, 34, 35].
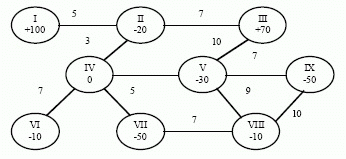
ВКС - сложный, динамичный объект, изменяющий свою организационную структуру на протяжении всего жизненного цикла проекта. Одна из важных задач ССД ВКС - выбор оптимального состава участников проекта.
Под реализацию проекта интегрируется ряд предприятий, причем для эффективного функционирования корпоративной структуры необходим оптимальный выбор участников - предприятий, которые могут выполнить проект и выполнить его наиболее эффективным образом. ВКС - динамичная структура. В связи с этим важное значение приобретает контроль деятельности участников ВКС, анализ потенциальных участников, расчет наиболее выгодной организационной структуры, принятие своевременных мер (рациональное изменение организационной структуры ВКС) в случае необходимости.
В работе [14] предлагается метод отбора участников корпоративной структуры. Создание модели осуществляется путем среза основного множества претендентов и получения наборов групп, проверки полученных наборов на жизнеспособность. Этот процесс состоит из следующих этапов:
- цель формирования группы;
- подбор претендентов, чье участие в группе отвечает цели ее создания;
- анализ предложенных структур.
Выбор осуществляется с использованием теории нечетких множеств, поскольку ранее существующие методы и модели не учитывают фактор неполноты, неточности данных об участниках проекта.
Специфика каждой из задач ССД требует использования совершенно определенных методов. Задача оптимизации запасов готовой продукции [19, 20] является важной задачей (особенно в динамично изменяемых рыночных условиях) в системе задач управления запасами.
В качестве целевой функции  принимаем суммарные затраты на производство и содержание готовой продукции при условии полного и своевременного удовлетворения спроса. Очевидно, затраты должны быть минимальны (формула (7.2)).
принимаем суммарные затраты на производство и содержание готовой продукции при условии полного и своевременного удовлетворения спроса. Очевидно, затраты должны быть минимальны (формула (7.2)).
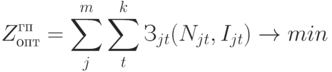 |
( 7.2) |
где  ;
; 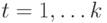
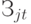 - совокупные затраты на производство и содержание готовой продукции
- совокупные затраты на производство и содержание готовой продукции  -го вида на рассматриваемый период.
-го вида на рассматриваемый период.
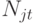 - объем выпуска
- объем выпуска  -го вида продукции на рассматриваемый период;
-го вида продукции на рассматриваемый период;
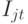 - уровень запасов
- уровень запасов  -го вида продукции на конец рассматриваемого периода;
-го вида продукции на конец рассматриваемого периода;
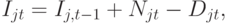
где 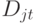 - спрос на продукцию
- спрос на продукцию  -го вида за рассматриваемый период времени.
-го вида за рассматриваемый период времени.
Если функции затрат линейно зависят от переменных, то решение отыскивается, например, с помощью симплексметода. При нелинейности задача формулируется в терминах динамического программирования.
Ограничениями данной модели являются:
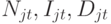 - целые положительные числа.
- целые положительные числа.
Задача определения оптимального размера партии заказа является не менее важной задачей в управлении запасами. Для оптимизации издержек пополнения запасов можно использовать известные модели по расчету партий поставок и заказов. Например, в работе [2, 20] (наиболее часто используется на практике) рассматривается следующий метод определения оптимального размера партии заказа наиболее.
Предлагается формула (7.3) расчета суммарных годовых затрат
 |
( 7.3) |
где  - суммарные годовые затраты;
- суммарные годовые затраты;
 - затраты на поставку одного заказа;
- затраты на поставку одного заказа;
 - годовой спрос;
- годовой спрос;
 - количество единиц продукции в одной партии;
- количество единиц продукции в одной партии;
 - цена единицы закупаемой продукции;
- цена единицы закупаемой продукции;
 - годовые затраты на содержание единицы продукции;
- годовые затраты на содержание единицы продукции;
 - средний объем запасов.
- средний объем запасов.
На основании соотношения (7.3) оптимальный размер партии заказа  вычисляется по формуле квадратного корня:
вычисляется по формуле квадратного корня:
 |
( 7.4) |
Графическое представление суммарных издержек за период времени и определение оптимального размера поставки представлены на рис. 7.3.
Данная модель имеет большое количество ограничений:
- рассмотрен годовой период времени;
- постоянный годовой спрос;
- неизменное количество единиц в одной партии в течение года;
- неизменная цена единицы закупаемой продукции в течение года;
- неизменные годовые затраты на содержание единицы продукции;
- постоянный в течение года темп потребления.
Поэтому рассмотрим данную задачу с учетом динамики снабженческо-производственно-сбытового процесса, влияния рынка, с учетом вхождения СПСС в ВКС.
В качестве целевой функции выберем функцию суммарных затрат, связанных с обслуживанием партии заказанного продукта. Суммарные затраты состоят из трех составляющих: затраты, связанные с ценой закупаемого продукта; затраты, связанные с транспортировкой и его хранением.
Целевую функцию суммарных затрат 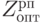 можно представить в следующей виде (7.5):
можно представить в следующей виде (7.5):
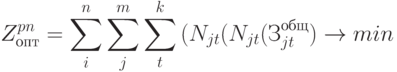 |
( 7.5)) |
где 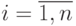 ;
; 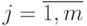 ;
; 
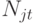 - объем выпуска
- объем выпуска  -го вида продукции на рассматриваемый период;
-го вида продукции на рассматриваемый период;
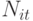 - объем выпуска
- объем выпуска  -го вида продукции на рассматриваемый период;
-го вида продукции на рассматриваемый период;
 - совокупные затраты, связанные со снабжением продуктом
- совокупные затраты, связанные со снабжением продуктом  -го вида для производства продукции
-го вида для производства продукции  -го вида за рассматриваемый период времени (7.6):
-го вида за рассматриваемый период времени (7.6):
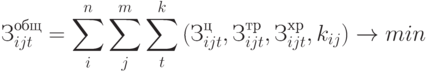 |
( 7.26) |
где 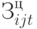 - совокупные затраты, связанные с ценой закупаемого продукта
- совокупные затраты, связанные с ценой закупаемого продукта  -го вида для производства продукции
-го вида для производства продукции  -го вида за рассматриваемый период времени;
-го вида за рассматриваемый период времени;
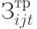 - совокупные затраты, связанные с транспортировкой закупаемого продукта
- совокупные затраты, связанные с транспортировкой закупаемого продукта  -го вида для производства продукции
-го вида для производства продукции  -го вида за рассматриваемый период времени;
-го вида за рассматриваемый период времени;
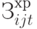 - совокупные затраты, связанные с хранением закупаемого продукта
- совокупные затраты, связанные с хранением закупаемого продукта  -го вида для производства продукции
-го вида для производства продукции  -го вида за рассматриваемый период времени;
-го вида за рассматриваемый период времени;
 - коэффициент, учитывающий возможность снижения затрат, связанную с вхождением предприятия в корпоративную структуру.
- коэффициент, учитывающий возможность снижения затрат, связанную с вхождением предприятия в корпоративную структуру.
Затраты, связанные с ценой поставки, зависят от размера партии поставки, цены за единицу продукта. Цена за единицу в свою очередь зависит от характеристик продукта, характеристик предприятия-изготовителя этого продукта.
Затраты, связанные с транспортировкой, зависят от размера транспортируемой партии, характеристик транспортируемого продукта (объем, хрупкость и т. п.), характеристик транспортной службы, определяющих стоимость транспортировки, затрат, связанных с ценой горюче-смазочных материалов, и т. п. расходы.
Затраты, связанные с хранением заказанной партии, зависят от размера партии поставки, характеристик продукта, особенностей складского хозяйства.
Ограничениями в данной модели являются:
- потребность в
 -м ресурсе для производства
-м ресурсе для производства  -го продукта;
-го продукта; - количество выделенных бюджетных средств на приобретение
 -го вида ресурса;
-го вида ресурса; - возможности транспортного парка по грузоперевозке;
- размеры складов;
- возможный объем выпускаемой продукции предприятием-поставщиком;
- возможный объем выпускаемой продукции предприятием-потребителем.
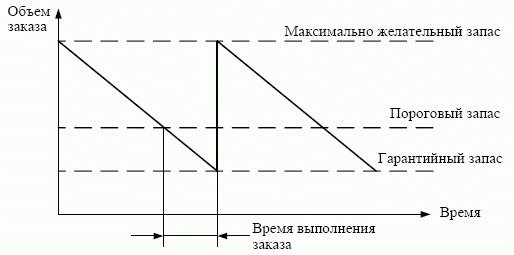
Основой для решения задач оптимизации временных интервалов между заказами являются две системы управления запасами: система с фиксированным размером заказа и система с фиксированным интервалом между заказами [3, 12, 19, 20]. Задачи оптимизации времени движения и оптимизации общих затрат в своей основе имеют транспортную задачу в ее классическом виде, модель назначений, модель выбора кратчайшего пути и другие задачи транспортного типа. Заказ делается с упреждением, равным времени выполнения заказа (рис. 7.4) [2,15].
Задача определения оптимального времени выполнения заказа сводится к минимизации совокупных затрат, связанных с обслуживанием заказа (7.7):
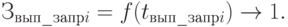 |
( 7.7) |
Время выполнения заказа представим следующей формулой (7.8):
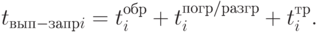 |
( 7.8) |
где 
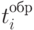 - время обработки
- время обработки  -го запроса;
-го запроса;
 - время погрузочно/разгрузочных работ по
- время погрузочно/разгрузочных работ по  -му запросу;
-му запросу;
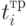 - время транспортировки по
- время транспортировки по  -му запросу.
-му запросу.
Время выполнения запроса зависит от степени автоматизации склада (наличие ПЭВМ, необходимого программного обеспечения, развитых средств коммуникаций и т. п.), степени оснащенности современными погрузочно/разгрузочными механизмами, наличия персонала достаточной квалификации, выбора оптимального способа выполнения работ. Увеличение дальности перевозок, их количества увеличивает транспортные издержки. Перевозка большими партиями, но более дешевым видом транспорта требует в дальнейшем их сохранности, что увеличивает затраты, связанные с хранением.
Ограничения данной модели:
- объем транспортного парка по грузоперевозке;
- размеры складов;
- количество погрузочно-разгрузочных механизмов;
- количество персонала на транспорте и складах.
Другая важная задача, обеспечивающая эффективное бесперебойное функционирование производства, влияющая на издержки ССД, - определение гарантийного запаса предприятий-потребителей. Гарантийный запас - "аварийный" источник снабжения в тех случаях, когда спрос на данный продукт превышает ожидание. Необходимость в гарантийном запасе диктуется сезонными изменениями цен, инфляцией, возможностью политического, экономического изменения в стране и т. д.
Для организации бесперебойного снабжения производства на практике используется несколько видов запасов. Максимально желательный запас определяет уровень запаса, экономически целесообразный для предприятия. Пороговый уровень используется для определения времени выполнения очередного заказа. Гарантийный запас предназначен для непрерывного снабжения в случае непредвиденных обстоятельств. На системы управления запасами влияет множество факторов, вызывающих колебания величины параметров, становящихся таким образом случайными величинами. Случайной величиной может быть потребление и поступление материалов, время выполнения заказа. В литературе предлагаются модели расчета страхового запаса с использованием математической теории вероятностей [20, 33, 29]. В нашем случае необходимо также учесть динамичность рынка, особенность вхождения предприятий в корпоративную структуру. Необходимо определить оптимальное соотношение между значением гарантийного запаса, обеспечивающего бесперебойное снабжение производства в случае непредвиденных ситуаций, носящих вероятностный характер, и значением совокупных затрат, которые необходимо свести к минимуму. Проанализируем факторы, влияющие на размер гарантийного запаса.


![Определение оптимального размера партии заказа [2]](/EDI/27_01_19_1/1548541181-9080/tutorial/568/objects/7/files/07_03.gif)