| ВКР |
Организация снабженческо-сбытовой деятельности ПКС на базе виртуального терминала организационно-логистической информационной системы
Применение методов многокритериальной оптимизации. Поскольку для эффективной организации ССД необходимо комплексное решение множества задач, модель ССД ВКС представляем как систему оптимизационных задач. Критерии оптимальности целевых функций, образующих систему, различны. Поэтому модель ССД ВКС - многокритериальная модель. Решением такой модели должен быть оптимизационный план, наиболее оптимальным образом удовлетворяющий всем задачам системы.
К общей формулировке многокритериальной задачи могут сводиться задачи различного содержания, которые можно подразделить на четыре типа.
- Задачи оптимизации на множестве целей, каждая из которых должна быть учтена при выборе оптимального решения.
- Задачи оптимизации на множестве объектов, качество функционирования каждого из которых оценивается самостоятельным критерием. Если качество функционирования каждого объекта оценивается несколькими критериями, такая задача называется многовекторной.
- Задачи оптимизации на множестве условий функционирования. Задан спектр условий, в которых предстоит работать объекту, и применительно к каждому условию качество функционирования оценивается некоторым частным критерием.
- Задачи оптимизации на множестве этапов функционирования. Рассматривается функционирование объектов на некотором интервале времени, разбитом на несколько этапов. Качество управления на каждом этапе оценивается частным критерием, а на множестве этапов - общим векторным критерием.
Кроме того, модель ССД ВКС - многоуровневая модель. Необходимо решение оптимизационных задач как на уровне отдельных производственных звеньев, на уровне всего предприятия, так и на уровне корпоративной структуры. При формировании обобщенных критериев должны учитываться местные критерии, а локальные подчиняться обобщенному.
Уровни модели ССД можно представить следующим образом.
Верхний уровень модели содержит модули, решение которых необходимо для организации стратегического и оперативного управления корпоративной структурой. К таким задачам можно отнести задачи стратегического менеджмента и маркетинга (например, задачи определения потенциальных участников, анализа деятельности входящих в ВКС предприятий, внешних поставщиков, потребителей и т. д.).
Нижний уровень модели включает совокупность модулей. Их решение позволяет эффективно организовать взаимодействие между предприятиями. К задачам этого уровня можно отнести совокупность задач оптимизации технологических цепочек ССД (например, задачи определения оптимального размера гарантийного запаса определенного вида ресурса, оптимального размера поставки, времени между поставками, оптимизация деятельности транспортной службы, складского хозяйства и т. д.).
С учетом вышеизложенного материала система оптимизационных задач ССД ВКС - это многоуровневая многокритериальная модель.
Для принятия оптимального решения необходимо решение комплекса задач, удовлетворяющих всем целям и ограничениям. Рассмотрим модель СОЗ ССД в общем виде (7.1). Решение одной оптимизационной задачи может являться исходными данными для решения другой, решения могут быть взаимоисключающими, разнонаправленными, инвариантными. Необходимо комплексное решение и нахождение плана, наиболее оптимальным образом удовлетворяющего всем задачам системы.
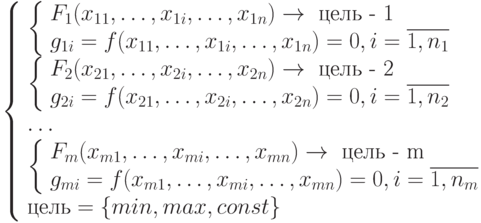 |
( 7.1) |
В настоящее время известен ряд методов [35] решения задач многокритериальной оптимизации, например:
- оптимизация одного признанного наиболее важным критерия, остальные критерии при этом играют роль дополнительных ограничений;
- упорядочение заданного множества критериев и последовательная оптимизация по каждому из них (метод последовательных уступок);
- сведение многих критериев к одному введением экспертных весовых коэффициентов для каждого из критериев таким образом, что более важный критерий получает более высокий вес;
- выделение множества недоминируемых альтернатив (множества Парето).
При разработке методов решения многокритериальных задач приходится решать ряд специфических проблем.
Проблема нормализации возникает в связи с тем, что локальные критерии имеют, как правило, различные единицы измерения, и это делает невозможным их непосредственное сравнение. Операция приведения критериев к единому масштабу и безразмерному виду носит названия нормирования. Наиболее распространенным способом нормирования является замена абсолютных значений критериев их безразмерными относительными величинами

 - оптимальное значение критерия;
- оптимальное значение критерия;
 - безразмерная величина критерия,
- безразмерная величина критерия,
или относительными значениями отклонений от оптимальных значений критериев  (т. е. переход к стандартизованным переменным)
(т. е. переход к стандартизованным переменным)

Проблема выбора принципа оптимальности связана с определением свойств оптимального решения и решения вопроса - в каком именно смысле оптимальное решение превосходит все остальные. Проблема учета приоритета критериев встает, если локальные критерии имеют различную значимость. Необходимо найти математическое определение приоритета и степень его влияния на решение задачи. Проблема вычисления оптимума возникает, если традиционные вычислительные схемы и алгоритмы непригодны для решения задачи векторной оптимизации. Решение перечисленных проблем идет в нескольких направлениях. Основные направления - это:
- методы, основанные на свертывании критериев в единый;
- методы, использующие ограничения на критерии;
- методы целевого программирования;
- методы, основанные на отыскании компромиссного решения;
- методы, в основе которых лежат человекомашинные процедуры принятия решений (интерактивное программирование).
В методах, основанных на свертывании критериев, из локальных критериев формируется один. Наиболее распространенным является метод линейной комбинации частных критериев. Задается вектор весовых коэффициентов критериев  , характеризующих важность соответствующего критерия. Линейная функция представляет собой сумму частных критериев, умноженных на весовые коэффициенты. Задача математического программирования становится однокритериальной и имеет вид:
, характеризующих важность соответствующего критерия. Линейная функция представляет собой сумму частных критериев, умноженных на весовые коэффициенты. Задача математического программирования становится однокритериальной и имеет вид:

Критерии в свертке могут быть нормированы. Решение, полученное в результате оптимизации скаляризованного критерия, эффективно.
К недостаткам метода можно отнести то, что малым приращениям коэффициентов соответствуют большие приращения функции, т. е. решение задачи неустойчиво, а также необходимость определения весовых коэффициентов.
Направление методов, использующих ограничения на критерии, включает два подхода:
- метод ведущего критерия;
- методы последовательного применения критериев (метод последовательных уступок, метод ограничений).
В методе ведущего критерия все целевые функции, кроме одной, переводятся в разряд ограничений. Полученное решение необходимо проверить на принадлежность области компромиссов.
Алгоритм метода последовательных уступок:
- Критерии нумеруются в порядке убывания важности.
- Определяется значение
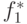 . Лицом, принимающим решение, устанавливается величина уступки
. Лицом, принимающим решение, устанавливается величина уступки  по этому критерию.
по этому критерию. - Решается задача по критерию
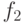 с дополнительным ограничением
с дополнительным ограничением
Далее пункты 2, 3 повторяются для критерия  .
.
Итак, при решении многокритериальных задач разработан ряд методов, которыми можно пользоваться для нахождения оптимального плана, удовлетворяющего всем задачам модели наиболее оптимальным образом.
Основные задачи ССД ВКС. На следующем шаге рассмотрим ряд основных задач ССД ВКС. Прежде отметим следующее: по содержанию различают экономико-математические и экономико-статистические модели. Экономико-математические модели включают в себя систему ограничений, целевую функцию. При организации ССД необходимо решить большое количество взаимосвязанных оптимизационных задач (табл. 7.5). При этом каждая из задач может оптимизироваться отдельно по своим локальным критериям оптимальности. В качестве глобального критерия оптимальности следует принимать показатель, учитывающий потребности рынка и обеспечивающий "выживание" в условиях конкуренции, а также получение необходимой прибыли для ВКС с учетом накладываемых ограничений. Экономико-статистические модели связаны с показателями, сгруппированными различными способами. Статистические модели устанавливают зависимость между показателями и определяющими их факторами в виде функции. В табл. 7.6 представлены некоторые статистические модели ССД. Данная таблица в дальнейшем будет являться базовой при проектировании базы данных оптимизационных задач ССД.
| Вид деятельности | Параметр | Оптимизационная задача |
|---|---|---|
| Снабжение | Пространство и время | Оптимальное время поставки в цепи поставщикпотребитель (продолжительность). Оптимальное время между поставками в цепи поставщикпотребитель (ритмичность поставок) и т. д. |
| Количество |
|
|
| Производство | Пространство и время |
|
| Количество |
|
|
| Сбыт | Пространство и время | Оптимальное время выполнения заказа на предприятии и т. д. |
| Количество | Оптимальное количество реализованного  -го вида продукта на предприятии за рассматриваемый период и т. д. -го вида продукта на предприятии за рассматриваемый период и т. д. |
|
| Складирование | Пространство и время | Оптимальное время выполнения заказа (обработка, погрузка, разгрузка, учет, размещение, хранение) на предприятии и т. д. |
| Количество |
|
|
| Транспортировка | Пространство и время | Оптимальное время транспортировки (вид транспорта, маршрут, количество перевозимого товара за один раз и т. п.) между предприятиями |
| Количество | Оптимальный товарооборот транспортной службы. Оптимальный размер единичной перевозки отдельного вида продукта. Оптимальный размер собственной транспортной службы. Оптимальный размер арендуемой транспортной службы и т. д. |
Итак, при организации ССД ВКС необходимо решение большого количества задач, причем для формирования эффективных управленческих решений необходим комплексный анализ процессов ССД.
| Задача | Функциональная зависимость | Параметры |
|---|---|---|
| Определение оптимального размера партии заказа | 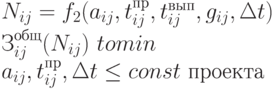 |
|
| Определение оптимального времени выполнения заказа |  |
|
| Определение оптимального размера гарантийного запаса |  |
|


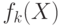 -
- -го вида ресурса в цепи поставщикпотребитель.
-го вида ресурса в цепи поставщикпотребитель. -размер партии заказа;
-размер партии заказа; - количество
- количество  - количество единиц
- количество единиц 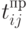 - время производства
- время производства  - время выполнения заказа (доставки
- время выполнения заказа (доставки  -размер страхового запаса
-размер страхового запаса  - совокупные затраты, связанные с обслуживанием партии поставки
- совокупные затраты, связанные с обслуживанием партии поставки 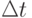 - рассматриваемый период времени.
- рассматриваемый период времени. - время выполнения заказа;
- время выполнения заказа; - время погрузочных работ;
- время погрузочных работ; - время разгрузочных работ;
- время разгрузочных работ; - время учета;
- время учета; - время транспортировки;
- время транспортировки; - вид транспорта;
- вид транспорта;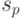 - удаленность;
- удаленность; - характеристики продукта;
- характеристики продукта;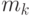 - вид маршрута;
- вид маршрута; - рассматриваемый период времени;
- рассматриваемый период времени; -степень автоматизации/механизации;
-степень автоматизации/механизации; - степень квалифицированности персонала;
- степень квалифицированности персонала;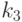 - степень оснащенности кадровым ресурсом и возможность немедленного выполнения работы;
- степень оснащенности кадровым ресурсом и возможность немедленного выполнения работы;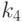 - степень загруженности складских площадей;
- степень загруженности складских площадей;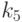 - степень загруженности оборудования (возможность немедленного выполнения работ в текущий момент);
- степень загруженности оборудования (возможность немедленного выполнения работ в текущий момент); - рассматриваемый период времени.
- рассматриваемый период времени. - размер гарантийного запаса;
- размер гарантийного запаса; - отклонение от нормативного времени производства
- отклонение от нормативного времени производства  - отклонение от нормативного времени производства
- отклонение от нормативного времени производства  - отклонение от нормативного времени доставки
- отклонение от нормативного времени доставки  - коэффициент, учитывающий другие возможные причины для формирования гарантийного запаса
- коэффициент, учитывающий другие возможные причины для формирования гарантийного запаса