| Высшее образование |
Статистическое моделирование
3.11. Способы продвижения модельного времени
При реализации имитационной модели используются обычно три представления времени:
- реальное время системы, функционирование которой имитируется;
- модельное время, по которому организуется синхронизация событий в модели;
- машинное время имитации, отражающее затраты ресурса времени компьютера.
Время в компьютерной модели принципиально не может протекать непрерывно. В компьютере в каждый момент времени выполняется одна команда. Но даже отдельные события реального процесса, протекающие, скажем, одновременно и мгновенно, в имитационной модели представляются цепочкой команд, на выполнение которых тратится машинное время.
Следовательно, время в модели, то есть модельное время (МВ), продвигается дискретно, скачками.
Продвижение времени в модели может быть организовано двумя способами:
- продвижение модельного времени с фиксированным переменным шагом
 ;
; - продвижение модельного времени до очередного события (по принципу
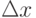 ).
).
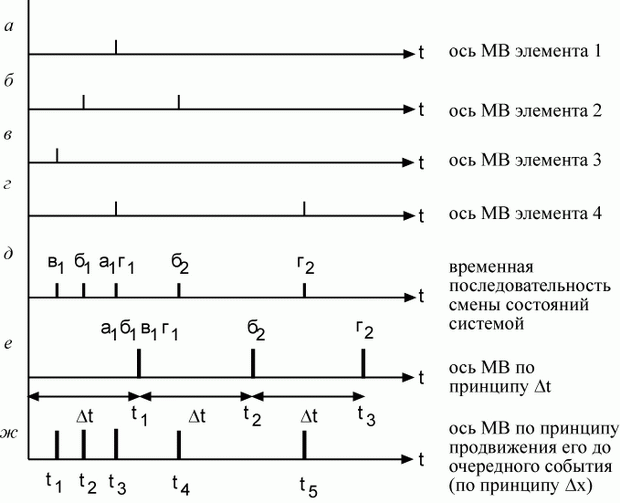
Сущность первого способа поясним временными диаграммами, показанными на рис. 3.21.
На диаграммах а…г показаны моменты смены дискретных состояний элементами 1…4 системы. На диаграмме д - временная последовательность смены состояний системой. На диаграмме е - точки модельного времени, то есть время смены состояний системы, показанных на диаграмме д.
Так как моменты модельного времени на диаграмме е не связаны с моментами появления событий а…г, то имитационная модель с фиксированным шагом продвижения времени искажает действительные процессы в системе: разновременные события представляются одновременными, моменты свершения событий фиксируются, как правило, с опозданием. Уменьшая величину  , можно уменьшить искажение действительного процесса. Однако это приводит к увеличению затрат машинного времени, особенно, если интервалы между сменами состояний в среднем больше, чем
, можно уменьшить искажение действительного процесса. Однако это приводит к увеличению затрат машинного времени, особенно, если интервалы между сменами состояний в среднем больше, чем  .
.
На диаграмме ж рис. 3.20 демонстрируется сущность второго способа. Она заключается в том, что модельное время сдвигается вперед не на фиксированную величину  , а точно до времени наступления самого раннего из очередных событий - на
, а точно до времени наступления самого раннего из очередных событий - на 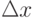 .
.
Видно, что недостатки, присущие первому способу, здесь исключены: события рассматриваются и моделируются в моменты их свершения, и одновременно (события a1,г1), если у них одинаковое время появления. Промежутки времени, когда в модели "ничего не происходит", пропускаются без особых затрат машинного времени. Эти пропуски все равно учитываются в модельном времени.
Однозначных рекомендаций по выбору того или иного способа продвижения модельного времени нет. Из общих рассуждений можно установить, что, если смена состояний в моделируемой системе происходит регулярно и часто, нет ограничений на расход машинного времени, то продвижение модельного времени фиксированными шагами  вполне приемлемо.
вполне приемлемо.
Если же смена состояний происходит редко и нерегулярно, кроме того, предъявляются повышенные требования к точности моделирования, то целесообразней второй способ продвижения модельного времени - скачками до ближайшего по времени события.
Мы рассмотрели способы продвижения модельного времени при так называемом последовательном (квазипараллельном) имитационном моделировании, характерным признаком которого является наличие централизованного списка событий и глобальных часов модельного времени. Обычно в таких имитационных моделях исследуемого процесса устанавливаются (или определяются) реальные затраты времени в масштабе, который устанавливает сам исследователь. Как правило, эти затраты безотносительны к естественному движению времени, которое обычно называют "реальным", хотя правильнее называть его естественным или натуральным.
Однако встречаются имитационные модели, которые предназначены для работы в реальном (естественном) масштабе времени. Это, например, некоторые типы тренажеров, работающие в интерактивном режиме с человеком. Заметим, что и в этом случае модельное время продвигается скачками - способом  или
или 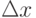 . Следовательно, возникает проблема синхронизации модельного времени с естественным временем.
. Следовательно, возникает проблема синхронизации модельного времени с естественным временем.
Существует также понятие распределенного имитационного моделирования. Источниками его развития являются: модели, требующие для своего выполнения большого количества вычислительных ресурсов, военные приложения и компьютерные игры с использованием Интернет.
Под распределенным имитационным моделированием понимается распределенное выполнение единой программы имитационной модели на мультипроцессорной или мультикомпьютерной системе.
Последовательная имитационная модель может быть выполнена на параллельной вычислительной технике. Достижение выигрыша во времени возможно за счет параллельного выполнения событий, запланированных на один и тот же момент модельного времени. При распределенном моделировании параллельно выполняются события, запланированные в различных отрезках модельного времени.
Целью использования распределенного моделирования для военных приложений является интеграция отдельно разработанных моделей в единое модельное окружение. Примером могут быть тренажеры для обучения и имитации сценариев военных действий.
Другим примером являются модели инфраструктур, объединяющие экономические, экологические, транспортные и другие подмодели. Такие подмодели могут исполняться на географически распределенных гетерогенных мультикомпьютерных системах.
Пример 3.11. На узел связи поступают заявки на передачу сообщений. Интервалы времени поступления заявок подчинены показательному закону с математическим ожиданием  . На узле связи имеются два канала передачи данных. При поступлении очередной заявки в интервале времени
. На узле связи имеются два канала передачи данных. При поступлении очередной заявки в интервале времени ![[0\ldots T_{2}]](/sites/default/files/tex_cache/4210fd5c509403b62b0c1f8c5f49339a.png) вероятности того,
вероятности того,
что каналы А и В будут свободны, соответственно равны 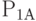 и
и 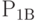 . При поступлении заявок после времени
. При поступлении заявок после времени 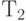 вероятности того, что каналы А и В будут свободны, соответственно равны
вероятности того, что каналы А и В будут свободны, соответственно равны 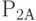 и
и 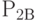 . Сообщение передаётся по любому свободному каналу. Если оба канала заняты, заявка теряется.
. Сообщение передаётся по любому свободному каналу. Если оба канала заняты, заявка теряется.
Построить алгоритм имитационной модели "Обработка запросов на узле связи" с целью определения абсолютного и относительного числа обслуженных заявок из их общего количества, поступивших на узел связи за время  ,
, 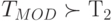 .
.
Решение
В ранее рассмотренных постановках задач отсутствовала динамика или фактор времени. Например, просто указывалось, что поступает такое-то количество заявок, а за какое время и с какими интервалами - неизвестно. Настоящая постановка задачи отличается тем, что в нее введена динамика - определены интервалы времени поступления заявок, подчиненные показательному закону.
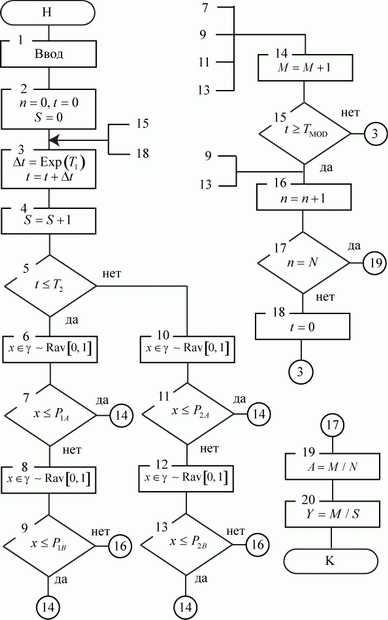
Алгоритм модели приведен на рис. 3.22.
В алгоритме модели:
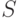 - суммарное количество заявок, поступивших за
- суммарное количество заявок, поступивших за  реализаций модели;
реализаций модели;
 - заданное количество реализаций модели;
- заданное количество реализаций модели;
 - счетчик текущего числа реализаций модели;
- счетчик текущего числа реализаций модели;
 - суммарное число обслуженных заявок за
- суммарное число обслуженных заявок за  реализаций;
реализаций;
 - абсолютное число обслуженных заявок;
- абсолютное число обслуженных заявок;
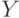 - относительное число обслуженных заявок.
- относительное число обслуженных заявок.
В связи с введением фактора времени следует обратить внимание на то, что алгоритм модели содержит два цикла: первый,
внутренний определяется временем моделирования  (блок 15), а второй, внешний - количеством реализаций модели
(блок 15), а второй, внешний - количеством реализаций модели  (блок 17).
(блок 17).
Алгоритм модели относительно прост. Но если увеличить количество элементов и различных процессов системы, ввести их динамику, например, обслуживания заявок, то алгоритм модели усложнится. Для построения имитационных моделей функционирования сложных систем "лобовой" подход неприемлем.
Далее мы рассмотрим способы, позволяющие в некотором роде унифицировать построение моделей сложных систем с продвижением в них модельного времени по принципу  или
или 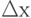 , а также до ближайшего события.
, а также до ближайшего события.

 - текущее
- текущее