| Высшее образование |
Статистическое моделирование
3.5. Моделирование случайной величины с произвольным законом распределения
В основе моделирования случайных величин с произвольными законами распределения вероятностей лежит, как правило, метод обратной функции.
В этом методе используется следующая теорема.
Теорема. Если случайная величина 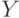 имеет плотность распределения вероятностей
имеет плотность распределения вероятностей  , то распределение случайной величины
, то распределение случайной величины
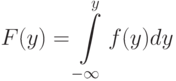 |
( y)dy) |
равномерно в интервале ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) , т. е.
, т. е.
![F (y) = \gamma \sim Rav [0, 1] .](/sites/default/files/tex_cache/08b1cad1c51c0bf4ee04f4323cdc9fda.png)
По определению, 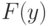 является функцией распределения случайной величины
является функцией распределения случайной величины 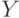 .
.
Теорема может быть проиллюстрирована графиками, представленными на рис. 3.10.
Обозначим: 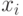 -
-  -е число из
-е число из ![\gamma\sim Rav[0, 1]](/sites/default/files/tex_cache/03878aa0921076af8a3fd50ca0fc011b.png) ,
,  -
-  -е случайное число из произвольного распределения.
-е случайное число из произвольного распределения.

Моделировать равномерно распределенное случайное число 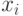 мы уже умеем. Нужно найти неизвестное
мы уже умеем. Нужно найти неизвестное  , находящееся в верхнем пределе интегрирования.
, находящееся в верхнем пределе интегрирования.
Относительно  ыражение принимает вид:
ыражение принимает вид:

Отсюда и название - "метод обратной функции".
Пример 3.6. Получить формулу для моделирования случайных
чисел, распределенных по экспоненциальному закону, с параметром 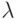 (матожиданием
(матожиданием  ).
).
Плотность 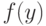 и функция
и функция 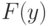 этого распределения имеют вид (рис. 3.11):
этого распределения имеют вид (рис. 3.11):
Решение
![\xi =\int\limits_{-\infty}^{y_i}{f(y)dy}=
\int\limits_{-\infty}^{0}{f(y)dy}+\int\limits_{0}^{y_i}{f(y)dy}=
\int\limits_{0}^{y_i}{f(y)dy}=1-e^{-\lambda y_i}\\
x_i \in Rav[0,1];\,\,
e^{-\lambda y_i}=1-x_i;\,\,
{-\lambda y_i}=\ln{(1-x_i)};\,\,
y_i=-\cfrac{1}{\lambda}{(1-x_i)}](/sites/default/files/tex_cache/5c31b250992f741e62a0edbbb10bef7b.png)
Поскольку случайная величина 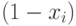 имеет равномерное распределение в интервале
имеет равномерное распределение в интервале ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) , как и
, как и  , то справедливо:
, то справедливо:

Примеров подобного аналитического преобразования случайного числа ![x_{i} \in Rav[0, 1]](/sites/default/files/tex_cache/f95009bf5f22ba31a845c845a9092ccd.png) в случайное число из произвольного распределения немного, так как для многих законов распределения, встречающихся в практике моделирования, интеграл (3.1) относится к неберущимся, а численные методы решения увеличивают затраты машинного времени.
в случайное число из произвольного распределения немного, так как для многих законов распределения, встречающихся в практике моделирования, интеграл (3.1) относится к неберущимся, а численные методы решения увеличивают затраты машинного времени.
Поэтому в современных системах моделирования применяется приближенный метод обратной функции, основанный на кусочно-линейной аппроксимации функции распределения моделируемой случайной величины.
Суть метода заключается в следующем.
Требуемый закон распределения случайной величины размещается в памяти компьютера в виде координат функции распределения. Каждая координата состоит из случайного числа  и соответствующего значения функции распределения
и соответствующего значения функции распределения 

Чем больше координат, тем точнее будет моделирование. Приемлемая точность обеспечивается заданием 20…30 координат.
При обращении за очередным случайным числом нужного закона распределения сначала генерируется случайное число из ![Rav[0,1].](/sites/default/files/tex_cache/56644ec2ab6149a43d37589a509db848.png) Это число сравнивается со значениями
Это число сравнивается со значениями  .
.
При совпадении выдается соответствующее случайное число  .
.
Если нет совпадения, то случайное число  вычисляется из подобия треугольников, как показано на рис. 3.12.
вычисляется из подобия треугольников, как показано на рис. 3.12.
Из подобия треугольников ABC и AB'C' следует:

Отсюда по ![x_{i} \in Rav[0, 1]](/sites/default/files/tex_cache/dd3b832b0727112d2b96191c32b80f9a.png) находится значение
находится значение  .
.
Значительную роль в моделировании играет случайная величина, имеющая нормальное распределение. Метод обратной функции в аналитическом виде здесь неприемлем, так как интеграл (3.1) неберущийся, а его численное решение громоздко.
Для генерации случайных чисел, подчиненных нормальному распределению, применяется метод обратной функции с кусочно-линейной аппроксимацией, а также метод, основанный на центральной предельной теореме (ЦПТ) теории вероятностей.
Как известно, ЦПТ дает теоретическое объяснение подтвержденному практикой наблюдению: если исход случайного события определяется большим числом случайных факторов, и влияние каждого фактора мало, то такой случайный исход хорошо аппроксимируется нормальным распределением. Эта теорема имеет много формулировок. Одна из наиболее практичных для целей моделирования случайных последовательностей - теорема Леви-Линдеберга.
![\eta=\cfrac{\sum\limits_{i=1}^{N}{x_i}-NM[x]}{\sqrt{ND[x]}}](/sites/default/files/tex_cache/62e2d769f715b51ed7560d6cdce770e8.png)
где  - сумма
- сумма  случайных чисел одного и того же распределения с матожиданием
случайных чисел одного и того же распределения с матожиданием ![M[x]](/sites/default/files/tex_cache/b34133f00814d1d8749df12a4aaef591.png) и дисперсией
и дисперсией ![D[x]](/sites/default/files/tex_cache/c936d1d35378167e928da18edac35e49.png) при
при 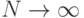 асимптотически стремится к нормальному распределению с
асимптотически стремится к нормальному распределению с ![M[\eta] = 0](/sites/default/files/tex_cache/1eec4df6bfb56e8975396db506e194b8.png) и дисперсией
и дисперсией ![D[\eta] = 1](/sites/default/files/tex_cache/0df1d149a786d07a488ca59030b9fd35.png) .
.
Удобно случайные числа 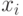 брать из рассмотренного датчика
брать из рассмотренного датчика ![у \sim Rav[0, 1]](/sites/default/files/tex_cache/6c3e4b5755cd55fa6dc159eee90136d5.png) . В этом случае
. В этом случае ![M[\gamma] = \cfrac{1}{2},](/sites/default/files/tex_cache/b295e30ccd23d8b5990c92da78e1c335.png)
![D[\gamma] =\cfrac{1}{12}](/sites/default/files/tex_cache/7e3bdb4ee6d963193fc708f6a8e32d5b.png) .
.
Хорошее приближение к нормальному распределению получается уже при числе  Каждое случайное число при
Каждое случайное число при 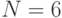 генерируется так:
генерируется так:
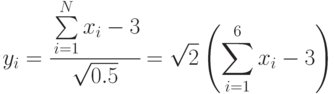
Недостаток способа состоит в том, что он не экономичен, так как для генерирования одного случайного числа  требуется шесть случайных чисел из распределения
требуется шесть случайных чисел из распределения ![у \sim Rav[0, 1]](/sites/default/files/tex_cache/6c3e4b5755cd55fa6dc159eee90136d5.png) .
.
В ряде случаев применяют датчики с числом  . Тогда
. Тогда
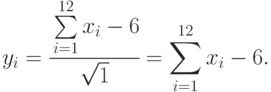
Если датчик случайных чисел нормального распределения выдает стандартную последовательность чисел с 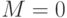 ,
,  , то пересчет на произвольное значение характеристик выполняется так:
, то пересчет на произвольное значение характеристик выполняется так:

где 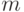 - требуемое значение матожидания;
- требуемое значение матожидания;
 - требуемое значение среднего квадратического отклонения;
- требуемое значение среднего квадратического отклонения;
 - случайное число из нормального распределения с математическим ожиданием
- случайное число из нормального распределения с математическим ожиданием 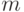 и средним квадратическим отклонением
и средним квадратическим отклонением  .
.
В современных системах моделирования имеются встроенные датчики, позволяющие непосредственного задавать нужную случайную величину с требуемыми значениями характеристик. Однако если исследователя эти возможности не удовлетворяют (например, по точности представления функции распределения вероятностей), то он может задать требуемый закон распределения самостоятельно.
3.6. Моделирование единичного события
Под единичным событием мы будем понимать смену состояний одного элемента (системы), причем состояний всего два: оборудование исправно - неисправно, канал СМО свободен - занят, цель поражена - не поражена и т. п.
Переход из одного состояния в другое - случайный. В любой момент времени система находится в одном состоянии с вероятностью  , в другом - с вероятностью
, в другом - с вероятностью 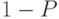 .
.
Цель моделирования: имитировать состояние такого элемента.
Теорема. Пусть некоторое событие  свершается с вероятностью
свершается с вероятностью  . Это может быть отказ техники, поступление сообщения, уничтожение цели и т. п.
. Это может быть отказ техники, поступление сообщения, уничтожение цели и т. п.
Моделью свершения такого единичного события A является попадание значения 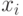 случайной величины
случайной величины  , равномерно распределенной в интервале
, равномерно распределенной в интервале ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) , в числовой интервал
, в числовой интервал ![[0, P(A)]](/sites/default/files/tex_cache/825a9d1d3a4f785371b4eeacfac212de.png) .
.
Доказател ьство Как известно

Для ![x_i\in \gamma \sim Rav[0,1], \, a=0,\, b=P(A)](/sites/default/files/tex_cache/24346e5bd7f5e5bde2570c1e163e8cf0.png)
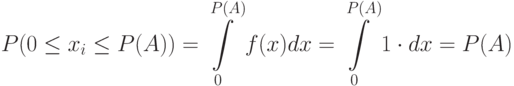
так как 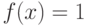 для
для ![\gamma \sim Rav[0,1]](/sites/default/files/tex_cache/1c351711deba35154427ddf86254f507.png) на интервале
на интервале ![[0,P(A)]](/sites/default/files/tex_cache/6779a863d0c720ef7fe6fddd923ec83b.png) .
.
Пример 3.7. Пусть вероятность состояния элемента  В
В 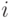 -ой реализации случайное число
-ой реализации случайное число ![x_{i}\in\gamma\sim Rav[0, 1]](/sites/default/files/tex_cache/5c65b565a66309b795fe1b369c7f9d96.png) равно
равно  Это означает, что в данной
Это означает, что в данной  -ой реализации модели событие A не свершилось (рис. 3.13). Естественно, одна реализация ни о чем не говорит. Реальная ситуация будет отображена на множестве реализаций и чем их больше, тем точнее.
-ой реализации модели событие A не свершилось (рис. 3.13). Естественно, одна реализация ни о чем не говорит. Реальная ситуация будет отображена на множестве реализаций и чем их больше, тем точнее.
Фрагмент алгоритма имитации в модели единичного случайного события приведен на рис. 3.14.