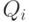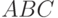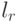| Высшее образование |
Статистическое моделирование
3.9. Моделирование совместных зависимых событий
Пусть события A и B имеют вероятности свершения 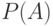 и
и 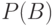 соответственно. Условная вероятность
соответственно. Условная вероятность  известна.
известна.
Покажем способ моделирования совместных зависимых событий на примере.
Пример 3.9. При испытании нового автомата определены вероятности горизонтального и вертикального отклонений пробоин от точки прицеливания  и
и 
Вероятность отклонения пробоин по высоте относительно тех, которые уложились в пределы допустимого бокового отклонения, равна:

Соответствующий фрагмент модели приведен на рис. 3.18.
Пример 3.10. В ремонтное подразделение поступают вышедшие из строя средства связи (СС). В каждом СС могут быть неисправными в любом сочетании блоки A, B, C . Вероятности выхода из строя блоков  ,
,  ,
,  соответственно. Ремонт производится путем замены неисправных блоков исправными блоками. В момент поступления неисправного СС вероятности наличия исправных блоков
соответственно. Ремонт производится путем замены неисправных блоков исправными блоками. В момент поступления неисправного СС вероятности наличия исправных блоков  ,
,  ,
,  соответственно. При отсутствии хотя бы одного из исправных блоков A, B, C ремонт неисправного СС не производится.
соответственно. При отсутствии хотя бы одного из исправных блоков A, B, C ремонт неисправного СС не производится.
Построить алгоритм имитационной модели с целью определения абсолютного и относительного количества отремонтированных СС с неисправными блоками A, B, C и A, B из общего количества R поступивших в ремонт СС.
Решение
Для имитации неисправных блоков СС и имитации наличия исправных блоков в ремонтном подразделении воспользуемся способом определения по жребию. Для этого рассчитаем вероятности исходов и сведем их в табл. 3.5 и 3.6 соответственно.
Так как нужно определить абсолютное и относительное количества отремонтированных СС, поступивших с неисправными блоками A, B и A, B, C , то нет смысла рассчитывать вероятности для других сочетаний неисправных и исправных блоков.
Алгоритм имитационной модели приведен на рис. 3.19.
В алгоритме приняты следующие обозначения:
 - заданное количество реализаций модели;
- заданное количество реализаций модели;
 - счетчик количества реализаций модели;
- счетчик количества реализаций модели; 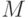 - счетчик числа отремонтированных СС за
- счетчик числа отремонтированных СС за  реализаций модели;
реализаций модели;
 - абсолютное количество отремонтированных СС;
- абсолютное количество отремонтированных СС;
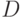 - относительное количество отремонтированных СС.
- относительное количество отремонтированных СС.
Согласно постановке задачи в блоках 3…7 по данным табл. 3.5 разыгрывается, с какими неисправными блоками поступает СС в ремонт. В результате розыгрыша определяется номер интервала (столбца табл. 3.5) и запоминается в переменной  .
.
Аналогично в блоках 8…11 разыгрывается по данным табл. 3.6 наличие в ремонтном подразделении необходимых блоков для замены.
Если такие блоки имеются, т. е. выполняется условие  в блоке 12, в счетчик
в блоке 12, в счетчик 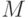 (блок 13) добавляется единица.
(блок 13) добавляется единица.
3.10. Классификация случайных процессов
Случайная величина  зависящая от одного неслучайного вещественного аргумента
зависящая от одного неслучайного вещественного аргумента  , называется случайным процессом.
, называется случайным процессом.  является случайной величиной при каждом фиксированном
является случайной величиной при каждом фиксированном
значении аргумента. Обычно (во всяком случае, для процессов, протекающих в технических системах) в качестве вещественного аргумента выступает время, поэтому случайный процесс будем обозначать  .
.
Определим два понятия, присущие случайным процессам: сечение и реализация (рис. 3.20).
Сечением случайного процесса  называется случайная величина
называется случайная величина  являющаяся значением случайного процесса в фиксированный момент времени
являющаяся значением случайного процесса в фиксированный момент времени 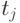 .
.
Реализацией случайного процесса  называется функция времени
называется функция времени  описывающая течение процесса в некотором
описывающая течение процесса в некотором 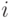 -м опыте.
-м опыте.
Случайный процесс  и аргумент
и аргумент  могут быть дискретными или непрерывными.
могут быть дискретными или непрерывными.
Очевидно, вследствие особенностей представления информации в компьютере моделью случайного процесса будет модель дискретной последовательности дискретного случайного процесса. Следовательно, чтобы смоделировать реальный случайный процесс, необходимо выполнить следующее:
- разбить интервал исследования на M временных точек
 , которых должно быть столько, чтобы обеспечить необходимую точность воспроизведения исследуемого процесса;
, которых должно быть столько, чтобы обеспечить необходимую точность воспроизведения исследуемого процесса; - выполнить одну реализацию случайного процесса, то есть для каждого момента времени
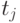 определить сечение, разыграв случайное число, обладающее характеристиками случайного процесса;
определить сечение, разыграв случайное число, обладающее характеристиками случайного процесса; - определить аналогичные сечения для каждой из
 реализаций случайного процесса (число
реализаций случайного процесса (число  выбирается таким, чтобы обеспечить необходимые точность и достоверность результатов).
выбирается таким, чтобы обеспечить необходимые точность и достоверность результатов).
Случайные процессы могут быть:
- стационарные;
- нестационарные.
На практике часто встречаются случайные процессы, у которых все реализации однородны в вероятностном смысле. То есть значения всех сечений представляют собой случайные числа, одинаково распределенные с одинаковыми матожиданиями и дисперсиями:
![M[x(t)]=M[x];\,\, D[x(t)] = D[x].](/sites/default/files/tex_cache/94a86d9bdc0f08b315067253b61df053.png)
Такие процессы называют стационарными.
Что касается автокорреляционной функции  , то ее значение в стационарном процессе зависит только от разности
, то ее значение в стационарном процессе зависит только от разности  и не зависит от того, в каком месте временной оси находятся точки
и не зависит от того, в каком месте временной оси находятся точки 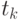 и
и 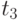 .
.
Для стационарного процесса нет необходимости определять искомые характеристики для всех 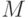 сечений, а достаточно только для одного сечения
сечений, а достаточно только для одного сечения  реализаций случайного процесса. То есть вместо
реализаций случайного процесса. То есть вместо  измерений выполнить только
измерений выполнить только  измерений. По данным этих измерений рассчитываются оценки
измерений. По данным этих измерений рассчитываются оценки  и
и  , которые в силу стационарности и являются оценками характеристик всего случайного процесса
, которые в силу стационарности и являются оценками характеристик всего случайного процесса ![M[x]](/sites/default/files/tex_cache/b34133f00814d1d8749df12a4aaef591.png) и
и ![D[x]](/sites/default/files/tex_cache/c936d1d35378167e928da18edac35e49.png) .
.
Если сечения случайного процесса неоднородны в вероятностном смысле, то такой процесс называется нестационарным.
В работе модели стационарного процесса может присутствовать и нестационарный период. Это разного рода переходные процессы. Например, характеристики начального периода работы модели нестационарные из-за того, что начальные установки характеристик процесса были не равны характеристикам, значения которых установятся в дальнейшем. Естественно, речь идет о средних значениях характеристик.
Важнейшим свойством случайного процесса является свойство эргодичности.
Свойство эргодичности заключается в том, что все реализации случайного процесса имеют одинаковые статистические характеристики. Отсюда следует, что одна реализация случайного процесса характеризует весь случайный процесс  следовательно, для определения статистических характеристик процесса достаточно выполнить одну реализацию.
следовательно, для определения статистических характеристик процесса достаточно выполнить одну реализацию.
Обычно рассматривают свойство эргодичности по отношению к одной какой-либо характеристике случайного процесса. Относительно оценки матожидания свойство эргодичности формально выглядит так:

Свойством эргодичностиобладают многие случайные процессы и, в том числе, все стационарные.
Таким образом, можно сформулировать определение эргодиче-ского процесса.
Случайный процесс  называется эргодическим, если его основные характеристики
называется эргодическим, если его основные характеристики ![M [x]](/sites/default/files/tex_cache/6663ef7e91d107e10c13db7983032d7d.png) и
и ![D[x]](/sites/default/files/tex_cache/c936d1d35378167e928da18edac35e49.png) могут быть получены не только усреднением по множеству реализаций, но и усреднением по времени одной реализации.
могут быть получены не только усреднением по множеству реализаций, но и усреднением по времени одной реализации.
Например, при изучении флуктуационного шума радиоприемников, представляющего собой стационарный случайный процесс, достаточно ограничиться измерением сечений в течение заданного времени 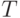 в одном конкретном образце. Результаты, полученные при обработке данных измерений, могут быть распространены на все идентичные радиоприемники.
в одном конкретном образце. Результаты, полученные при обработке данных измерений, могут быть распространены на все идентичные радиоприемники.