| Высшее образование |
Статистическое моделирование
Имитационная модель представляет собой программу, реализованную на компьютере, описывающую (моделирующую) функционирование элементов моделируемой системы, их связь между собой и внешней средой. Поэтому имитационную модель следует называть компьютерной моделью и имитационное моделирование - компьютерным моделированием, тем более, что название "имитационное моделирование" несет в себе тавтологию: имитация и моделирование - очень сходные понятия. Тем не менее, термин "имитационное моделирование" прижился и широко используется в отечественной технической и научной литературе.
Имитационная модель является функциональной, так как она создается для получения характеристик моделируемого процесса, а не структуры. Однако, моделирующий алгоритм, как правило, имеет модульную структуру, аналогичную размещению и связям элементов в моделируемом объекте.
Имитационная модель дает численное решение задачи, что не позволяет непосредственно усматривать функциональные связи между параметрами процесса, как это демонстрируют аналитические модели. Однако, выполнив серию экспериментов с моделью, направленно изменяя значения исследуемого фактора, и, выполнив обработку результатов, можно построить искомую связь между показателем эффективности системы и исследуемым фактором.
Имитационную модель, в отличие от аналитической модели, можно разработать с любой детализацией процесса или явления.
Как правило, имитационные модели создают для исследования процессов, на течение которых влияют различного рода случайности: отказы и сбои технических устройств, неточности измерений, рассеивание попаданий относительно точек прицеливания, и многое другое. Следовательно, результат такого процесса случаен. В имитационной модели случайные факторы моделируются при помощи специально подобранных генераторов случайных величин, которые входят в современные системы имитационного моделирования. Для получения характеристик таких вероятностных операций имитационная модель многократно реализуется на компьютере. Полученный при этом ряд значений исследуемого параметра подвергается статистической обработке, в результате которой и определяются характеристики случайных показателей процесса - матожидание, дисперсия, закон распределения и т. п. Такие имитационные модели называют статистическими имитационными или статистическими.
3.1. Сущность имитационного моделирования
Сущность имитационного моделирования рассмотрим на примере.
Пример 3.1. По объекту наносится одиночный ракетный удар. Радиус поражения  .
.
Попадание ракеты в цель характеризуется рассеиванием, распределенным по нормальному закону со среднеквадратическими отклонениями:
- по дальности
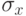 ;
; - по направлению
 .
.
Цель будет уничтожена, если расстояние 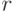 от нее (то есть от точки прицеливания) до центра взрыва ракеты будет меньше или равно
от нее (то есть от точки прицеливания) до центра взрыва ракеты будет меньше или равно  , то есть
, то есть 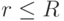 .Так как
.Так как  размеров объекта, то цель можно считать точечной.
размеров объекта, то цель можно считать точечной.
Наличие рассеивания исключает однозначный ответ: "цель поражена - цель не поражена". Задача носит вероятностный характер, поэтому в результате моделирования может быть получен ответ: цель будет поражена с вероятностью 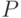 .
.
Цель моделирования: определить вероятность 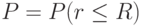 поражения объекта одиночным ракетным ударом.
поражения объекта одиночным ракетным ударом.
Решение
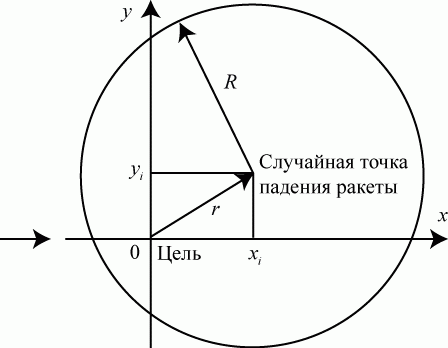
Построим декартову систему координат так, чтобы точечный объект находился в начале координат, а направление пуска ракеты совпадало с осью 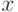 (рис. 3.1).
(рис. 3.1).
Возьмем две последовательности нормально распределенных случайных чисел:
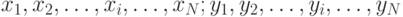
Первая последовательность соответствует распределению ![М[х] = 0, \sigma_{Х} = a](/sites/default/files/tex_cache/ce0ebf9455d7363638cbe4cc7307141d.png) , вторая -
, вторая - ![М[у] = 0, \sigma_y = b](/sites/default/files/tex_cache/e79ad808ab53791bbdd51c9fdb41040b.png) . Матожидания
. Матожидания ![M[x]](/sites/default/files/tex_cache/b34133f00814d1d8749df12a4aaef591.png) ,
,
![М[у]](/sites/default/files/tex_cache/ae14cd52c36d68c52b380cd60abc351e.png) взяты равными нулю, так как объект поражения (точка прицеливания) находится в начале координат, то есть имеет координаты
взяты равными нулю, так как объект поражения (точка прицеливания) находится в начале координат, то есть имеет координаты 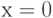 и
и 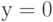 .
.
Закон и характеристики случайных чисел  и
и  соответствуют закону рассеивания пуска ракет.
соответствуют закону рассеивания пуска ракет.
Моделирование
- Имитируем удар, то есть мысленно нанесем удар по объекту путем определения координат взрыва. В силу идентичности закона рассеивания и его характеристик с законами распределения случайных чисел такими координатами могут быть
 и
и 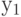 , взятые из последовательностей случайных чисел.
, взятые из последовательностей случайных чисел. - Вычислим расстояние
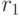 от места взрыва ракеты до цели:
от места взрыва ракеты до цели: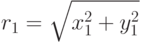
- Оценим результаты имитации удара, то есть установим факт поражения или непоражения объекта:
- если
 , то объект поражен;
, то объект поражен; - если
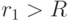 , то объект непоражен.
, то объект непоражен.
- если
- Если объект поражен, запомним этот факт увеличением
 на единицу, то есть
на единицу, то есть 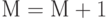 (в начале
(в начале  ).
). - Для нахождения вероятности поражения объекта повторим имитацию нанесения удара
 раз.
раз. - Оценим вероятность через частость поражения объекта:
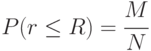
Возможность оценки вероятности частостью доказывается теоремой Я. Бернулли: при неограниченном числе однородных независимых опытов с практической достоверностью можно утверждать, что частота события будет сколь угодно мало отличаться от его вероятности в отдельном опыте (Бернулли Якоб 1 - самый старший из восьми представителей этой швейцарской семьи - выдающихся ученых).
Чем больше число  (число реализаций, число испытаний, число прогонов модели), тем точнее будет оценка вероятности
(число реализаций, число испытаний, число прогонов модели), тем точнее будет оценка вероятности 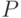 .
.
В рассмотренном примере 3.1 при 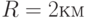 ,
, 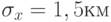 ,
,  оценки вероятностей
оценки вероятностей 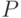 поражения цели при различном числе реализаций модели показаны в табл. 3.1.
поражения цели при различном числе реализаций модели показаны в табл. 3.1.
При  , тех же характеристиках рассеивания и других радиусах поражения
, тех же характеристиках рассеивания и других радиусах поражения 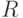 получим:
получим:
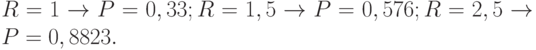
В одной из последующих тем мы установим количественную связь между числом реализаций модели  , требуемой точностью и доверительной вероятностью результата моделирования, в данном случае оценки вероятности
, требуемой точностью и доверительной вероятностью результата моделирования, в данном случае оценки вероятности 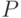 .
.
Данный пример иллюстрирует сущность метода имитационного моделирования , который заключается в следующем.
- Создается модель, поведение которой подчиняется тем же вероятностным законам, что и интересующий нас процесс.
- По известным законам распределения для отдельных характеристик процесса выбираются их случайные значения.
- Вычисляются параметры исхода процесса при случайных значениях характеристик, полученных на этапе 2, и запоминаются. Этапы 2 и 3 соответствуют одному статистическому испытанию.
- В результате
 статистических испытаний (повторений этапов 2 и 3) получают
статистических испытаний (повторений этапов 2 и 3) получают  значений параметров исхода процесса. Вероятностные характеристики параметров исхода процесса получают в результате статистической обработки полученных случайных величин.
значений параметров исхода процесса. Вероятностные характеристики параметров исхода процесса получают в результате статистической обработки полученных случайных величин.
Статистическая обработка и оценка точности результатов моделирования основываются на предельных теоремах теории вероятностей: теореме Чебышева и теореме Бернулли.
Рассмотрим еще один пример.
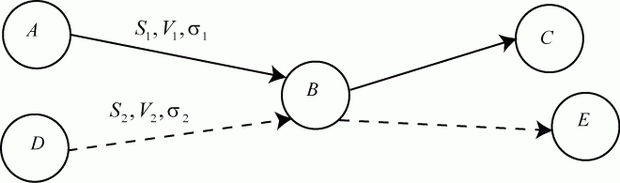
Пример 3.2. Транспорт 1 с грузом отправился из пункта А в пункт С через пункт В. Одновременно из пункта D в пункт Е через пункт В отправился транспорт 2. Скорости движения транспортов распределены по нормальному закону с математическими ожиданиями 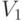 и
и 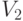 и стандартными отклонениями
и стандартными отклонениями 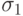 и
и 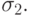
Построить алгоритм имитационной модели (ИМ) с целью определения вероятности встречи транспортов 1 и 2 в пункте В. Расстояние от пункта А до пункта В 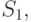 а от пункта D до пункта В -
а от пункта D до пункта В - 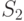 .Событие встречи считать состоявшимся, если их времена прибытия в пункт В либо равны, либо отличаются на величину, не превышающую
.Событие встречи считать состоявшимся, если их времена прибытия в пункт В либо равны, либо отличаются на величину, не превышающую  .
.
Решение
Построим схему движения транспортов 1 и 2 (рис. 3.2).
Возьмем две последовательности нормально распределенных случайных чисел:
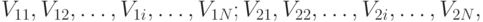
характеристики которых соответствуют матожиданиям и стандартным отклонениям скоростей движения транспортов 1 и 2.
- Имитируем движение транспортов 1 и 2 до пункта В со скоростями
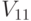 и
и 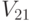 соответственно, взятыми из последовательностей нормально распределенных случайных чисел.
соответственно, взятыми из последовательностей нормально распределенных случайных чисел. - Вычислим время
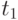 и
и 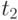 прибытия в пункт В транспортов 1 и 2 соответственно:
прибытия в пункт В транспортов 1 и 2 соответственно:
- Оценим результат имитации движения транспортов 1 и 2, т. е. установим факт наличия или отсутствия их встречи:
- если
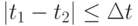 , встреча состоялась;
, встреча состоялась; - если
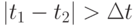 , встреча не состоялась.
, встреча не состоялась.
- если
- Если встреча состоялась, зафиксируем этот факт увеличением значения
 на
на  , т. е.
, т. е. 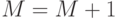 (вначале
(вначале 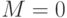 ).
). - Для нахождения вероятности встречи транспортов 1 и 2 повторим имитацию их движения
 раз.
раз.
Рассчитаем вероятность встречи:
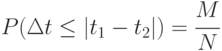
Результаты моделирования при 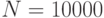 и характеристиках движения транспортов:
и характеристиках движения транспортов: 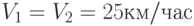 ,
, 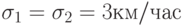 ,
,  :
:

Очевидно, изложенный процесс имитации легко может быть реализован на компьютере. Представим алгоритмы моделей примеров 3.1 и 3.2 схемами (рис. 3.3 и 3.4).
В рассмотренных примерах исследуются различные процессы. Но алгоритмы моделей этих процессов (для сравнения рядом с алгоритмом задачи 3.2 (рис. 3.3) показан и алгоритм задачи 3.1 (рис. 3.4) имеют общую, практически идентичную часть (блоки 1, 5…8, на рис. 3.3 и 3.4 они выделены) и часть, которая непосредственно имитирует исследуемый процесс (блоки 2… 4).
Подобное сходство и различие еще раз подтверждают сформулированную нами ранее сущность имитационного моделирования.
Пример 3.3. По объекту наносится не одиночный, а три последовательных ракетных удара. При поражении объекта любой ракетой пуски прекращаются. Остальные условия те же, что и в примере 3.1.
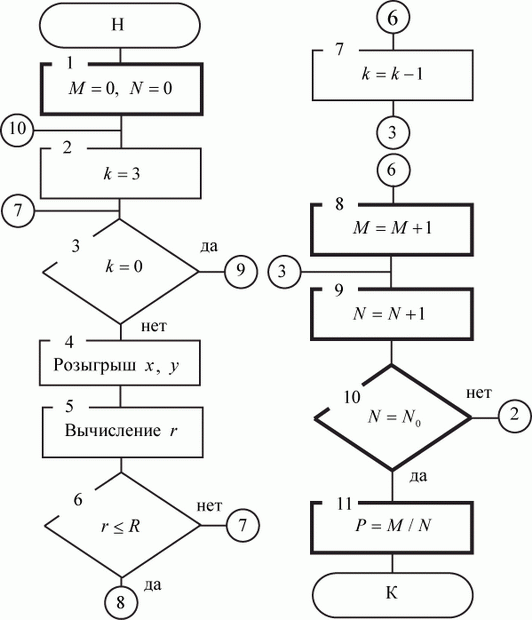
Алгоритм ИМ приведен на рис. 3.5. На нем выделены блоки 1, 8…11, выполняющие те же функции, что блоки 1, 5…8 в алгоритмах ИМ на рис. 3.3 и 3.4. Блоки 2…7 непосредственно имитируют нанесение удара по объекту, т. е. выполняют одну реализацию (один прогон модели). В блоке 2 переменной  присваивается начальное число пусков ракет. Далее эта переменная используется для организации внутреннего цикла по числу пусков. После каждого пуска значение k уменьшается на 1 (блок 7). При
присваивается начальное число пусков ракет. Далее эта переменная используется для организации внутреннего цикла по числу пусков. После каждого пуска значение k уменьшается на 1 (блок 7). При 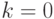 (блок 3) реализация завершается. Завершается она также и при поражении объекта (блок 6). Но при этом предварительно значение переменной
(блок 3) реализация завершается. Завершается она также и при поражении объекта (блок 6). Но при этом предварительно значение переменной  увеличивается на
увеличивается на  . По завершении
. По завершении 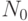 реализаций рассчитывается оценка математического ожидания вероятности поражения объекта тремя последовательными пусками ракет.
реализаций рассчитывается оценка математического ожидания вероятности поражения объекта тремя последовательными пусками ракет.
Как отмечалось вначале, название метода - имитационное моделирование не очень удачно в том смысле, что несет в себе тавтологию: моделирование и есть имитация. Однако название прижилось. Очень часто метод называют статистическим моделированием из-за необходимости статистической обработки накапливаемого результата - в случае вероятностных операций.
Иногда статистическое моделирование называют "метод Монте-Карло", по городу, где процветает игра в рулетку, исход которой случаен и образуется своеобразным датчиком случайных исходов - рулеткой.