| Высшее образование |
Статистическое моделирование
3.7. Моделирование полной группы несовместных событий
Элемент системы (или система в целом) может находиться во многих (больше двух) несовместных состояниях. Известны вероятности нахождения системы в этих состояниях. Например, средство вооружения может находиться:
- в боеготовом состоянии с вероятностью
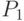 ;
; - в неисправном состоянии и ремонтироваться силами своего расчета, вероятность этого состояния
 ;
; - ремонтироваться в мастерской части -
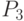 ;
; - ремонтироваться на заводе -
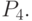 Очевидно, что
Очевидно, что 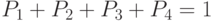 .
.
Такие и аналогичные события называются полной группой несовместных событий.
Алгоритм моделирования основан на следующей теореме.
Теорема. В полной группе несовместных событий моделью свершения события 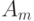 , происходящего с вероятностью
, происходящего с вероятностью 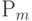 , является попадание значения
, является попадание значения ![х_i\in\gamma \sim Rav[0, 1]](/sites/default/files/tex_cache/580284b65d0b8e74ae36f23ea175d524.png) в отрезок, равный
в отрезок, равный 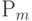 , числовой шкалы
, числовой шкалы 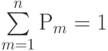 , где
, где  - число несовместных событий (рис. 3.15):
- число несовместных событий (рис. 3.15):
Доказател ьство
Введем численные обозначения концов отрезков 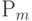 по нарастанию:
по нарастанию:
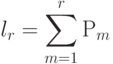
В этом случае, согласно теореме, условием свершения события 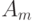 является:
является:
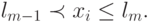
Следовательно
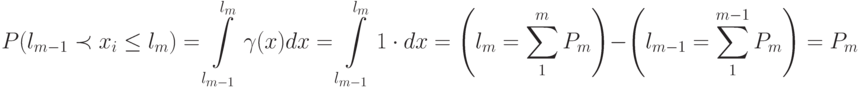
Такой способ моделирования несовместных событий обычно называют определением исходов по жребию.
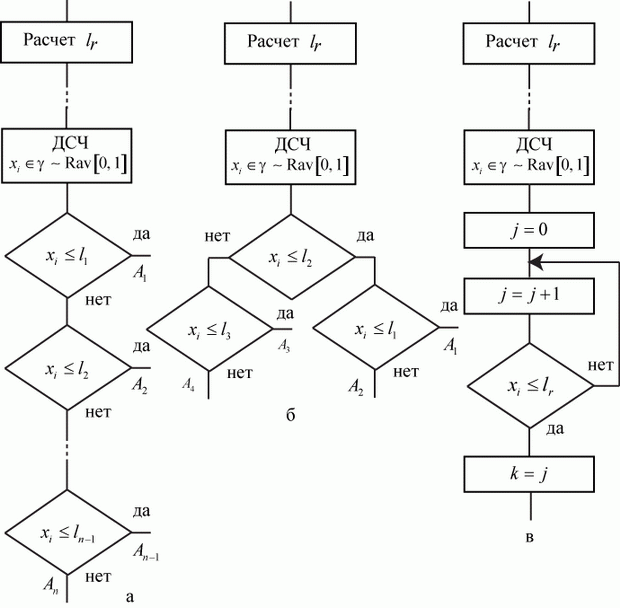
Алгоритм, реализующий способ определения исходов по жребию, может быть построен тремя вариантами, представленными на рис. 3.16.
Первый вариант (рис. 3.16а) применяется тогда, когда число возможных исходов невелико и не равно степени по основанию два.
На рис. 3.16б алгоритм построен по способу половинных сечений для четырех исходов.
Третий вариант алгоритма (рис. 3.16в) в цикле определяет исход (событие), номер которого присваивается переменной  . Далее этот номер используется для организации нужной работы алгоритма. Применение данного алгоритма будет показано в главе 6 (п. 6.7 и п. 6.8).
. Далее этот номер используется для организации нужной работы алгоритма. Применение данного алгоритма будет показано в главе 6 (п. 6.7 и п. 6.8).
Пример 3.8. Канал передачи данных может находиться в одном из четырех несовместных состояниях:
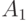 - исправен и свободен,
- исправен и свободен, 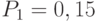 ;
;
 - исправен и занят,
- исправен и занят,  ;
;
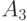 - неисправен,
- неисправен, 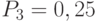 ;
;
 - подавлен помехами,
- подавлен помехами, 
Решение
Представим необходимые для определения исходов по жребию данные табл. 3.3.
| Вероятности | Событие | |||
|---|---|---|---|---|
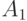 |
 |
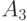 |
 |
|
| Вероятности событий | 0,15 | 0,4 | 0,25 | 0,2 |
Суммарные вероятности ( 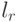 ) ) |
0,15 | 0,55 | 0,8 | 1,0 |
Номера интервалов (  ) ) |
1 | 2 | 3 | 4 |
Предположим, что при выполнении  -ой реализации датчик равномерно распределенных случайных чисел
-ой реализации датчик равномерно распределенных случайных чисел ![\gamma\sim Rav[0, 1]](/sites/default/files/tex_cache/03878aa0921076af8a3fd50ca0fc011b.png) сгенерировал
сгенерировал 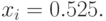 Путем последовательных сравнений определяется, что
Путем последовательных сравнений определяется, что 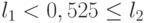 . Значит в данной реализации канал находится в состоянии
. Значит в данной реализации канал находится в состоянии 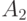 - исправен и занят.
- исправен и занят.
3.8. Моделирование совместных независимых событий
Рассмотрим моделирование совместных независимых событий.
Способ моделирования состоит в том, что совместные независимые события сводятся к одному сложному событию.
Для лучшего понимания и обозримости способа рассмотрим моделирование двух событий A и B. Увеличение числа событий ничего принципиально нового в моделирование не вносит.
Пусть независимые события A и B происходят с вероятностями 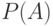 и
и 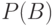 соответственно. Например, это могут быть отказы монитора и процессора компьютера.
соответственно. Например, это могут быть отказы монитора и процессора компьютера.
Моделирование такой ситуации может быть выполнено двумя способами:
- определение совместных исходов выбором по жребию;
- последовательная проверка исходов.
3.8.1. Определение совместных исходов по жребию
Прежде всего, по вероятностям 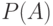 и
и 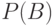 нужно определить вероятности возможных исходов, т. е. появления совместных независимых событий. Возможные исходы совместного события
нужно определить вероятности возможных исходов, т. е. появления совместных независимых событий. Возможные исходы совместного события 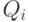 и соответствующие вероятности
и соответствующие вероятности 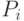 представлены в табл. 3.4.
представлены в табл. 3.4.
Совместное событие в 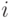 -ой реализации определяется выбором исхода по жребию.
-ой реализации определяется выбором исхода по жребию.
Если случайное число ![x_{i} \in \gamma \sim Rav[0, 1]](/sites/default/files/tex_cache/8a7b82e2cc806dc8ea60426d85a9aa66.png) при очередной реализации окажется, например, на участке
при очередной реализации окажется, например, на участке 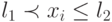 , то в данной реализации фиксируется свершение сложного события
, то в данной реализации фиксируется свершение сложного события  . Если же окажется
. Если же окажется 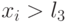 , то фиксируется событие
, то фиксируется событие  . Алгоритм может быть построен по одному из приведенных на рис. 3.16 вариантов.
. Алгоритм может быть построен по одному из приведенных на рис. 3.16 вариантов.
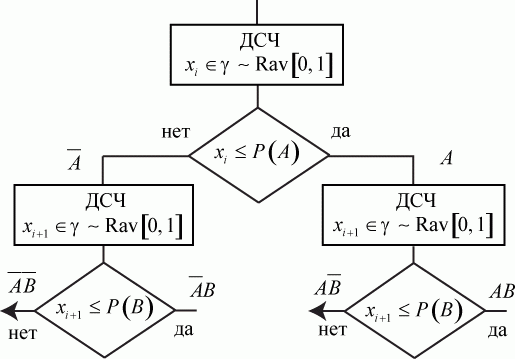
3.8.2. Последовательная проверка исходов
Алгоритм способа последовательной проверки исходов приведен на рис. 3.17.
Проверку свершения каждого из совместных событий надо осуществлять разными случайными числами, так как события независимые. При первом способе достаточно одного случайного числа  , но сравнений может быть больше. Кроме того, нужно предварительно рассчитывать вероятности возможных исходов.
, но сравнений может быть больше. Кроме того, нужно предварительно рассчитывать вероятности возможных исходов.

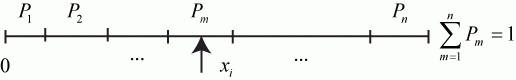
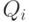
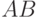




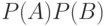
![[1-P(A)]P(B)](/sites/default/files/tex_cache/3eb45c9f6336a1aec70c89003db9568a.png)
![P(A) [1-P(B)]](/sites/default/files/tex_cache/76471baab17c8d5756b4530a1dc39b8e.png)
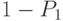
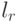
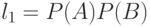
![l_2= l_1+[1-P(A)]P(B)](/sites/default/files/tex_cache/bdaa2714bb5eba86bf950ed69f995ea8.png)
![l_3=l_2+ P(A) [1-P(B)]](/sites/default/files/tex_cache/339360e97138090fcb3e5ef398a69644.png)