НОУ ИНТУИТ | Исследование операций и модели экономического поведения. Лекция 16: Дележ, отвечающий аксиомам Нэша

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.04.2007 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 24 студентам

| Поделиться |

Поддержать

| Скачать электронную книгу

Замечание 3.3 (о графическом определении точки $(u^\circ, v^\circ)$ , доставляющей максимум функции g ). Согласно (15.9), (15.10), уравнение опорной прямой можно представить в виде

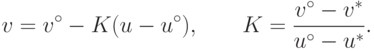$v = v^\circ - K(u - u^\circ),\qquad K = \frac{v^\circ - v^\ast}{u^\circ - u^\ast}.$

( 15.12)

При этом уравнение прямой

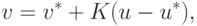$v = v^\ast + K(u - u^\ast),$

( 15.13)

проходящей через точки (u^*,v^*) и $(u^\circ, v^\circ)$ , характеризуется тем же коэффициентом K, что и в (15.12) Таким образом, прямые линии (15.12) и (15.13) пересекаются в точке $(u^\circ, v^\circ)$ . Кроме того, они образуют равные (по абсолютной величине) и противоположные (по знаку) углы с вертикалью, опущенной из этой точки (в качестве иллюстрации см. рис. 3.3). Отмеченное соотношение углов может быть использовано для графического определения точки $(u^\circ, v^\circ)$ , соответствующей задаче (S,u^*,v^*).

Лемма 3.3. При выполнении условий (15.2) точка $(u^\circ, v^\circ)$ из (15.5) удовлетворяет всем аксиомам Нэша.

Доказательство Выполнение условий (14.15) и (14.16) является следствием определения (15.5). Допустим, что в множестве S существует точка (u',v'), доминирующая (т.е. улучшающая) отличную от нее точку $(u^\circ, v^\circ)$ . Тогда должно выполняться неравенство

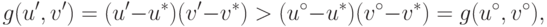
$g(u',v') = (u' - u^\ast)(v' - v^\ast) > (u^\circ - u^\ast) (v^\circ - v^\ast) = g(u^\circ, v^\circ),$

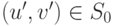противоречащее определению (15.5). Заметим, что из сделанного допущения $(u', v') \ge (u^\circ, v^\circ)$ вытекает включение $(u', v') \in S_0$ . Т.е. аксиома (14.17) также должна выполняться.

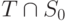Если $(u^\circ, v^\circ) \in T \subset S$ , то максимум функции g(u,v) на множестве $T \cap S_0$ достигается в той же точке, что и на множестве S₀. Т.е. пара $(u^\circ, v^\circ)$ из определения (15.5) удовлетворяет условию (14.19).

Проверим выполнение пятой аксиомы. Согласно (14.20) и (15.3),

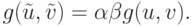$g(\tilde{u},\tilde{v}) = \alpha \beta g(u,v).$

( 15.14)

Теперь из (15.5) и (15.14) вытекает, что

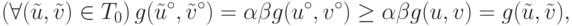
$(\forall (\tilde{u}, \tilde{v}) \in T_0)\, g(\tilde{u}^\circ, \tilde{v}^\circ) =\alpha \beta g(u^\circ, v^\circ) \ge \alpha \beta g(u,v) = g(\tilde{u}, \tilde{v}),$

где T₀ есть образ S₀ при соответствии (14.20). Следовательно,

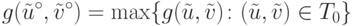
$g(\tilde{u}^\circ, \tilde{v}^\circ) = \max\{g(\tilde{u}, \tilde{v})\colon (\tilde{u}, \tilde{v}) \in T_0\}$

и справедливость (14.21) установлена.

Пусть множество S симметрично, т.е. из включения 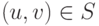$(u, v)\in S$ следует включение 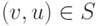$(v, u) \in S$ , и пусть u^*=v^*. Тогда

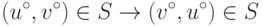
$(u^\circ, v^\circ) \in S \to (v^\circ, u^\circ) \in S$

и

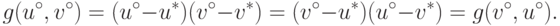
$g(u^\circ, v^\circ) = (u^\circ - u^\ast)(v^\circ - v^\ast) = (v^\circ - u^\ast)(u^\circ - v^\ast) = g(v^\circ, u^\circ).$

Теперь из единственности точки максимума вытекают следствия

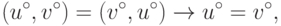
$(u^\circ, v^\circ) = (v^\circ, u^\circ) \to u^\circ = v^\circ,$

доказывающие справедливость аксиомы (14.22).

Лемма 3.4. При выполнении условий (15.2) точка $(u^\circ, v^\circ)$ из (15.5) есть единственная сделка, удовлетворяющая аксиомам Нэша.

Доказательство Определим множество

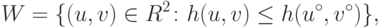
$W = \{(u,v) \in R^2\colon h(u,v) \le h(u^\circ, v^\circ)\},$

лежащее под опорной к нему прямой (15.9) и содержащее допустимое множество S (см. рис. 3.4). Введем линейное преобразование

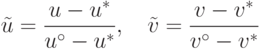$\tilde{u} = \frac{u - u^\ast}{u^\circ - u^\ast}, \quad \tilde{v} = \frac{v - v^\ast}{v^\circ - v^\ast}$

( 15.15)

и определим множество T, являющееся образом W относительно преобразования (15.15).

Рис. 3.4.

Дальше >>

Исследование операций и модели экономического поведения

Дележ, отвечающий аксиомам Нэша

Вопросы и ответы

Студенты

Авторизоваться

Исследование операций и модели экономического поведения

Дележ, отвечающий аксиомам Нэша

Вопросы и ответы

Студенты