| ВКР |
Проверка простой гипотезы относительно простой альтернативы
Байесовское решение как проверка по отношению правдоподобия
Рассмотрим статистическую игру (17.17) при m=n=2. Примером операции такого рода является обсуждавшаяся в "Выбор решений при неизвестных состояниях природы (игры с природой)" задача диагностики туберкулеза. Будем использовать эту задачу для иллюстрации основных положений, вводимых ниже.
Примем, что функция потерь  включает лишь затраты,
вызываемые ошибками при постановке диагноза. При этом потери L(1,2),
связанные с ошибочным направлением на лечение здорового
человека, примем за единицу потерь. Тогда
включает лишь затраты,
вызываемые ошибками при постановке диагноза. При этом потери L(1,2),
связанные с ошибочным направлением на лечение здорового
человека, примем за единицу потерь. Тогда
 |
( 18.1) |
 полностью
определяется заданием единственного числа w>0.
полностью
определяется заданием единственного числа w>0.В соответствии с замечанием о простых гипотезах (см. "Выбор решений при неизвестных состояниях природы (игры с природой)" ), любая статистическая игра с функцией потерь вида (18.1) может интерпретироваться как выбор одной из двух простых гипотез. При этом остающаяся альтернатива также соответствует простой гипотезе.
Отметим, что два типа ошибок статистика, возможных в обсуждавшейся задаче диагностики туберкулеза, вообще говоря, не являются одинаковыми по сопровождающим их потерям. Случай, когда обследование не выявило факт заболевания, следствием чего будет позднее начало лечения запущенной формы болезни, должен рассматриваться как более серьезная ошибка, чем направление здорового человека для прохождения курса лечения1Заметим, что такое направление предполагает более подробное обследование, предшествующее лечению. Затраты на это обследование и ущерб от временного прерывания нормальной жизнедеятельности пациента (не нуждавшегося в лечении) составляют содержание потерь, вызываемых обсуждаемым ошибочным диагнозом..
В задачах выбора решений, для которых характерно указанное различие последствий, вызываемых ошибками, бoлее серьезную ошибку, ведущую к большим потерям, принято называть ошибкой первого рода. Вторая возможная ошибка называется ошибкой второго рода.
Указанное различие в классификации ошибок ведет к соответствующему
различению двух рассматриваемых гипотез. Если отвержение гипотезы,
являющейся истинной, ведет к ошибке первого рода, то ее называют испытуемой гипотезой или нуль-гипотезой.
В рассматриваемом примере диагностики туберкулеза такой гипотезой является
наличие заболевания (т.е. факт порождения исхода испытания 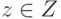 случайной величиной с распределением p2(z) ).
случайной величиной с распределением p2(z) ).
Матрица потерь, соответствующая функции (18,1), и введенные наименования для состояний природы, действий статистика и ошибок представлены в табл. 4.3.
Введем обозначение 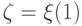 для априорной вероятности
первого состояния природы, т.е. примем, что
для априорной вероятности
первого состояния природы, т.е. примем, что
 |
( 18.2) |

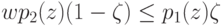
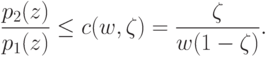 |
( 18.3) |
Условие (18,3) выделяет точки 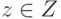 , которым
сопоставляется решение az=1, определяемое байесовской решающей
функцией
, которым
сопоставляется решение az=1, определяемое байесовской решающей
функцией  . При этом az=2, если для
соответствующего значения z условие (18,3) не выполняется.
Следовательно, байесовская стратегия
. При этом az=2, если для
соответствующего значения z условие (18,3) не выполняется.
Следовательно, байесовская стратегия  может быть задана разбиением
множества исходов Z из (17.7) на
подмножества Q1 и Q2 из (17.3),
где
может быть задана разбиением
множества исходов Z из (17.7) на
подмножества Q1 и Q2 из (17.3),
где
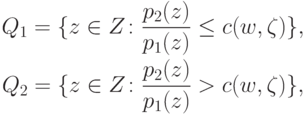 |
( 18.4) |
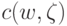 из (18.3).
из (18.3).Определение 4.1 ( критической области критерия).
Для именования стратегий (или решающих функций) статистика используется
также и более старый термин статистический
критерий (или просто критерий). При этом множество Q1
исходов  , наблюдение которых ведет к отвержению нуль-гипотезы в соответствии с некоторым критерием
, наблюдение которых ведет к отвержению нуль-гипотезы в соответствии с некоторым критерием 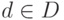 , называется критической областью
этого критерия
, называется критической областью
этого критерия
Заметим, что в силу принятого условия n=2, разбиение множества исходов Z на подмножества из (17.13) содержит лишь два элемента Q1 и Q2, т.е.
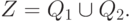 |
( 18.5) |
 полностью
определяет соответствующий критерий
полностью
определяет соответствующий критерий  .
.В дальнейшем для выделения критических областей, соответствующих
байесовским критериям 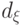 ,
,  , будем
обозначать определяющие их критические области из (18.3)
символом
, будем
обозначать определяющие их критические области из (18.3)
символом 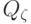 , где
, где  из (18.2).
из (18.2).
Замечание 4.3. (о проверках по отношению правдоподобия ).
Отношение вероятностей p2(z) и p1(z) из левой части правила (18.3) называют отношением правдоподобия, поскольку сами эти вероятности, характеризующие частоты исходов испытаний, первоначально именовались функциями правдоподобия. Поэтому правила выбора решений, основанные на условиях типа (18.3), получили название проверок по отношению правдоподобия.
Идея использования отношений правдоподобия для выбора простой гипотезы
(при простой альтернативе) путем сравнения этого отношения с некоторой
положительной константой c возникла независимо от концепции
байесовских решений, минимизирующих ожидаемые потери. В ее основе лежит
простое соображение, согласно которому при p2(z)/p1(z)<1
более правдоподобно, что исход 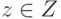 соответствует
случайной величине с распределением p1(z). При этом, учитывая
разный характер последствий, связанных с различными ошибочными решениями,
а также (обычно имеющееся) различие частот появления состояний
соответствует
случайной величине с распределением p1(z). При этом, учитывая
разный характер последствий, связанных с различными ошибочными решениями,
а также (обычно имеющееся) различие частот появления состояний 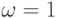 и
и 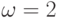 ,
значение константы сравнения c могло быть выбрано отличным от 1.
,
значение константы сравнения c могло быть выбрано отличным от 1.
Таким образом, байесовский критерий 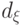 , задаваемый
критической областью
, задаваемый
критической областью 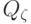 из (18.4), относится к классу
проверок по отношению правдоподобия.
При этом рассмотренный байесовский подход позволяет дать содержательную
интерпретацию значений константы
из (18.4), относится к классу
проверок по отношению правдоподобия.
При этом рассмотренный байесовский подход позволяет дать содержательную
интерпретацию значений константы  .
.
Поскольку при любой функции потерь вида (18.1)
значение величины  из (18.3)
пробегает весь диапазон
из (18.3)
пробегает весь диапазон  при изменении вероятности
при изменении вероятности  от нулевого до единичного значений, то класс всех
проверок по отношению правдоподобия совпадает с классом всех байесовских критериев
от нулевого до единичного значений, то класс всех
проверок по отношению правдоподобия совпадает с классом всех байесовских критериев 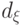 ,
, 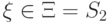 .
.


 }
}