Теорема 3.1. Существует единственная функция  из (14.18), определенная для всех задач о сделках,
задаваемых тройками (S,u*,v*) и удовлетворяющих
аксиомам (14.15)-(14.17), (14.19), (14.21), (14.22). При этом предполагается,
что хотя бы для одной пары (u,v) из замкнутого,
ограниченного и выпуклого множества S, входящего в определение задачи, справедливо (может быть
нестрогое) доминирование
из (14.18), определенная для всех задач о сделках,
задаваемых тройками (S,u*,v*) и удовлетворяющих
аксиомам (14.15)-(14.17), (14.19), (14.21), (14.22). При этом предполагается,
что хотя бы для одной пары (u,v) из замкнутого,
ограниченного и выпуклого множества S, входящего в определение задачи, справедливо (может быть
нестрогое) доминирование
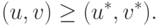 |
(
15.1)
|
Доказательство теоремы опирается на следующие леммы.
Лемма 3.1. Если множество S содержит точку (u,v), такую, что
 |
(
15.2)
|
(15.1)
является строгим, то функция
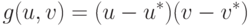 |
(
15.3)
|
 |
(
15.4)
|

.
Доказательство
Поскольку функция (15.3) является непрерывной, а непустое множество (15.4) -
ограниченным и замкнутым, то существует максимум
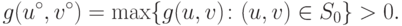 |
(
15.5)
|
Правое
неравенство в (15.5) является следствием условий (15.2)
и определений (15.3), (15.4).
Допустим, что существует еще одна точка (u',v'),
максимизирующая функцию g на S0. Тогда
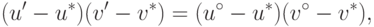 |
(
15.6)
|
откуда, учитывая (15.2), получаем
отношение:
Поскольку точки  и
и 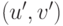 являются (по предположению) различными, то из (15.6) вытекают следствия:
являются (по предположению) различными, то из (15.6) вытекают следствия:
 |
(
15.7)
|
Из выпуклости множества S0 следует справедливость включения
Покажем, что для точки
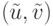
имеет
место неравенство
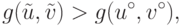 |
(
15.8)
|
противоречащее определению точки

из (15.5), что доказывает единственность точки максимума функции
g.
Действительно,
откуда, согласно (15.6) и (15.7), следует справедливость утверждения (15.8),
противоречащего (15.5).
В дальнейшем мы покажем, что условия (15.5) определяют функцию  из (14.18),
и опишем графический прием для определения аргумента
из (14.18),
и опишем графический прием для определения аргумента  из левой части (15.5).
из левой части (15.5).
Лемма 3.2. Пусть выполняются условия (15.2) и точка  удовлетворяет
определению (15.5). Тогда множество
удовлетворяет
определению (15.5). Тогда множество  лежит под прямой линией, определяемой уравнением
лежит под прямой линией, определяемой уравнением
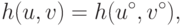 |
(
15.9)
|
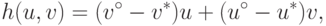 |
(
15.10)
|

,
т.е.
Доказательство. Допустим, что прямая (15.9)
не является опорной для множества S в точке  .
Тогда существует такая точка
.
Тогда существует такая точка 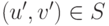 , что
, что
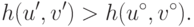 |
(
15.11)
|
Построим выпуклую линейную комбинацию:
которая принадлежит множеству

в силу его выпуклости.
Поскольку
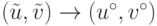
при
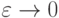
и, согласно правому неравенству
в (15.5),
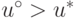
, то при достаточно малых значениях
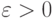
справедливо включение
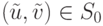
.
Теперь покажем, что при достаточно малых значениях 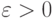 имеет место
неравенство
имеет место
неравенство 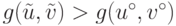 ,
противоречащее определению (15.5). Действительно,
,
противоречащее определению (15.5). Действительно,
где, согласно (15.11), коэффициент при

является положительным, а член, содержащий
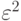
, -
пренебрежимо малым при
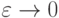
.
Следовательно, прямая линия (15.9)
является опорной к множеству
S в точке

.
 из (14.18), определенная для всех задач о сделках,
задаваемых тройками (S,u*,v*) и удовлетворяющих
аксиомам (14.15)-(14.17), (14.19), (14.21), (14.22). При этом предполагается,
что хотя бы для одной пары (u,v) из замкнутого,
ограниченного и выпуклого множества S, входящего в определение задачи, справедливо (может быть
нестрогое) доминирование
из (14.18), определенная для всех задач о сделках,
задаваемых тройками (S,u*,v*) и удовлетворяющих
аксиомам (14.15)-(14.17), (14.19), (14.21), (14.22). При этом предполагается,
что хотя бы для одной пары (u,v) из замкнутого,
ограниченного и выпуклого множества S, входящего в определение задачи, справедливо (может быть
нестрогое) доминирование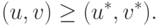

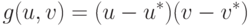

 .
.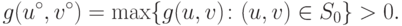
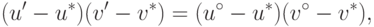
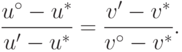
 и
и 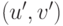 являются (по предположению) различными, то из (15.6) вытекают следствия:
являются (по предположению) различными, то из (15.6) вытекают следствия:
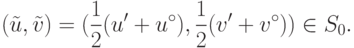
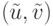 имеет место неравенство
имеет место неравенство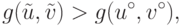
 из (15.5), что доказывает единственность точки максимума функции g.
Действительно,
из (15.5), что доказывает единственность точки максимума функции g.
Действительно,![\begin{gathered}
g(\tilde{u}, \tilde{v}) = \frac{1}{4}\left[(u' - u^\ast) +
(u^\circ - u^\ast)\right]\left[(v' - v^\ast) + (v^\circ -
v^\ast)\right]=\\ = \frac{1}{2}(u' - u^\ast)(v' - v^\ast) +
\frac{1}{2}(u^\circ -
u^\ast)(v^\circ - v^\ast) + \frac{1}{4}(u^\circ - u')(v' - v^\circ),
\end{gathered}](/sites/default/files/tex_cache/faf21a9fe868f92ddc21efc5d6e6dd27.png)
 из (14.18),
и опишем графический прием для определения аргумента
из (14.18),
и опишем графический прием для определения аргумента  из левой части (15.5).
из левой части (15.5). удовлетворяет
определению (15.5). Тогда множество
удовлетворяет
определению (15.5). Тогда множество  лежит под прямой линией, определяемой уравнением
лежит под прямой линией, определяемой уравнением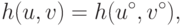
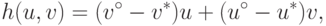
 , т.е.
, т.е.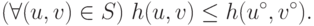
 .
Тогда существует такая точка
.
Тогда существует такая точка 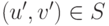 , что
, что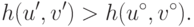
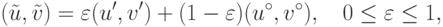
 в силу его выпуклости.
Поскольку
в силу его выпуклости.
Поскольку 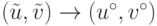 при
при 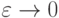 и, согласно правому неравенству
в (15.5),
и, согласно правому неравенству
в (15.5), 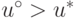 , то при достаточно малых значениях
, то при достаточно малых значениях 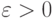 справедливо включение
справедливо включение 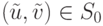 .
.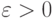 имеет место
неравенство
имеет место
неравенство 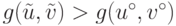 ,
противоречащее определению (15.5). Действительно,
,
противоречащее определению (15.5). Действительно,![\begin{multiline*}
g(\tilde{u}, \tilde{v}) = [u^\circ + \varepsilon(u' - u^\circ) - u^\ast]
[v^\circ + \varepsilon(v' - v^\circ) - v^\ast]) =\\
= (u^\circ - u^\ast)(v^\circ - v^\ast) +
\varepsilon^2(u' - u^\circ)(v' - v^\circ) + \\
+\varepsilon[(v^\circ - v^\ast)
(u' - u^\circ) + (u^\circ - u^\ast)(v' - v^\circ)],
\end{multiline*}](/sites/default/files/tex_cache/4416884bab88fdde017ac932fdd7b604.png)
 является положительным, а член, содержащий
является положительным, а член, содержащий 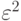 , -
пренебрежимо малым при
, -
пренебрежимо малым при 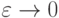 .
Следовательно, прямая линия (15.9)
является опорной к множеству S в точке
.
Следовательно, прямая линия (15.9)
является опорной к множеству S в точке  .
.
