| ВКР |
Стратегическое равновесие в 2 x 2 играх
Стратегическое равновесие при неантагонистических интересах сторон
Пусть интересы сторон, описываемые матрицами  биматричной игры,
являются неантагонистическими. С этим предположением продолжим
обсуждение поведения игроков, которое характеризуется
стратегическими парами (x*,y*), обладающими свойствами
равновесия по Нэшу (т.е. отвечающими условиям (10.10), (10.11)).
биматричной игры,
являются неантагонистическими. С этим предположением продолжим
обсуждение поведения игроков, которое характеризуется
стратегическими парами (x*,y*), обладающими свойствами
равновесия по Нэшу (т.е. отвечающими условиям (10.10), (10.11)).
Начнем со случая, когда  биматричная игра
имеет единственное
устойчивое решение и оно достигается
в смешанных стратегиях из (11.1). При этом:
биматричная игра
имеет единственное
устойчивое решение и оно достигается
в смешанных стратегиях из (11.1). При этом:
 |
( 11.11) |
 |
( 11.12) |
Пример 2.5 (неантагонистическая конкуренция). Пусть два конкурирующих фермера P1 и P2 специализируются на выращивании и продаже с автофургонов некоторой скоропортящейся продукции (например, свежей клубники). Продажа осуществляется (каждым фермером) ежедневно в одном из двух расположенных далеко друг от друга населенных пунктов П1 и П2, причем продукт, доставленный в один из этих пунктов, нецелесообразно перебрасывать в другой в силу значительной потери качества при длительной перевозке.
Если фермеры завезут товар в разные пункты, то он будет продан каждым из них. Полезность такого исхода для каждой из сторон примем за две единицы. В случае, когда автофургоны обоих фермеров одновременно окажутся в одном и том же пункте, спрос на товар, существующий в этом пункте, будет удовлетворен в основном за счет более качественного товара, доставленного первым фермером. Полезность такого исхода первый фермер оценивает как три единицы. Оценка включает как доход от продажи товара, так и получение рекламных преимуществ, открывающих перспективы полного захвата рынка в обоих пунктах (и соответствующего расширения производства).
Второй фермер оценивает полезность исхода, связанного с одновременной
торговлей обеих сторон в одном и том же населенном пункте, как нулевую. Матрицы, соответствующие этой  неантагонистической игре, представлены в табл. 2.7. Стратегии сторон
соответствуют выбору конкретного пункта (П1 или П2) для торговли в текущий
день.
неантагонистической игре, представлены в табл. 2.7. Стратегии сторон
соответствуют выбору конкретного пункта (П1 или П2) для торговли в текущий
день.
Очевидно, что первый фермер заинтересован торговать в том же месте, что и второй. Интересы второго фермера диктуют противоположный выбор (тем не менее, как уже было отмечено, рассматриваемая игра не является антагонистической).
| Матрица первого фермера | Стратегия второго фермера | Матрица второго фермера | Стратегия второго фермера | ||||
| П1 | П2 | П1 | П2 | ||||
| Стратегия первого фермера | П1 | 3 | 2 | Стратегия первого фермера | П1 | 0 | 2 |
| П2 | 2 | 3 | П2 | 2 | 0 | ||
Как следует из табл. 2.7, все исходы игры в чистых стратегиях не улучшаемы для обеих сторон и, следовательно, оптимальны по Парето. При этом не существует пар чистых стратегий сторон, обладающих свойством равновесия по Нэшу.
Согласно (10.6) и (10.8)

 |
( 11.13) |

Замечание 2.6 (антагонизм поведения без антагонизма интересов). Как следует из (11.11), (10.12), смешанная стратегия каждой из сторон, входящих в устойчивую пару (11.1), зависит исключительно от матрицы другой стороны (т.е. зависит от интересов другой стороны и не зависит от собственных интересов). Рассмотрим эту зависимость более детально.
Согласно (11.1) и (11.11),
стратегия (y*,1-y*) игрока P2 в  биматричной игре совпадает со смешанной минимаксной стратегией (11.8)
второго игрока в антагонистической игре с левой матрицей
из табл. 2.6. Т.е. действия P2,
соответствующие устойчивой паре, направлены на
уменьшение выигрыша первого игрока, а не на увеличение
собственного выигрыша.
биматричной игре совпадает со смешанной минимаксной стратегией (11.8)
второго игрока в антагонистической игре с левой матрицей
из табл. 2.6. Т.е. действия P2,
соответствующие устойчивой паре, направлены на
уменьшение выигрыша первого игрока, а не на увеличение
собственного выигрыша.
Аналогична направленность действий стороны P1. Инвертируя знаки всех элементов в правой таблице из табл. 2.6, получим матрицу

Максиминная стратегия первого игрока в антагонистической игре с такой матрицей имеет вид:
 |
( 11.14) |
Продолжим обсуждение характера равновесных решений в биматричной игре, допустив, что, наряду с устойчивыми решениями в смешанных стратегиях, существуют также устойчивые (по Нэшу) стратегические решения в чистых стратегиях.
Пример 2.6 (выбор пункта для строительства с долевым участием). Две фирмы P1 и P2 планируют строительство (с долевым участием) гостиничного комплекса в одном из двух районов города (Р1 и Р2). Фирма P1 заинтересована строить комплекс в районе Р1, где у нее есть ряд предприятий обслуживания, которые могли бы принести (в этом случае) дополнительный доход. Фирма P1 не имеет таких предприятий в районе Р2. Но именно в этом втором районе расположены точки обслуживания, созданные фирмой P2, которая (по этой причине) заинтересована в том, чтобы комплекс строился в районе P2.
| Матрица P1 | Стратегия P2 | Матрица P2 | Стратегия P2 | ||||
| P1 | P2 | P1 | P2 | ||||
| Стратегия P1 | P1 | 2 | 0 | Стратегия P1 | P1 | 1 | 0 |
| P2 | 0 | 1 | P2 | 0 | 2 | ||
Ни одна из фирм не имеет достаточных свободных средств, чтобы построить комплекс в одиночку. Поэтому, если фирмы не смогут прийти к согласию относительно района строительства, то стройка окажется невозможной. Полезность такого исхода является нулевой для каждой фирмы. Матрицы описанной игры1Приведенный пример имеет и другие известные в литературе интерпретации: "семейный спор" (Льюс Р.Д., Райфа Х. Игры и решения. - М.: ИЛ, 1961), "вежливые водители" (Мулен Э. Теория игр с примерами из математической экономики. - М.: Мир, 1985) и др. представлены в табл. 2.8.
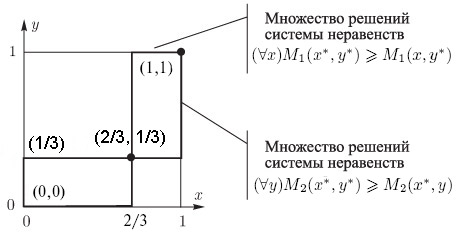
Из данных табл. 2.8 и выражений (10.6), (10.8), (10.9), (10.20) получаем, что

Смешанные стратегии, соответствующие этим парам, и отвечающие им математические ожидания M1(x*,y*), M2(x*, y*) выигрыша сторон представлены в табл. 2.9.
Отметим, что (неэффективная) равновесная пара смешанных стратегий из третьей строки табл. 2.9, соответствующая описанному выше антагонизму поведения без антагонизма интересов, может быть естественным образом интерпретирована, если выбор сторон является повторяющимся.
| (x*,y*) | (x*,1-x*) | (y*,1-y*) | M1(x*,y*) | M2(x*,y*) | Эффективность |
| (0,0) | (0,1) | (0,1) | 1 | 2 | Есть |
| (1,1) | (1,0) | (1,0) | 2 | 1 | Есть |
 |
 |
 |
 |
 |
Нет |
Такая ситуация возможна, например, если стороны последовательно (по мере накопления свободных средств) создают систему небольших гостиничных комплексов. В этом случае рассмотренная задача выбора одного из двух районов строительства будет повторяться, и математическое ожидание выигрыша можно интерпретировать как средний выигрыш (в расчете на одну партию игры) в серии последовательно решаемых задач. Однако рассмотрение такой повторяющейся игры допускает и другие подходы. Возможно планирование всей серии выборов, а не единичного акта принятия решения по строительству одного гостиничного комплекса.
Есть еще одно обстоятельство, которое следует отметить. Рассмотренный пример демонстрирует существование трех стратегических пар, обладающих свойствами равновесия по Нэшу, и при этом каждая оперирующая сторона имеет различные выигрыши во всех этих парах. Это существенно отличает рассматриваемый неантагонистический случай от антагонистических конфликтов (ср. с утверждениями следствия из теоремы о необходимых и достаточных условиях существования седловой точки ядра антагонистической игры см. "Принцип максимина и устойчивость решений в антагонистических конфликтах" ).
Кроме того, реализация любой из устойчивых пар стратегий требует согласования действий сторон. Действительно, например, если игрок P1 выберет чистую стратегию i*=2, являющуюся компонентой первой устойчивой пары из табл. 2.9, а игрок P2 выберет чистую стратегию {j*=1}, а иявляющуюся компонентой второй устойчивой пары, то такой совместный выбор не обладает свойствами поведения в равновесии. Таким образом, в конфликтах с неантагонистическими интересами сторон анализ устойчивости решений может оказаться недостаточным для выработки удовлетворительных схем поведения этих сторон. Мы вернемся к обсуждению этого вопроса в следующей лекции.