| ВКР |
Стратегическое равновесие в 2 x 2 играх
Смешанные расширения m x n биматричных игр
Рассмотренная выше схема выбора поведения, основанная на (искусственном)
внесении неопределенности путем использования случайных механизмов, может
быть обобщена на случай, когда число чистых стратегий каждой из сторон
превышает две. При таком подходе первая сторона P1 использует
рулетку, которая имеет m исходов, характеризуемых вероятностями
наступления xi,  , а вторая сторона
- рулетку с n исходами, характеризуемыми вероятностями
наступления yj,
, а вторая сторона
- рулетку с n исходами, характеризуемыми вероятностями
наступления yj,  . При
этом m и n есть числа чистых
стратегий, имеющихся соответственно у первой и второй сторон. Теперь
введем следующее определение.
. При
этом m и n есть числа чистых
стратегий, имеющихся соответственно у первой и второй сторон. Теперь
введем следующее определение.
Определение 2.5. Смешанными стратегиями
игроков P1 и P2 в  биматричной
игре соответственно называются векторы
биматричной
игре соответственно называются векторы
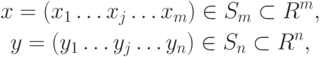
 |
( 11.15) |
Поскольку в классе Sm смешанных стратегий2Многомерные
фигуры, обладающие свойствами (11.15), называются симплексами .}
стороны P1 для любого номера i,  , существует стратегия x(i), удовлетворяющая условиям
, существует стратегия x(i), удовлетворяющая условиям
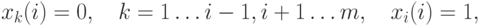
 .
.Выбор игроками P1 и P2 смешанных стратегий 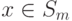 и
и 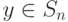 еще не определяет конкретного исхода игры.
В связи с этим, в качестве оценок эффективности M1(x, y) и M2(x,y),
которую обеспечивает игрокам выбор пары (x,y), принимаются математические ожидания
еще не определяет конкретного исхода игры.
В связи с этим, в качестве оценок эффективности M1(x, y) и M2(x,y),
которую обеспечивает игрокам выбор пары (x,y), принимаются математические ожидания
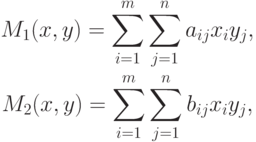 |
( 11.16) |
Если принять, что x и y есть векторы-столбцы,
и обозначить матрицы, представляющие выигрыши первого и второго
игроков (при игре в чистых стратегиях), соответственно
через A и B, то, согласно (11.16), смешанное расширение  биматричной игры можно
представить следующей моделью
(в нормальной форме):
биматричной игры можно
представить следующей моделью
(в нормальной форме):
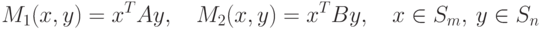 |
( 11.17) |
Для произвольной  биматричной игры справедливо
утверждение, что в ее смешанном расширении существует хотя бы одна ситуация
равновесия (по Нэшу). Т.е. в смешанном расширении каждой биматричной
игры существует пара смешанных стратегий ( x*,y*),
удовлетворяющая неравенствам (3.3),
где X=Sm и Y=Sn.
В случае, когда интересы сторон являются противоположными
(антагонистическими), это утверждение подразумевает существование
седловой точки (x*,y*) ядра
биматричной игры справедливо
утверждение, что в ее смешанном расширении существует хотя бы одна ситуация
равновесия (по Нэшу). Т.е. в смешанном расширении каждой биматричной
игры существует пара смешанных стратегий ( x*,y*),
удовлетворяющая неравенствам (3.3),
где X=Sm и Y=Sn.
В случае, когда интересы сторон являются противоположными
(антагонистическими), это утверждение подразумевает существование
седловой точки (x*,y*) ядра
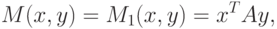 |
( 11.18) |
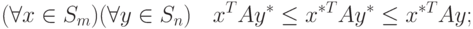 |
( 11.19) |
Существование пар стратегий, удовлетворяющих условиям (11.9)
и, следовательно, являющихся равновесными решениями для смешанных расширений  антагонистических игр, которые имеют ядра вида (11.18)
(с любыми матрицами A ), будет показано в следующем параграфе.
Доказательство упомянутого выше факта
разрешимости условий (6.3) для смешанного расширения (11.17)
любой
антагонистических игр, которые имеют ядра вида (11.18)
(с любыми матрицами A ), будет показано в следующем параграфе.
Доказательство упомянутого выше факта
разрешимости условий (6.3) для смешанного расширения (11.17)
любой  биматричной игры может быть найдено в других источниках3См., например: Оуэн Г. Теория игр. - М.: Мир, 1971..
Мы опускаем это доказательство в нашей небольшой (соответствующей
программе вводного курса) книге, поскольку для общего
биматричной игры может быть найдено в других источниках3См., например: Оуэн Г. Теория игр. - М.: Мир, 1971..
Мы опускаем это доказательство в нашей небольшой (соответствующей
программе вводного курса) книге, поскольку для общего  случая (в отличие от уже рассмотренных
случая (в отличие от уже рассмотренных  задач) оно не дает способа
вычисления пары стратегий, порождающих ситуацию равновесия (т.е. оно не
является конструктивным ).
Кроме того, как уже было отмечено,
анализ устойчивости в таких задачах может оказаться недостаточным
для выработки удовлетворительных схем поведения сторон.
задач) оно не дает способа
вычисления пары стратегий, порождающих ситуацию равновесия (т.е. оно не
является конструктивным ).
Кроме того, как уже было отмечено,
анализ устойчивости в таких задачах может оказаться недостаточным
для выработки удовлетворительных схем поведения сторон.

