| ВКР |
Смешанные стратегии и проблема устойчивости решений
При 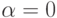 множество пар вида
множество пар вида 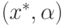 , 0<x*<1,
совпадает с нижней
стороной квадрата D (см. левый и правый фрагменты третьего ряда на
рис. 2.8).
, 0<x*<1,
совпадает с нижней
стороной квадрата D (см. левый и правый фрагменты третьего ряда на
рис. 2.8).
При  и A>0 решениям соответствует
правая сторона квадрата D, а при A<0 - левая сторона
этого квадрата. Такие решения уже рассматривались (их образы представлены на
верхних фрагментах рис. 2.8).
и A>0 решениям соответствует
правая сторона квадрата D, а при A<0 - левая сторона
этого квадрата. Такие решения уже рассматривались (их образы представлены на
верхних фрагментах рис. 2.8).
Случай 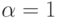 , когда множество пар вида
, когда множество пар вида 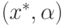 , 0<x*< 1, совпадает с верхней стороной
квадрата D, представлен
нижними фрагментами на рис. 2.8. При
, 0<x*< 1, совпадает с верхней стороной
квадрата D, представлен
нижними фрагментами на рис. 2.8. При  получаем те же
решения, что и на верхних фрагментах рис. 2.8 (левый фрагмент - при A>0 и правый фрагмент - при A<0 ).
получаем те же
решения, что и на верхних фрагментах рис. 2.8 (левый фрагмент - при A>0 и правый фрагмент - при A<0 ).
2. Аналогично определяется множество
всех пар 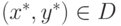 , удовлетворяющих неравенствам (10.13),
которые эквивалентны условиям (10.11). Результаты
этого анализа представлены на рис. 2.9.
, удовлетворяющих неравенствам (10.13),
которые эквивалентны условиям (10.11). Результаты
этого анализа представлены на рис. 2.9.
В случае, когда для значений b и B из (10.8)
справедливо, что b=B=0, решениями неравенств (10.11)
являются все точки квадрата D. Отмеченная
на рисунке величина  определяется выражением
определяется выражением
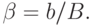 |
( 10.20) |
Заметим, что эти результаты можно вывести и из рис. 2.8, если изменить нумерацию игроков (при этом первый игрок становится вторым, а второй - первым), транспонировать их матрицы и поменять местами величины x* и y*.
3. Как следует из проведенной классификации (см. рис. 2.8), в зависимости от значений коэффициентов a и A из (10.6) множество решений системы (10.10) либо включает хотя бы одну из боковых сторон квадрата D, либо включает трехзвенную ломаную линию, соединяющую концы одной из диагоналей квадрата.
Аналогично (см. рис. 2.9), в зависимости от значений коэффициентов b и B из (10.8), множество решений системы (10.11) либо включает одну из горизонтальных сторон квадрата D, либо включает ломаную ( трехзвенную ) линию, соединяющую концы одной из диагоналей этого квадрата.
Покажем, что в любом из этих четырех случаев существует хотя бы одна пара (x*,y*), являющаяся решением одновременно для обеих
систем неравенств (10.10), (10.11) и, следовательно,
представляющая собой устойчивое
решение смешанного расширения (10.9) исходной  биматричной игры.
биматричной игры.
Пусть решения систем (10.10) и (10.11) включают стороны квадрата D. Тогда они имеют общую точку, являющуюся вершиной этого квадрата, ибо любая боковая и любая горизонтальная стороны квадрата пересекаются в какой-либо его вершине. Левый фрагмент на рис. 2.10 иллюстрирует один из обсуждаемых случаев (A=0,a>0,B=0,b<0 ).
Рассмотрим случай, когда решения систем (10.10)
и (10.11) включают ломаные линии, соединяющие концы диагоналей
квадрата. Как следует из рис. 2.8 и рис. 2.9 (см. фрагменты, расположенные
во вторых (сверху) рядах), эти монотонные линии необходимо пересекаются
в некоторой внутренней точке квадрата (независимо от того, соединяют ли обе
ломаные линии концы одной и той же диагонали или концы разных диагоналей).
Средний фрагмент на рис. 2.10 представляет возможный случай такого рода
( 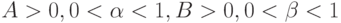 ).
).
Пусть теперь множество решений одной из систем (10.10),
(10.11) включает сторону квадрата D, а решение
другой системы - трехзвенную ломаную линию, соединяющую концы некоторой
диагонали этого квадрата. Тогда одна из вершин является решением для обеих
систем (10.10), (10.11), ибо каждая
сторона квадрата имеет общую вершину с каждой его диагональю. Случай
такого рода представлен правым фрагментом на рис. 2.10
( 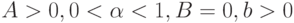 ).
).




