| ВКР |
Смешанные стратегии и проблема устойчивости решений
Существование устойчивых решений в смешанных расширениях 2 x 2 игр
Обобщим результаты рассмотрения конкретного примера на случай смешанного
расширения произвольной  биматричной игры. Обозначим
элементы матриц первой и второй сторон соответственно через aij}
и bij
биматричной игры. Обозначим
элементы матриц первой и второй сторон соответственно через aij}
и bij  . Примем, что сторона P1
использует смешанную стратегию (x,1-x),
. Примем, что сторона P1
использует смешанную стратегию (x,1-x), 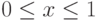 ,
а сторона P2 - смешанную стратегию (y,1-y),
,
а сторона P2 - смешанную стратегию (y,1-y), 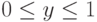 .
Смешанные стратегии (x,1-x), (y,1-y), выбранные сторонами P1, P2, однозначно описываются парой вещественных чисел (x,y), принадлежащей единичному квадрату
.
Смешанные стратегии (x,1-x), (y,1-y), выбранные сторонами P1, P2, однозначно описываются парой вещественных чисел (x,y), принадлежащей единичному квадрату
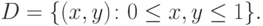 |
( 10.4) |
Математическое ожидание M1(x,y) выигрыша стороны P1, соответствующее паре (x,y) (с учетом независимости выборов, порождаемых рулетками сторон), определяется выражением
![\begin{gathered}
M_1 (x,y) = [a_{11} x + a_{21}(1 - x)]y + [a_{12}x + a_{22}(1 - x)](1-
y)=\\ = xy (a_{11} - a_{12} - a_{21} + a_{22}) - x(a_{22} - a_{12}) -
y(a_{22} - a_{21}) + a_{22},
\end{gathered}](/sites/default/files/tex_cache/1cce0438f6d054ad9a6daa42708af11b.png)
 |
( 10.5) |
 |
( 10.6) |
Аналогичные вычисления дают выражение для математического ожидания M2(x,y) выигрыша стороны P2:
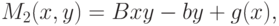 |
( 10.7) |
 |
( 10.8) |

| Матрица игрока P1 | Смешанная cтратегия P2 | Матрица игрока P2 | Смешанная cтратегия P2 | ||||
| y | 1-y | y | 1-y | ||||
| Смешанная стратегия P1 | x | a11 | a12 | Смешанная стратегия P1 | x | b11 | b12 |
| 1-x | a21 | a22 | 1-x | b21 | b22 | ||
Теперь вопрос о существовании пары (x*,y*), определяющей устойчивое (по Нэшу) решение (x*,1-x*), (y*,1-y* ) в смешанном расширении
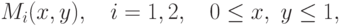 |
( 10.9) |
 биматричной игры, сводится к вопросу о
существовании
решения
биматричной игры, сводится к вопросу о
существовании
решения  системы неравенств:
системы неравенств:![(\forall x \in [0,1])\, M_1 (x^\ast, y^\ast) \ge M_1(x, y^\ast),](/sites/default/files/tex_cache/c6d1802a3a9be55681e419fd9d432f98.png) |
( 10.10) |
![(\forall y \in [0,1])\, M_2 (x^\ast, y^\ast) \ge M_2(x^\ast, y).](/sites/default/files/tex_cache/bf3eb05bc31824ba8f8074ae16e54a49.png) |
( 10.11) |
Лемма 2.1. Для выполнения соответствующего паре (x*,y*) континуума неравенств (10.10) необходима и достаточна справедливость двух неравенств:
 |
( 10.12) |
 |
( 10.13) |
Доказательство Покажем эквивалентность условий (10.10) и (10.12). Эквивалентность условий (10.11) и (10.13) доказывается аналогично. Подстановка значений x=0 и x=1 в условия (10.10) дает неравенства (10.12). Т.е. необходимость отношений (10.12) действительно имеет место.
Пусть выполняются условия (10.12).
Из линейности по x выражения (10.5)
для величины M1(x,y) следует, что при любом
значении ![x \in [0, 1]](/sites/default/files/tex_cache/93f30fd332c4e8fea09e07b515abcd4a.png)
![M_1(x, y^\ast) = M_1[1 \cdot x + 0 \cdot (1 - x), y^\ast] =
x M_1 (1, y^\ast) + (1 - x)M_1(0, y^\ast).](/sites/default/files/tex_cache/8fe5a3b75f482489e68615abfd42db91.png)
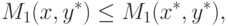
Теорема 2.2 (о существовании устойчивых решений в смешанном
расширении  биматричной игры. Каждая
биматричной игры. Каждая  биматричная игра имеет устойчивое (по Нэшу)
решение в смешанных стратегиях.
биматричная игра имеет устойчивое (по Нэшу)
решение в смешанных стратегиях.
Доказательство 1. Определим множество всех пар  , удовлетворяющих неравенствам (10.12),
которые, согласно доказанной лемме,
эквивалентны условиям (10.10).
, удовлетворяющих неравенствам (10.12),
которые, согласно доказанной лемме,
эквивалентны условиям (10.10).
При x=0 из выражения (10.5) и из первого неравенства в (10.12) следует справедливость отношения
 |
( 10.14) |
Аналогично, из второго неравенства в (10.12) (для случая x=1 ) вытекает оценка
 |
( 10.15) |
Найдем множество всех решений системы (10.14), (10.15), лежащих в единичном квадрате D из (10.4).
При x*=0 условие (10.14) необходимо выполняется и, следовательно, все пары вида
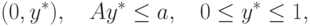 |
( 10.16) |
Аналогично, при x*=1 необходимо выполняется условие (10.15) и все пары вида
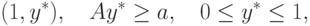 |
( 10.17) |
Наконец, при 0<x*<1 множество решений системы (10.14), (10.15) состоит из пар вида
 |
( 10.18) |
Теперь рассмотрим выполнимость полученных
условий (10.16)-(10.18) в зависимости от значений
величин a и A из (10.06).
При a=A=0 любая пара  удовлетворяет условиям (10.16)-(10.18)
и, следовательно, является решением (10.10).
удовлетворяет условиям (10.16)-(10.18)
и, следовательно, является решением (10.10).
При A=0 и  возможны два случая, которым
соответствуют два
верхних фрагмента на рис. 2.8. При a>0
все точки, лежащие на левой
стороне (выделена жирной линией на левом верхнем фрагменте)
квадрата D, являются решениями системы (10.10).
При a<0 этим свойством обладают все точки, лежащие на
правой стороне квадрата D (см. правый верхний
фрагмент на рис. 2.8).
возможны два случая, которым
соответствуют два
верхних фрагмента на рис. 2.8. При a>0
все точки, лежащие на левой
стороне (выделена жирной линией на левом верхнем фрагменте)
квадрата D, являются решениями системы (10.10).
При a<0 этим свойством обладают все точки, лежащие на
правой стороне квадрата D (см. правый верхний
фрагмент на рис. 2.8).
Пусть 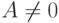 . Тогда, согласно (10.16),
все решения вида
. Тогда, согласно (10.16),
все решения вида 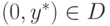 возможны лишь
при условии, что
возможны лишь
при условии, что  (если A>0 )
или
(если A>0 )
или  (если A<0 ), где
(если A<0 ), где
 |
( 10.19) |
Аналогично, из (10.17) выводим, что все решения вида 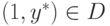 возможны лишь при выполнении
условия
возможны лишь при выполнении
условия  (если A>0 ) или при
выполнении условия
(если A>0 ) или при
выполнении условия  (если A<0 ).
Наконец, согласно (10.18),
решения вида
(если A<0 ).
Наконец, согласно (10.18),
решения вида  , 0<x*<1,
возможны лишь в случаях, когда
, 0<x*<1,
возможны лишь в случаях, когда  .
Случаю A>0 соответствует левый
фрагмент второго (сверху) ряда на рис. 2.8. При этом все точки
из D, удовлетворяющие условиям (10.10),
лежат на жирной ломаной линии, составленной из трех
отрезков. Два вертикальных отрезка представляют точки вида (0,y*)
и (1,y*). Горизонтальный отрезок является образом точек вида
.
Случаю A>0 соответствует левый
фрагмент второго (сверху) ряда на рис. 2.8. При этом все точки
из D, удовлетворяющие условиям (10.10),
лежат на жирной ломаной линии, составленной из трех
отрезков. Два вертикальных отрезка представляют точки вида (0,y*)
и (1,y*). Горизонтальный отрезок является образом точек вида 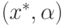 , 0<x*<1. Правый фрагмент из этого
же ряда соответствует случаю A<0,
, 0<x*<1. Правый фрагмент из этого
же ряда соответствует случаю A<0,  .
.

