НОУ ИНТУИТ | Исследование операций и модели экономического поведения. Лекция 5: Распределение информации и устойчивость решений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.04.2007 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 24 студентам

| Поделиться |

Поддержать

| Скачать электронную книгу

Симметричное распределение информации и проблема равновесия по Нэшу

Рассмотрим поведение участников рынка, представленного описанной моделью, как некоторую игру двух лиц, в которой роль первой стороны (P₁) играет потребитель, а роль второй стороны (P₂) - производитель. При этом стратегии сторон P₁ и P₂ состоят соответственно в выборе потребителем цены p_max>c из (4.10), при которой исчезает спрос на товар, и в выборе производителем параметра B>0 из (4.3).

Примем, что интересы потребителя состоят в максимизации объема товара D(p_eq), который ему удается закупить по цене p_eq, не превышая затрат E_m. Таким образом, критерий эффективности потребителя имеет вид

$M_1(p_{\max},B)=D(p_\text{eq}),\quad c<p_{\max}<\infty.$

( 4.14)

Критерий эффективности производителя в предположении, что его интересы состоят в максимизации прибыли при p=p_eq, имеет вид:

$M_2(p_{\max},B)=\pi(p_\text{eq}),\quad 0<B<\infty.$

( 4.15)

Согласно (4.6), (4.9) и (4.10),

$D(p_\text{eq})=4E_m(p_{\max}-c)B/[4E_m+B(p_{\max})^2]$

( 4.16)

и, в соответствии с (4.6), (4.11),

$\pi(p_\text{eq})=(4E_m)^2(p_{\max}-c)^2B/[4E_m+B(p_{\max})^2]^2.$

( 4.17)

Теперь из (4.16), (4.17) вытекает, что

$B\pi (p_\text{eq})=D^2(p_\text{eq}),$

( 4.18)

откуда, учитывая (4.14), (4.15), выводим равенство

$M_1(p_{\max},B)=[BM_2(p_{\max},B)]^{1/2}.$

( 4.19)

Как следует из (4.19), интересы сторон не являются ни совпадающими, ни противоположными.

Исследуем вопрос о существовании ситуации стратегического равновесия по Нэшу, считая, что стороны, осуществляющие независимо друг от друга выбор своих стратегий, располагают одинаковой информацией. Полагая параметр $B\in (0,\infty)$ заданным, определим стратегию p_max потребителя, обеспечивающую максимальную закупку D(p_eq) из (4.16). Из выражения

$\frac{dD(p_\text{eq})}{dp_{\max}}=\frac{4E_mB\left[4E_m-Bp_{\max}(p_{\max}-2c)\right]}{\left[4E_m+Bp^2_{\max}\right]^2}$

( 4.20)

следует, что при p_max} производная (4.20) имеет нулевое значение в точках плоскости (p_max,B), координаты которых удовлетворяют соотношению

$B=4E_m/p_{\max}(p_{\max}-2c).$

( 4.21)

Указанным точкам соответствует верхняя кривая на рис.1.10.

Поскольку в точках этой кривой вторая производная

$\frac{d^2D(p_\text{eq})}{dp^2_{\max}}=\frac{8E_mB^2\left[Bp^2_{\max}(p_{\max}-3c)-4E_m(3p_{\max}-c)\right]}{\left[4E_m+Bp^2_{\max}\right]^3}$

является отрицательной, то при p_max}>2c объем закупки D(p_eq) достигает максимума по p_max в точках из (4.21).

Рис. 1.10.

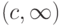При $c<p_{\max}\le 2c$ производная (4.20) является положительной. Следовательно, кривая (4.21) есть геометрическое место точек, в которых достигается максимум D(p_eq) по p_max из диапазона $(c,\infty)$ . Подставляя выражение для B из (4.21) в правую часть формулы (4.16), выводим, что объем закупки D(p_eq) в точках кривой (4.21) определяется соотношением

$D(p_\text{eq})=2E_m/p_{\max}.$

Отсюда вытекает, что объем закупки растет с уменьшением цены p_max, стремясь к величине E_m/c при $p_{\max}\to 2c$ . Стрелка, которая нанесена на верхнюю кривую, представленную на рис.1.10, указывает направление перемещения, сопровождаемого отмеченным выше ростом объема закупки.

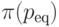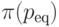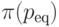Теперь определим стратегию B производителя, максимизирующую его прибыль $\pi(p_\text{eq})$ из (4.17) при заданном значении параметра $p_{\max}\in (c,\infty)$ . Согласно (4.12), (4.13), максимум $\pi(p_\text{eq})$ достигается при условии $p_\text{eq}=p_\pi$ . Из этого равенства и из определяющих его левую и правую части выражений (4.6) и (4.13) выводим, что максимальное значение прибыли $\pi(p_\text{eq})$ достигается при выполнении условия

$B=4E_m/(p_{\max})^2.$

( 4.22)

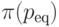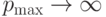Точки, удовлетворяющие указанному условию, представлены нижней кривой на рис.1.10. Значение прибыли $\pi(p_\text{eq})$ в точках этой кривой определяется выражением (4.12). Следовательно, величина $\pi(p_\text{eq})=\pi(p_\pi)$ растет с увеличением параметра p_max, приближаясь к значению E_m при $p_{\max}\to \infty$ . Указанное направление роста прибыли отмечено стрелкой на нижней кривой, изображенной на рис.1.10.

Из (4.21) и (4.22) следует, что при всех значениях $p_{\max}\in (2c,\infty)$ кривая, соответствующая первому из этих выражений, лежит выше кривой, соответствующей второму выражению. Т.е. эти кривые не имеют точек пересечения. Следовательно, в данной задаче нет стратегических пар, удовлетворяющих условиям (3.3) равновесия по Нэшу для критериев (4.14) и (4.15).

Дальше >>

Исследование операций и модели экономического поведения

Распределение информации и устойчивость решений

Симметричное распределение информации и проблема равновесия по Нэшу

Вопросы и ответы

Студенты

Авторизоваться

Исследование операций и модели экономического поведения

Распределение информации и устойчивость решений

Симметричное распределение информации и проблема равновесия по Нэшу

Вопросы и ответы

Студенты