Несимметричное распределение информации и устойчивость по Штакельбергу
Примем, что производитель (P2) адаптирует свое поведение к
условиям рынка значительно быстрее, чем изменяется поведение потребителя (P2). Т.е. производитель успевает максимизировать прибыль 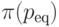 по параметру B столь быстро, что при этом стратегию pmax потребителя можно считать неизменной. Принятое допущение можно
интерпретировать как фиксирование последовательности действий сторон.
Первый ход делает потребитель, выбирая стратегию x=pmax, а
затем свой ход делает производитель, что позволяет ему выбирать стратегию y=B как функцию известного значения x=pmax.
по параметру B столь быстро, что при этом стратегию pmax потребителя можно считать неизменной. Принятое допущение можно
интерпретировать как фиксирование последовательности действий сторон.
Первый ход делает потребитель, выбирая стратегию x=pmax, а
затем свой ход делает производитель, что позволяет ему выбирать стратегию y=B как функцию известного значения x=pmax.
При сделанных предположениях производитель имеет возможность использовать
стратегию-функцию y*(x)=B*(pmax), максимизирующую
его критерий-прибыль из 4.15, т.е. обеспечивающую выполнение условия
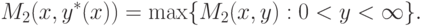 |
(
4.23)
|
Все возможные при таком поведении стратегические пары
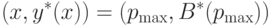 |
(
4.24)
|
необходимо удовлетворяют равенству (4.22),
поскольку оно определяет
значение параметра
B, доставляющее
максимум критерию
M2 при заданном
значении параметра
pmax. Следовательно, выбор потребителем стратегии
x=pmax определяет конкретную точку вида (4.24),
которая лежит на нижней кривой, изображенной на
рис.1.10. При
этом потребитель заинтересован в выборе стратегии
x*, которой соответствует точка указанной кривой,
характеризуемая максимальным (на кривой) значением критерия
M1
из (4.14). Т.е.
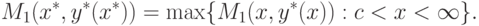 |
(
4.25)
|
Определение 1.6 ( равновесие по Штакельбергу ).
Пара стратегий (x*,y*(x*)), удовлетворяющая
условиям (4.23) и (4.25), называется
стратегической точкой равновесия по Штакельбергу . 7
Определим точку равновесия по Штакельбергу в рассматриваемом примере. Как
следует из (4.22) (с учетом введенных обозначений x=pmax и y=B ),
 |
(
4.26)
|
Далее, из (4.14) и (4.16) вытекает, что
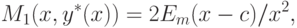 |
(
4.27)
|
причем производная по
x от этой величины обращается в ноль при
 |
(
4.28)
|
Поскольку
вторая производная от величины (4.27) в
точке (4.28) является отрицательной, то
значение 
из
правой части (4.28) обеспечивает
максимум
критерия (4.27). Следовательно, согласно (4.26)
и (4.28), точка с координатами
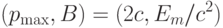 |
(
4.29)
|
соответствует ситуации
равновесия по Штакельбергу (см.
рис.1.10). При этом, как следует из (4.27) и (4.28),
 |
(
4.30)
|
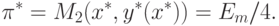 |
(
4.31)
|
В заключение сравним решение (4.29) с точкой
 |
(
4.32)
|
отмеченной темным кружком на
рис.1.10.
Согласно (4.16) и (4.17), этой точке соответствуют значения
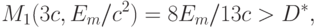 |
(
4.33)
|
 |
(
4.34)
|
где
D* и
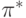
соответственно из (4.30) и (4.31).
Как следует из (4.33) и (4.34), устойчивая по Штакельбергу
точка (4.29) не является эффективным решением, поскольку ее превосходит неустойчивое решение,
определяемое точкой (4.32).
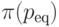 по параметру B столь быстро, что при этом стратегию pmax потребителя можно считать неизменной. Принятое допущение можно
интерпретировать как фиксирование последовательности действий сторон.
Первый ход делает потребитель, выбирая стратегию x=pmax, а
затем свой ход делает производитель, что позволяет ему выбирать стратегию y=B как функцию известного значения x=pmax.
по параметру B столь быстро, что при этом стратегию pmax потребителя можно считать неизменной. Принятое допущение можно
интерпретировать как фиксирование последовательности действий сторон.
Первый ход делает потребитель, выбирая стратегию x=pmax, а
затем свой ход делает производитель, что позволяет ему выбирать стратегию y=B как функцию известного значения x=pmax.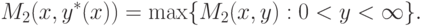
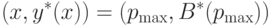
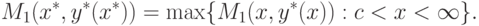

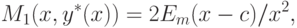

 из
правой части (4.28) обеспечивает максимум
критерия (4.27). Следовательно, согласно (4.26)
и (4.28), точка с координатами
из
правой части (4.28) обеспечивает максимум
критерия (4.27). Следовательно, согласно (4.26)
и (4.28), точка с координатами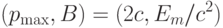

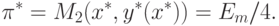

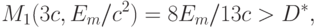

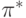 соответственно из (4.30) и (4.31).
Как следует из (4.33) и (4.34), устойчивая по Штакельбергу
точка (4.29) не является эффективным решением, поскольку ее превосходит неустойчивое решение,
определяемое точкой (4.32).
соответственно из (4.30) и (4.31).
Как следует из (4.33) и (4.34), устойчивая по Штакельбергу
точка (4.29) не является эффективным решением, поскольку ее превосходит неустойчивое решение,
определяемое точкой (4.32).
