| ВКР |
Математическая модель задачи выбора решений
Замечание 1.4 (об отложенном потреблении). Если фирма Pi не осуществляет инвестиций в освоение новых технологий (т.е., если Pi выбирает вариант xi=0 ) и использует имеющиеся средства, например, для немедленного укрепления материальной базы, обеспечивающей ведение работ традиционным способом, то уровень качества Wi(0,t) остается постоянным в течение всего периода [0,2]. При этом Wi(0,t)=1.
В случае вложения всех ресурсов в освоение новых технологий (т.е. при выборе варианта xi=1, к концу периода [0,2] достигается более высокий уровень качества Wi(1,2)=2. Однако при этом в начальный момент t=0 уровень качества остается таким же, каким он был до начала подготовки к тендеру. Это значение принято за нулевую отметку - см. рис.1.1.
В остальных случаях (т.е. при 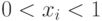 )
отрезок, представляющий график Wi(xi,t) на
рис.1.1, лежит в конусе,
образованном графиками зависимостей Wi(0,t) и Wi(1,t)=t.
Следовательно, инвестирование части средств в новые технологии, а оставшихся средств - в
укрепление технологии, использовавшейся ранее, позволяет уже в начальный
момент добиться превышения прежнего уровня качества. Это обстоятельство
может быть существенным, поскольку, как уже было отмечено, условия
конкурса предполагают, что параметр качества в любом случае должен быть не
ниже некоторого значения Wmin (см. рис.1.1).
С другой стороны, выбор положительного значения xi обеспечивает последовательное
наращивание показателя качества и гарантирует в периоде [1, 2]
превышение единичного уровня. Таким образом, при всей простоте зависимости (1.19)
она правильно (хотя и схематично) отражает роль параметра xi как показателя объема
отложенного потребления.
)
отрезок, представляющий график Wi(xi,t) на
рис.1.1, лежит в конусе,
образованном графиками зависимостей Wi(0,t) и Wi(1,t)=t.
Следовательно, инвестирование части средств в новые технологии, а оставшихся средств - в
укрепление технологии, использовавшейся ранее, позволяет уже в начальный
момент добиться превышения прежнего уровня качества. Это обстоятельство
может быть существенным, поскольку, как уже было отмечено, условия
конкурса предполагают, что параметр качества в любом случае должен быть не
ниже некоторого значения Wmin (см. рис.1.1).
С другой стороны, выбор положительного значения xi обеспечивает последовательное
наращивание показателя качества и гарантирует в периоде [1, 2]
превышение единичного уровня. Таким образом, при всей простоте зависимости (1.19)
она правильно (хотя и схематично) отражает роль параметра xi как показателя объема
отложенного потребления.
Критерии
эффективности сторон, соответствующие моменту ![t\in [0,2]](/sites/default/files/tex_cache/9f15c2e21f34e562b5319f790363a5cd.png) проведения конкурса, определяются различием уровней
качества, которые стороны могут обеспечить в этот момент, т.е.
проведения конкурса, определяются различием уровней
качества, которые стороны могут обеспечить в этот момент, т.е.
 |
( 1.20) |
Таким образом, рассмотренному примеру соответствует модель операции в
нормальной форме вида (1.13), причем роль стратегий x= x1 и y=x2 играют выбираемые сторонами объемы
ресурса, инвестированного в развитие. Момент t проведения конкурса
сторонам заранее не известен
и может интерпретироваться как состояние природы. Т.е. u=t и ![u\in [0,2]](/sites/default/files/tex_cache/6982faedb0be90a8aea0bef32a5ccf8d.png) , где, как уже отмечалось, само множество U является заданным.
, где, как уже отмечалось, само множество U является заданным.
Целью операции для каждой стороны является обеспечение максимального превосходства показателя качества, достигаемого на момент конкурса, над уровнем качества, достигаемого на тот же момент другой стороной. При этом мы будем полагать, что обеим сторонам известны как зависимости (1.19), (1.20), так и доступные объемы ресурсов X=[0,1], Y=[0,1].
Замечание 1.5 (о противоположности интересов сторон). То обстоятельство, что конкурсное соревнование уже само по себе определяет противоположность интересов сторон P1 и P2, находит свое отражение в вытекающем из (1.20) равенстве
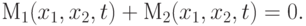 |
( 1.21) |
Заметим, что в случае, когда число сторон превышает две и допустимо объединение участников в коалиции, постоянная сумма всех критериев эффективности еще не означает противоположности интересов сторон, поскольку члены одной и той же коалиции могут находиться в кооперации, а не в противостоянии друга с другом. Следовательно, случай операции с двумя сторонами (говорят еще "с двумя лицами ") и нулевой суммой критериев является в поведенческом отношении особым.
Определение 1.3. Операции двух лиц, характеризуемые нулевой суммой критериев эффективности сторон, называются антагонистическими.
Замечание 1.6 (о пороговых критериях). Рассмотренный пример представляет собой частный случай задачи соревнования двух сторон. В задачах такого рода зачастую рассматривается не столько количественное различие достижений сторон, сколько факт превосходства показателей, достигнутых одной стороной, над показателями другой стороны. Все возможные исходы можно классифицировать как "победы", "ничьи" и "поражения". Если принять, что победам, ничьим и поражениям соответствуют оценки 2, 1 и 0 "очков", то в рассматриваемой задаче можно ввести критерий эффективности вида
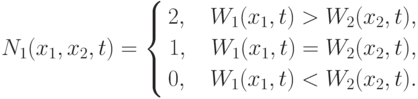 |
( 1.22) |
Критерий (1.22) относится к числу так называемых пороговых критериев (результат, достигаемый другой стороной, рассматривается как порог, который нужно превысить). Мы, однако, будем рассматривать случай, когда критерий задается условиями (1.20), полагая, что стороны (допускающие несовершенство методики оценки качества) заинтересованы в достижении максимально возможного превосходства над конкурентом.


